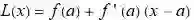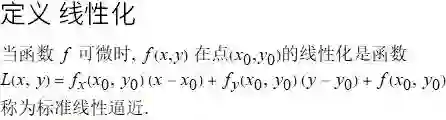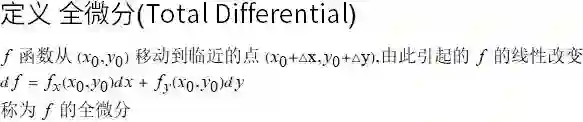【线性化和全微分】图解高等数学-下 13

11.6 线性化和微分

二元或多元函数的线性化和微分类似一元函数的线性逼近. 先来回顾下一元的公式.

二元函数的线性化

用更简单的二元函数来代替函数 f(x,y).

也就是 z=L(x,y) 是曲面f(x,y) 在点 $(x_0,y_0)$ 的切平面. 观察下面动画来查看函数 $\text{f(x,y) = -}{x}^2-y^2$ 在点 (0,0) 的线性化逼近.

从上图可以看到二元函数的线性化切平面逼近与一元函数的切线线性化逼近是非常类似的.

标准线性逼近的精确度

现在考虑逼近的精确度是如何衡量的, 这里受到三个因素的影响:

1. x 和 $x_0$ 的接近程度

2. y 和 $y_0$ 的接近程度

3. 函数 f 在点 $(x_0,y_0)$ 附近的弯曲程度(可以用二阶导数衡量)

用微分来预测变化

「予人玫瑰, 手留余香」

转发既是支持, 我们会努力走得更远!