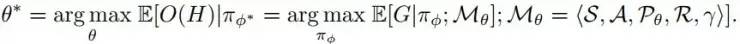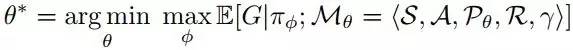首发 | 环境也能强化学习,智能体要找不着北了,UCL汪军团队提出环境设计的新方法
AI 科技评论按:提到“强化学习”,大家都知道这是一种让智能体寻找优化策略、从而与环境互动获得奖励的半监督学习方法。但是在汪军教授看来,强化学习的应用领域不止如此。
在刚刚结束的CCF-GAIR 2017大会中,来自伦敦大学学院 UCL 计算机系的汪军教授在自己的演讲 如何进行大规模多智体强化学习? - AI 科技评论 中提到了一类他们团队最近正在研究的环境设计问题,比如宜家希望自己店铺空间设计优化,优化目标可以是环境中不同位置的人流量平均,这样各个地方摆放的商品都可以兼顾到;在快递分拣的场景里,每一个洞对应一个不同的目的地,分拣机器人需要把快递投入对应的洞里,那么就希望分拣机器人的速度尽量快,这既包括行驶的总路径要尽量短,也包括路径之间的交叉要尽量少;共享单车给城市管理带来不少问题,也需要与实时需求对应,合理定价分配资源。
能够达到期望的环境是需要设计的,但是很难分析性地用标准设计方法处理这类复杂的对象与环境交互问题,对整个解空间进行穷举演算的计算成本又太高。
汪军教授在UCL的研究团队,除了教授本人以外还有正在访问UCL的北大博士生张海峰和上海交通大学张伟楠带的团队。他们发现,这类环境设计任务与一般强化学习之间具有对称性,并打算加以利用:
一般强化学习:智能体与环境交互,环境是相对固定的,智能体学习一个优化策略,最大化智能体的目标函数;
环境设计任务:智能体与环境交互,智能体是相对固定的,环境学习一个优化其环境参数的策略,最大化环境的目标函数;
那么,真的可以用强化学习的方法设计环境吗?假设答案是肯定的,那么更进一步地,一般强化学习任务中的智能体可以根据不同环境的特点学到不同的优化策略,那么环境设计任务中,我们是否可以猜想环境也能够根据不同智能体的特点,学会不同的优化策略呢?
汪军老师团队就在「Learning to Design Games: Strategic Enviroments in Deep Reinforcement Learning」(学习设计游戏:深度强化学习设计策略性环境)这篇论文中给这两个问题做出了解答。
构建优化目标
论文中根据马尔可夫决策过程(MDP)和智能体的策略函数构建学习范式。
马尔可夫决策过程是强化学习研究中的常用概念, 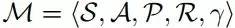
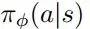
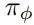
在标准强化学习用法中,马尔可夫决策过程 M 是固定的,只有智能体能够更新自己的策略。为了给模型加上训练环境的能力,论文中首先把状态转换函数 P 参数化为 Pθ,然后给 M 设定一个目标 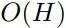
(方程一,这个方程中允许过程 M 和智能体同时达成自己的目标)
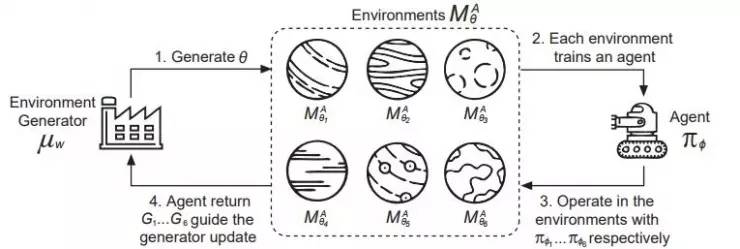
为了进行具体研究,论文中选取了这样一种特定情况进行阐述:环境是对抗性的,环境的目标是让智能体获得的回报最少。从而,要研究的目标函数为:
(方程二,环境的目标为让智能体的回报最少)
优化方法 1 - 转换概率梯度
考虑到许多情况下如上方程二不是解析性的,所以论文中提出了一种转换概率梯度的方法进行优化。
首先假设环境(决策过程)和智能体的参数都是迭代更新的。每一轮迭代中,环境沿梯度方向进行更新,然后智能体根据更新后的环境,更新自己的参数寻找优化策略。
为了找到 θ 的梯度,论文中通过设计一组马尔可夫决策策略对的方式,推导出了一组梯度计算方程,从而可以计算梯度进行这种迭代更新。
图示1:把该方法用于对抗性的迷宫生成的示意图。智能体尝试找到从入口(绿色方块)到出口(红色方块)的最短路径,但是迷宫要让最短路径尽可能地长。沿着 θ 更新的方向,迷宫变得复杂;沿着 φ 更新的方向,智能体找到的路径变得更短。其中回报定义为穿越迷宫所需步数的负数。
优化方法 2:生成式优化范式
在推导梯度方程的过程中,作者们发现这个方程也有不适用的情况:1,受到环境的天然限制,有时Pθ不是可微的,导致基于策略的方法无法使用;2,转换概率模型需要学到一个概率分布,导致基于数值的方法无法使用。
为了解决不适用的问题,作者们提出了一种生成式范式作为梯度方法的替代方法。
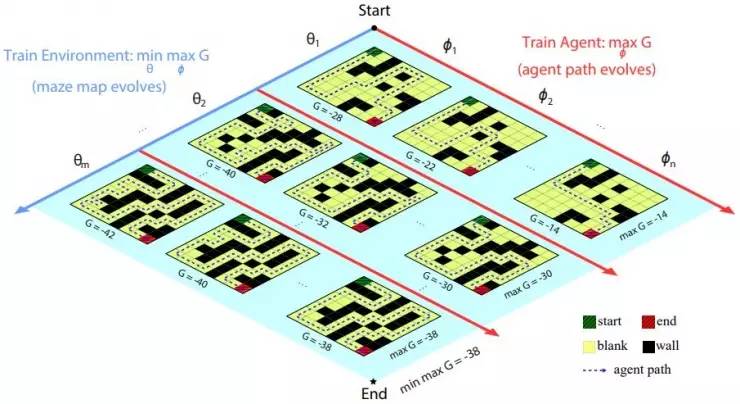
如图,环境生成器首先生成一组参数 θ1~θn,进而形成一组不同的环境。在每一个环境中都单独训练一个智能体获得最优策略,然后在它们各自的环境中观察回报G1~Gn,作为生成器更新下一轮参数的参照。用这样的方法就可以进行环境的迭代更新。
实验验证
论文中用迷宫环境对方法进行了测试,需要智能体以最少的步数从迷宫的左上角走到迷宫的右下角,环境的目标是让智能体能找到的最短路径的步数尽可能多。为了避免生成的墙壁一开始就把智能体堵起来,作者们让环境生成器逐步地增加挡墙,并且放弃会困住智能体的方案。
可微环境
由于正常迷宫的墙壁只有 0 (没有墙壁)或者 1 (有墙壁)两种状态,导致这样的迷宫是不可微的。论文中就设计了一种具有概率性墙壁的迷宫,其中的墙壁能够以一定的概率挡住智能体,这样就成为了一个可微的环境。
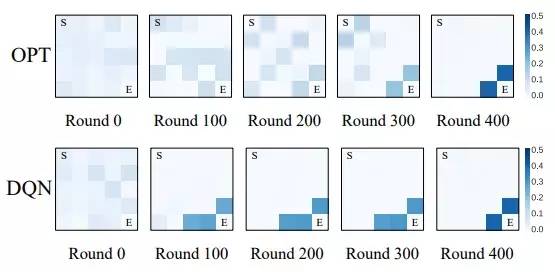
实验中使用了OPT(Optimal,最优)和DQN(Deep Q-network learning)两种智能体,其中OPT智能体是不会学习的,DQN智能体则能够利用深度神经网路把整个地图作为输入,从随机策略开始学习输出向四个方向的动作。
如图中所示,颜色越深的格子表示此处墙壁挡住智能体的可能性越高。可以看到,两个环境都学到了最有效的阻挡位置是在出口附近,同时,由于两个智能体的特性不同(DQN智能体对环境的探索更多),所以与DQN智能体互动的环境更快地找到了近似最优的策略,但是从近似最优收敛到最优却花了很久。
不可微环境
在不可微的正常墙壁测试环境中,论文中还多考虑了一类情况:假设智能体寻找最优路线的能力有限,环境会如何应对?
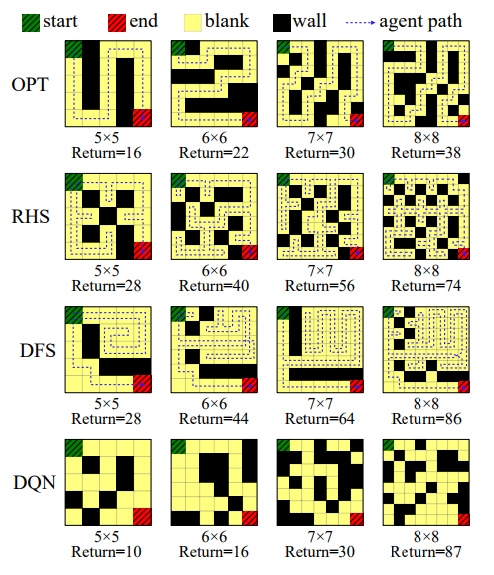
所以除了刚才的OPT和DQN两种智能体外,现在又加入了DFS(深度搜索优先,“撞到南墙再拐弯”)和RHS(右侧搜索优先,保证右侧是墙壁)两种智能体。
如图是环境生成的不同尺寸的迷宫,可以看到,环境为不同的智能体生成的迷宫是不一样的,为OPT(最优路径)智能体生成了狭长无分叉的路径;为RHS(右手优先)智能体生成的迷宫就有很多小的分叉,增大了侧墙的长度;DFS(深度优先)智能体几乎把每个格子都走了两遍;为使用随机策略的DQN智能体生成的迷宫则有一些死胡同。
下面几张动图展示了 8x8 的迷宫在智能体的互动中迭代的、逐渐形成以上特征的过程。
| 迷宫 | 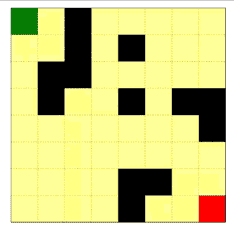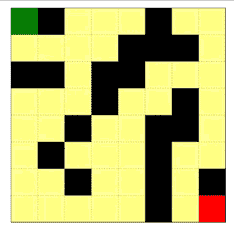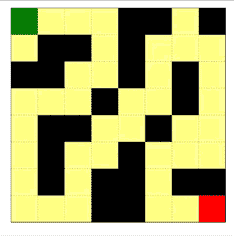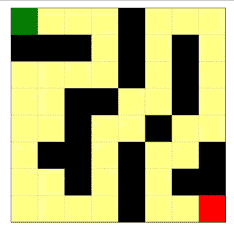 |
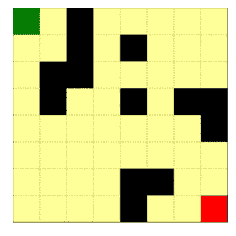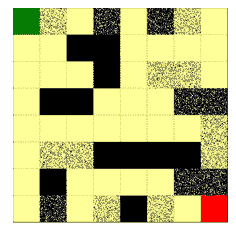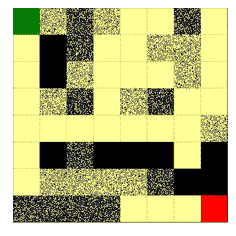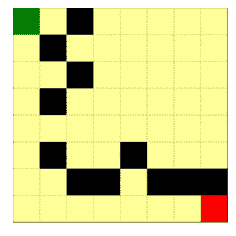 |
 |
 |
| 智能体 | OPT | DFS | RHS | DQN |
这种情况就表明了环境生成器可以根据智能体的弱点,针对性地生成环境。
论文中还有一张学习曲线的分析图,非常清晰地展现了学习过程的对抗性。
对于具有固定策略的OPT、DFS、RHS三种智能体,随着训练进行,生成器可以在一开始就快速学到让步数变多的策略,然后逐渐进行收敛。而DQN智能体则能够随着环境变化不停地更新自己的策略:从学习曲线的不断大幅波动中可以明显看到,有时候智能体的学习速度比环境学习速度快,可以造成所需步数的大幅度下降。
结论
这样,我们在这篇文章开头提的两个问题,“能否让环境强化学习”和“环境能否根据不同智能体的特点学到不同的策略”两个问题就都得到了肯定的答复。论文中也表示会进一步研究如何运用这种方法设计更多环境。
论文原文地址:https://arxiv.org/abs/1707.01310 ,AI 科技评论编译。另外感谢汪军教授帮忙校对此文。