【ICML2022】分支强化学习

分支强化学习

论文链接：

https://www.zhuanzhi.ai/paper/30fefd52a47a458670d26850e1d0f394

强化学习（Reinforcement Learning）是一个经典的在线决策模型。在强化学习中，智能体与未知的环境进行交互，以获得最大的累积奖励。传统强化学习是一个单路径的序列决策模型，智能体在一个状态下只选择一个动作。然而，在推荐系统、在线广告等许多现实应用中，用户们往往会一次选择多个选项，每个选项会触发对应的后继状态，例如，在基于类别的购物推荐中，系统往往会先推荐一些商品的一级类别，当某个一级类别被用户点击时，系统会进一步推荐一些二级类别。在一次购物中，用户可能会选择（触发）多条类别-商品路径，如用户可能会触发“办公设备-打印机-激光打印机”和“办公设备-扫描仪-平板扫描仪”这两条路径。

为了处理这种允许多个动作和多个后继状态的现实场景，微软亚洲研究院的研究员们提出了一种新颖的、树状的强化学习模型，名为分支强化学习（Branching  Reinforcement Learning）。在分支强化学习中，每个状态下，智能体可以选择多个动作，每个状态-动作对有一个潜在的概率被触发。如果一个状态-动作对被成功触发，那么它会根据其潜在的转移分布转移到一个常规的后继状态；如果这个状态-动作对没有被成功触发，那它则会转移到一个“终止状态”（奖励总是为零的吸收态）。由于智能体可能触发多条状态-动作路径，因此它的历史序列决策呈现出一个树状结构。

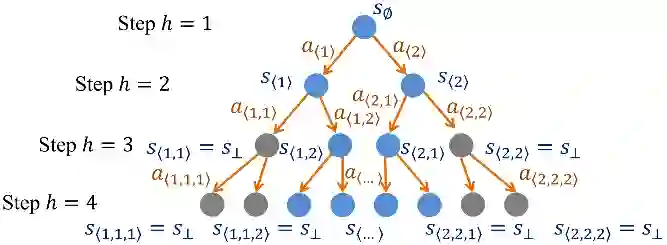
图1：分支强化学习模型示意（当每个状态下允许选择的动作个数为2时）

在分支强化学习这个新的决策模型下，研究员们构建了全新的理论分析工具，包括分支贝尔曼方程（Branching Bellman Equation）、分支价值差异引理（Branching Value Difference Lemma）和分支总方差定律（Branching Law of Total Variance）。研究员们设计了两种计算和采样高效的算法 BranchVI 和 BranchRFE，通过严格的理论分析证明了算法的最优性，并在实验上验证了本文的理论结果。

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“BRL” 就可以获取《【ICML2022】分支强化学习》专知下载链接

                       

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取100000+AI(AI与军事、医药、公安等)主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取100000+AI主题知识资料