【CS224N笔记】一文详解神经网络来龙去脉
 !
!
阅读大概需要25分钟 ![]()
跟随小博主,每天进步一丢丢 ![]()
Neural Networks
The structure of the neural network
A neuron can be a binary logistic regression unit
公式形式:
-
b: We can have an “always on” feature, which gives a class prior, or separate it out, as a bias term------b我们常常认为是偏置
A neural network = running several logistic regressions at the same time
单层神经网络
我们输入一个向量并且通过一系列的逻辑回归函数,我们可以得到一个输出向量,但是我们不需要提前决定,逻辑回归试图预测的向量是什么
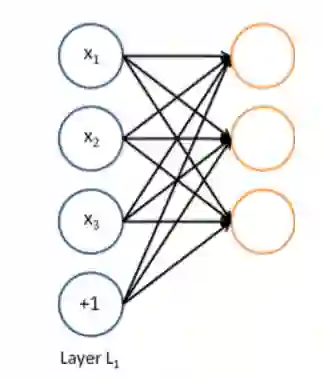
多层神经网络
我们可以通过另外一个logistic回归函数,损失函数将指导中间变量是什么,为了更好的预测下一层的目标。
Matrix notation for a layer--矩阵表示
for example:
我们有:
总结:
f的运算:
非线性的f的必须
-
重要性: -
没有非线性的激活函数,深度神经网络无法做比线性变换更复杂的运算 -
多个线性的神经网络层相当于一个简单的线性变换:$W_1W_2x=Wx$ -
如果采用更多的非线性激活函数,它们可以拟合更复杂的函数
命名主体识别Named Entity Recognition (NER)
-
The task: findand classifynames in text, for example: -
Possible purposes:
-
Tracking mentions of particular entities in documents---跟踪文档中特殊的实体 -
For question answering, answers are usually named entities------回答一些关于命名主体识别的问题 -
A lot of wanted information is really associations between named entities---抽取命名主体之间关系 -
The same techniques can be extended to other slot-filling classifications----可以扩展到分类任务
Why might NER be hard?
-
实体的边界很难计算 -
很难指导某个物体是否是一个实体 -
很难知道未知/新奇实体的类别 -
很难识别实体---当实体是模糊的,并且依赖于上下文
Binary word window classification ---小窗口上下文文本分类器
-
问题: -
in general,很少对单个单词进行分类 -
ambiguity arise in context,一词多义的问题 -
example1:auto-antonyms -
"To sanction" can mean "to permit" or "to punish” -
"To seed" can mean "to place seeds" or "to remove seeds" -
example2:resolving linking of ambiguous named entities -
Paris ->Paris, France vs. Paris Hilton vs. Paris, Texas -
Hathaway ->Berkshire Hathaway vs. Anne Hathaway
Window classification: Softmax
-
Idea: classify a word in its context window of neighboring words---在相邻词的上下文窗口对一个词进行分类 -
A simple way to classify a word in context might be to average the word vectors in a window and to classify the average vector ---一个简单方法是对上下文的所有词向量去平均,但是这个方法会丢失位置信息 -
另一种方法: Train softmaxclassifier to classify a center word by taking concatenation of word vectors surrounding it in a window---将上下文所有单词的词向量串联起来 -
for example: Classify “Paris” in the context of this sentence with window length 2 Resulting vector $x_{window}=x\varepsilon R^{5d}$一个列向量 然后通过softmax分类器
Binary classification with unnormalizedscores ---给分类的结果一个非标准化分数
-
之前的例子中:
-
假设我们需要确认一个中心词是否是一个地点 -
和word2vec类似,我们遍历语料库的所有位置,但是这一次,它只能在一些地方得到高分 -
the positions that have an actual NER Location in their center are “true” positions and get a high score ---它们中符合标准的会获得最高分
Neural Network Feed-forward Computation
采用神经网络激活函数a简单的给出一个非标准化分数
我们采用一个3层的神经网络计算得分
-
s = score("museums in Paris are amazing”)
Main intuition for extra layer
-
中间层的作用学习的是输入词向量的非线性交互----Example: only if “museums”is first vector should it matter that “in”is in the second position
The max-margin loss
-
Idea for training objective: Make true window’s score larger and corrupt window’s score lower (until they’re good enough)---训练思路,让真实窗口的准确率提高,让干扰窗口的得分降低 -
s = score(museums in Paris are amazing) -
最小化 -
这是不可微分,但是是连续的,所以我们可以采用sgd算法进行优化 -
Each window with an NER location at its center should have a score +1 higher than any window without a location at its center -----每个中心有ner位置的窗口得分应该比中心没有位置的窗口高1分
-
For full objective function: Sample several corrupt windows per true one. Sum over all training windows---使用类似于负采样的方法,为真实窗口采样几个错误窗口
矩阵求导---不详细推导
Example Jacobian: Elementwise activation Function
-
多元求导的例子 -
针对我们的公式 进行求导换算:
-
在上面式子中,我们通过链式法则可以得出
note: Neural Networks, Backpropagation
Neural Networks: Foundations
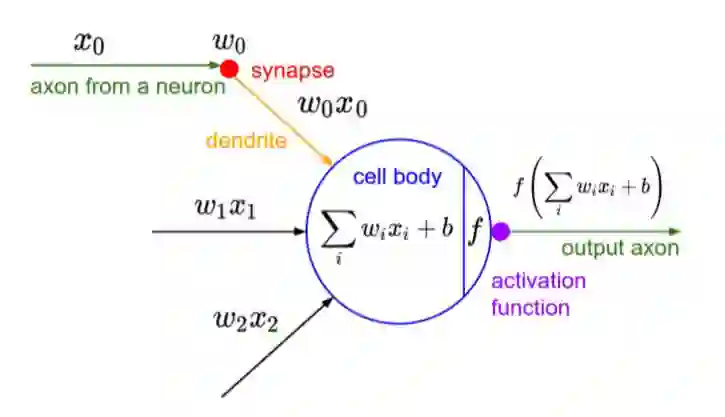
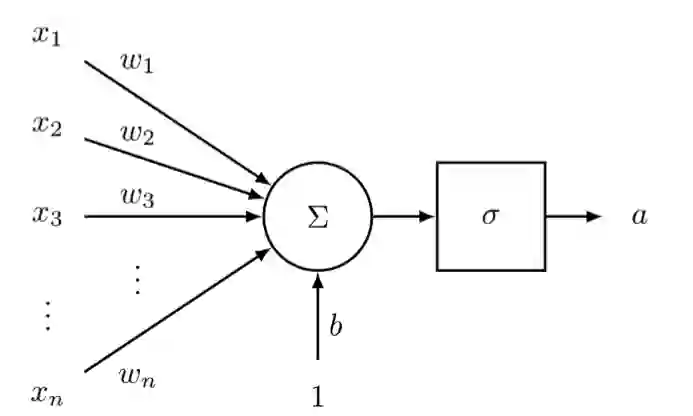
A neuron
-
A neuron is a generic computational unit that takes n inputs and produces a single output. What differentiates the outputs of different neurons is their parameters (also referred to as their weights). -----神经元作用
通过图形可视化上面公式:
我们可以看到,神经元是可以允许非线性在网络中积累的次数之一
A single layer of neurons
-
我们将单个神经元的思想扩展到多个神经元,考虑输入x作为多个这样的神经元输入 -
If we refer to the different neurons’ weights as and the biases as
, we can say the respective activations are
:
-
公式简化
我们可以缩放成: z=Wx+b
激活函数变化为:
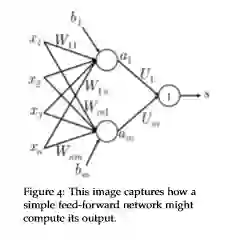
feed-forward computation
-
首先我们考虑一个nlp中命名实体识别问题作为例子: "Museums in Paris are amazing"
我们想判别中心词Paris是不是命名主体。在这种情况下,我们很可能不仅想要捕捉窗口中单词向量,还想要捕捉单词间的一些其他交互,方便我们分类。For instance, maybe it should matter that "Museums" is the first word only if "in" is the second word. --上面可能存在顺序的约束的问题。所以这样的非线性决策通常不能被直接输入softmax,而是需要一个中间层进行score。因此我们使用另一个矩阵 与激活输出计算得到的归一化得分用于分类任务。
这里的f代表的是激活函数
-
Analysis of Dimensions: If we represent each word using a 4 dimensional word vector and we use a 5-word window as input (as in the above example), then the input . If we use 8 sigmoid units in the hidden layer and generate 1 score output from the activations, then
Maximum Margin Objective Function
-
我们采用:Maximum Margin Objective Function(最大间隔目标函数),使得保证对‘真’的数据的可能性比‘假’数据的可能性要高
-
定义符号:Using the previous example, if we call the score computed for the "true" labeled window "Museums in Paris are amazing" as S and the score computed for the "false" labeled window "Not all museums in Paris" as Sc (subscripted as c to signify that the window is "corrupt"). ---正确窗口S,错误窗口Sc
-
随后,我们目标函数最大化S-Sc或者最小化Sc-S.然而,我们修改目标函数来保证误差在Sc>S的时候在进行计算。这么做的目的是我们只在关心‘真’数据的得分高于‘假’数据的得分,其他不是很重要。因此,误差Sc>S时候存在为Sc-S,反之不存在,即为0。所以我们的优化目标是:
-
However, the above optimization objective is risky in the sense that it does not attempt to create a margin of safety. We would want the "true" labeled data point to score higher than the "false" labeled data point by some positive margin ∆. In other words, we would want error to be calculated if (s−sc < ∆) and not just when (s−sc < 0). Thus, we modify the optimization objective: ----上面的优化目标函数是存在风险的,它不能创造一个比较安全的间隔,所以我们希望存在一个这样的间隔,并且这个间隔需要大于0
-
We can scale this margin such that it is ∆ = 1 and let the other parameters in the optimization problem adapt to this without any change in performance.-----有希望了解的可以看svm的推导,这里的意思是说,我们把间隔设置为1,这样我们可以让其他参数在优化过程中自动进行调整,并不会影响模型的表现
梯度更新
-
方向传播是一种利用链式法则来计算模型上任意参数的损失梯度的方法
-
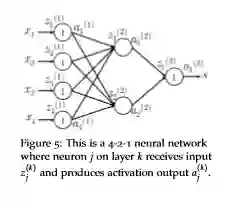
定义:
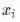 is an input to the neural network. ---输入
is an input to the neural network. ---输入
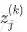 and produces the scalar activation output
and produces the scalar activation output
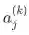 ---每层中的神经元,上角标是层数,下角标的神经元位置
---每层中的神经元,上角标是层数,下角标的神经元位置
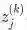 as
as
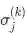 . ---定义z的反向传播误差
. ---定义z的反向传播误差
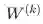 is the transfer matrix that maps the output from the k-th layer to the input to the (k+1)-th -----转移矩阵
is the transfer matrix that maps the output from the k-th layer to the input to the (k+1)-th -----转移矩阵
开始反向传播
-
现在开始反向传播:假设损失函数 为正值, 我们想更新参数
, 我们看到
只参与了
和
的计算。这点对于理解反向传摇是非常重要的一一反向传摇的梯度只受它们所贡献的值的影响。
在随后的前向计算中和
相乘计算得分。我们可以从最大间隔损失看到:
-
我们只分析 其中, 指输入层的输入。我们可以看到梯度计算最后可以简化为
, 其中
本质上是第 2 层中第 i 个神经元反向传播的误差。
与 Wij 相乘的结果, 输入第 2 层中第 i 个神经元中。
Training with Backpropagation – Vectorized
-
对更定的参数 , 我们知道它的误差梯度是
,其中
是将
映射到
的矩 阵。因此我们可以确定整个矩阵
的梯度误差为:
因此我们可以将整个矩阵形式的梯度写为在矩阵中反向传播的误差向量和前向激活输出的外积,并且对于误差的估算: 其中 代表矩阵中每个元素相乘
Neural Networks: Tips and Tricks
Gradient Check
-
Given a model with parameter vector θ and loss function J, the numerical gradient around θi is simply given by centered difference formula:
-
其实就是一个梯度的估计
-
Now, a natural question you might ask is, if this method is so precise, why do we not use it to compute all of our network gradients instead of applying back-propagation? The simple answer, as hinted earlier, is inefficiency – recall that every time we want to compute the gradient with respect to an element, we need to make two forward passes through the network, which will be computationally expensive. Furthermore, many large-scale neural networks can contain millions of parameters, and computing two passes per parameter is clearly not optimal. -----虽然上面的梯度估计公式很有效,但是这仅仅是随机检测我们梯度是否正确的方法。我们最有效的并且最实用(运算效率最高的)算法就是反向传播算法
Regularization ---正则化
-
As with many machine learning models, neural networks are highly prone to overfitting, where a model is able to obtain near perfect performance on the training dataset, but loses the ability to generalize to unseen data. ----和很多机器学习模型一样,神经网络也会陷入过拟合,这回让它无法泛化到测试集上。一个常见的解决过拟合的问题就是采用L2正则化(只需要给损失函数J添加一个正则项),改进的损失函数
-
对上面公式的参数解释,λ是一个超参数,控制正则项的权值大小, 是
第i层的权值矩阵的Froenius范数:Forenius范数=矩阵中每个元素的平方求和在开根号,
-
正则项的作用: what regularization is essentially doing is penalizing weights for being too large while optimizing over the original cost function---在优化损失函数的时候,惩罚数值太大的权值,让权值分配更均匀,防止出现权值过大的情况
-
Due to the quadratic nature of the Frobenius norm (which computes the sum of the squared elements of a matrix), L2 regularization effectively reduces the flexibility of the model and thereby reduces the overfitting phenomenon. Imposing such a constraint can also be interpreted as the prior Bayesian belief that the optimal weights are close to zero – how close depends on the value of λ.-----因为正则化有一个二次项的存在,这有利有弊,它会降低模型的灵活性但是也会降低过拟合的可能性。在贝叶斯学说的认为下,正则项可以优化权值并且使得其接近0,但是这个取决于你的一个λ值的大小
-
Too high a value of λ causes most of the weights to be set too close to 0, and the model does not learn anything meaningful from the training data, often obtaining poor accuracy on training, validation, and testing sets. ---λ取值要合适
为什么偏置没有正则项
-
正则化的目的是为了防止过拟合,但是过拟合的表现形式是模型对于输入的微小变化产生了巨大差异,这主要是因为W的原因,有些w的参数过大。但是b是不背锅的,偏置b对于输入的改变是不敏感的,不管输入改变大还是小。
Dropout---部分参数抛弃运算
-
the idea is simple yet effective – during training, we will randomly “drop” with some probability (1−p) a subset of neurons during each forward/backward pass (or equivalently, we will keep alive each neuron with a probability p). Then, during testing, we will use the full network to compute our predictions. The result is that the network typically learns more meaningful information from the data, is less likely to overfit, and usually obtains higher performance overall on the task at hand. One intuitive reason why this technique should be so effective is that what dropout is doing is essentially doing is training exponentially many smaller networks at once and averaging over their predictions.---------dropout的思想就是在每次前向传播或者反向传播的时候我们按照一定的概率(1-P)冻结神经元,但是剩下概率为p的神经元是激活的,然后在测试阶段,我们使用所有的神经元。使用dropout的网络可以从数据中学到更多的知识
-
However, a key subtlety is that in order for dropout to work effectively, the expected output of a neuron during testing should be approximately the same as it was during training – else the magnitude of the outputs could be radically different, and the behavior of the network is no longer well-defined. Thus, we must typically divide the outputs of each neuron during testing by a certain value --------为了使得的dropout能够有效,测试阶段的神经元的预期输出应该和训练阶段大致相同---否则输出的大小存在很大差异,所以我们通常需要在测试阶段将每个神经元的输出除以P(P是存活神经元的概率)
Parameter Initialization--参数初始化
-
A key step towards achieving superlative performance with a neural network is initializing the parameters in a reasonable way. A good starting strategy is to initialize the weights to small random numbers normally distributed around 0 ---通常我们的权值随机初始化在0附近 是W(fan-in)的输入单元数,
是W(fan-out)的输出单元数
加餐:优化算法----此内容来源于datawhale'颜值担当'
基于历史的动态梯度优化算法结构
SGD
Momentum
NAG
AdaGrad
AdaDelta
Adam
Nadam
下载一:中文版!学习TensorFlow、PyTorch、机器学习、深度学习和数据结构五件套!
![]()
![]()
![]()
后台回复【五件套】
下载二:南大模式识别PPT
![]()
后台回复【南大模式识别】
由于微信平台算法改版,公号内容将不再以时间排序展示,如果大家想第一时间看到我们的推送,强烈建议星标我们和给我们多点点【在看】。星标具体步骤为:
(1)点击页面最上方“深度学习自然语言处理”,进入公众号主页。
(2)点击右上角的小点点,在弹出页面点击“设为星标”,就可以啦。
感谢支持,比心
投稿或交流学习,备注:昵称-学校(公司)-方向,进入DL&NLP交流群。
方向有很多:机器学习、深度学习,python,情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。
记得备注呦
整理不易,还望给个在看!
登录查看更多
相关内容
神经网络(Neural Networks)是世界上三个最古老的神经建模学会的档案期刊:国际神经网络学会(INNS)、欧洲神经网络学会(ENNS)和日本神经网络学会(JNNS)。神经网络提供了一个论坛,以发展和培育一个国际社会的学者和实践者感兴趣的所有方面的神经网络和相关方法的计算智能。神经网络欢迎高质量论文的提交,有助于全面的神经网络研究,从行为和大脑建模,学习算法,通过数学和计算分析,系统的工程和技术应用,大量使用神经网络的概念和技术。这一独特而广泛的范围促进了生物和技术研究之间的思想交流,并有助于促进对生物启发的计算智能感兴趣的跨学科社区的发展。因此,神经网络编委会代表的专家领域包括心理学,神经生物学,计算机科学,工程,数学,物理。该杂志发表文章、信件和评论以及给编辑的信件、社论、时事、软件调查和专利信息。文章发表在五个部分之一:认知科学,神经科学,学习系统,数学和计算分析、工程和应用。
官网地址:http://dblp.uni-trier.de/db/journals/nn/
Arxiv
6+阅读 · 2018年2月20日


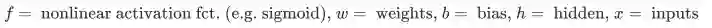

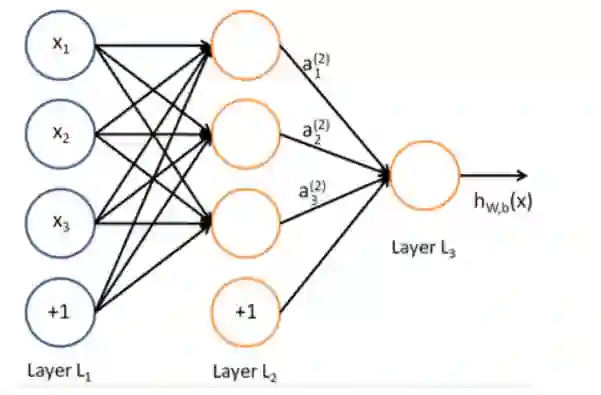
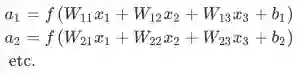
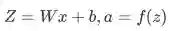




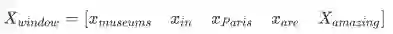
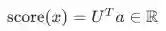
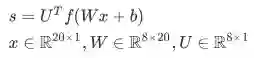

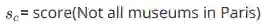
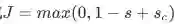
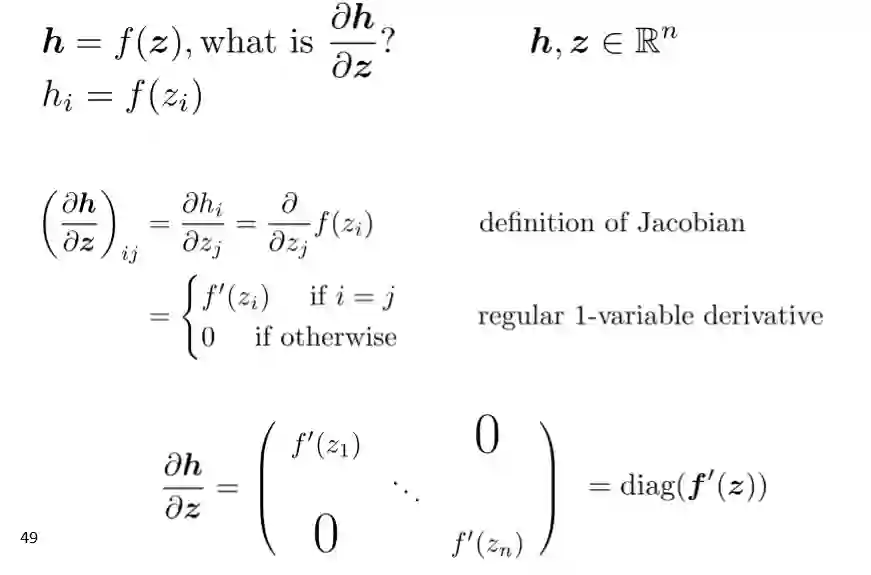
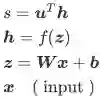


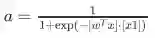
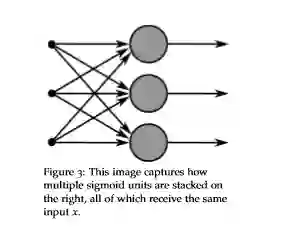
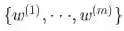 and the biases as
and the biases as , we can say the respective activations are
, we can say the respective activations are 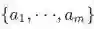 :
:

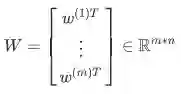

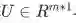 与激活输出计算得到的归一化得分用于分类任务。
与激活输出计算得到的归一化得分用于分类任务。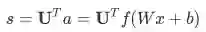
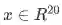 . If we use 8 sigmoid units in the hidden layer and generate 1 score output from the activations, then
. If we use 8 sigmoid units in the hidden layer and generate 1 score output from the activations, then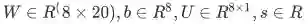

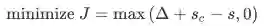
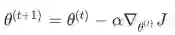
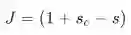 为正值, 我们想更新参数
为正值, 我们想更新参数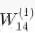 , 我们看到
, 我们看到  和
和 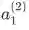 的计算。这点对于理解反向传摇是非常重要的一一反向传摇的梯度只受它们所贡献的值的影响。
的计算。这点对于理解反向传摇是非常重要的一一反向传摇的梯度只受它们所贡献的值的影响。 相乘计算得分。我们可以从最大间隔损失看到:
相乘计算得分。我们可以从最大间隔损失看到: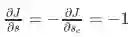
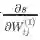
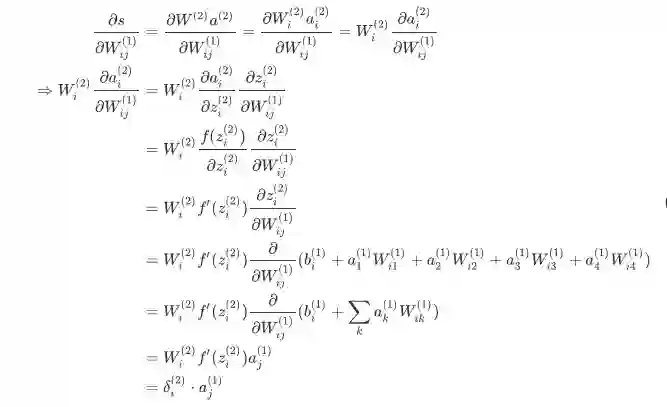
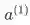 指输入层的输入。我们可以看到梯度计算最后可以简化为
指输入层的输入。我们可以看到梯度计算最后可以简化为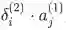 , 其中
, 其中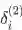 本质上是第 2 层中第 i 个神经元反向传播的误差。
本质上是第 2 层中第 i 个神经元反向传播的误差。 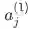 与 Wij 相乘的结果, 输入第 2 层中第 i 个神经元中。
与 Wij 相乘的结果, 输入第 2 层中第 i 个神经元中。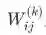 , 我们知道它的误差梯度是
, 我们知道它的误差梯度是 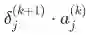 ,其中
,其中 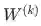 是将
是将 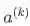 映射到
映射到 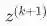 的矩 阵。因此我们可以确定整个矩阵
的矩 阵。因此我们可以确定整个矩阵 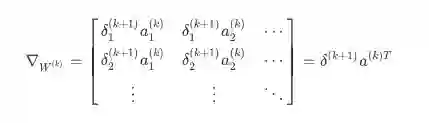
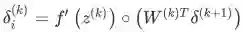
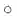 代表矩阵中每个元素相乘
代表矩阵中每个元素相乘
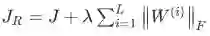
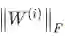 是
是 第i层的权值矩阵的Froenius范数:Forenius范数=矩阵中每个元素的平方求和在开根号,
第i层的权值矩阵的Froenius范数:Forenius范数=矩阵中每个元素的平方求和在开根号,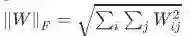

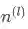 是W(fan-in)的输入单元数,
是W(fan-in)的输入单元数,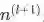 是W(fan-out)的输出单元数
是W(fan-out)的输出单元数

















