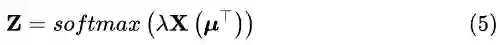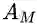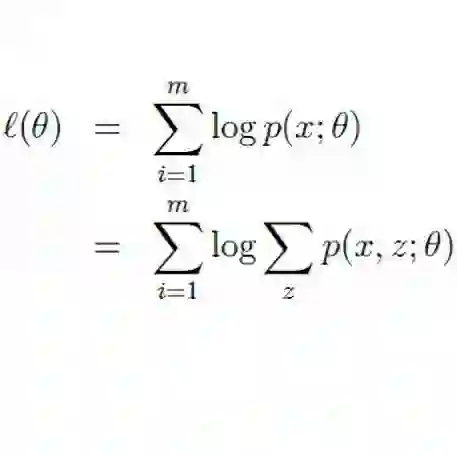ICCV 2019 Oral | 期望最大化注意力网络 EMANet 详解
作者 | 立夏之光
编辑 | 唐里
背景介绍
期望最大化注意力机制
前提知识
期望最大化算法
期望最大化(EM)算法旨在为隐变量模型寻找最大似然解。对于观测数据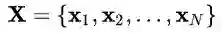
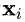
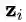

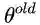
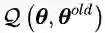
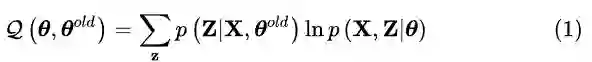
M步通过最大化似然函数来更新参数得到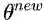
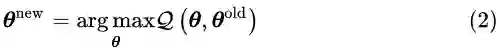
EM算法被证明会收敛到局部最大值处,且迭代过程完整数据似然值单调递增。
高斯混合模型(GMM)是EM算法的一个范例,它把数据用多个高斯分布拟合。其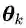
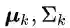
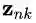
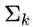
非局部网络
非局部网络(Nonlocal)率先将自注意力机制使用在计算机视觉任务中。其核心算子是:
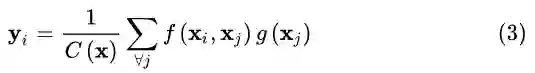
其中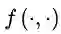
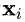
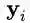
期望最大化注意力机制
期望最大化注意力机制由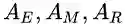
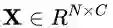
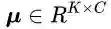
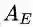
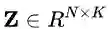
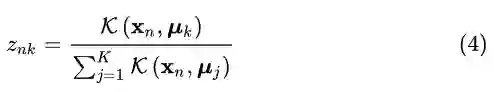
在这里,内核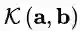
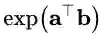
其中,λ作为超参数来控制Z的分布。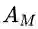
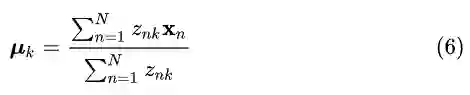
值得注意的是,如果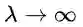
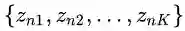
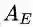
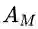
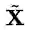

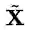
综上,EMA在获得低秩重构特性的同时,将复杂度从Nonlocal的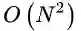
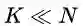
期望最大化注意力模块
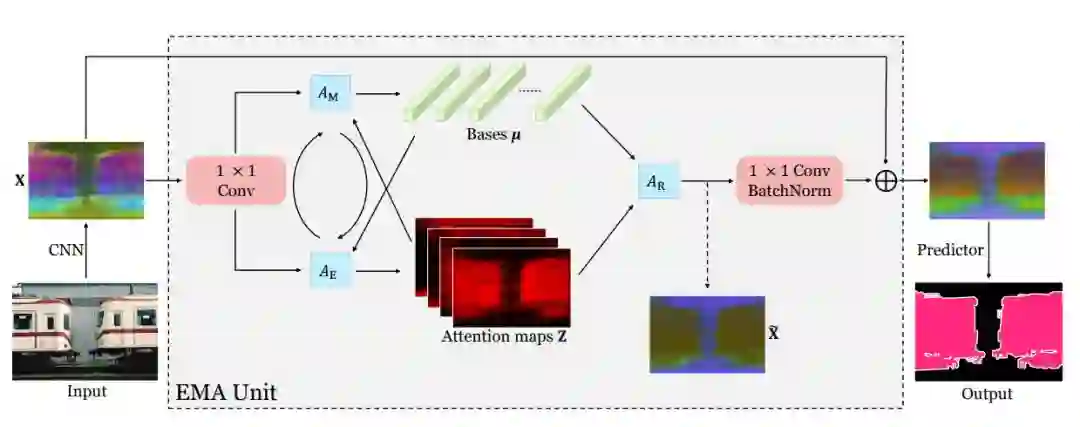
EMA Unit
期望最大化注意力模块(EMAU)的结构如上图所示。除了核心的EMA之外,两个1*1卷积分别放置于EMA前后。前者将输入的值域从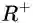


对于EM算法而言,参数的初始化会影响到最终收敛时的效果。上一节中讨论了EMA如何在单张图像的特征图上进行迭代运算。而对于深度网络训练过程中的大量图片,在逐个批次训练的同时,EM参数的迭代初值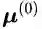
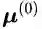
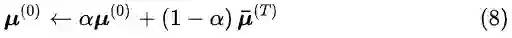
其中,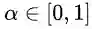
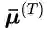
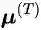
此外,EMA的迭代过程可以展开为一个RNN,其反向传播也会面临梯度爆炸或消失等问题。此外,公式(8)也要求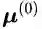
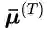
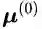
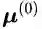
此处,我们可以考虑下EMA和A2Net[5]的关联。A2Net的核心算子如下:
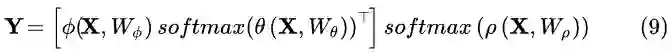
其中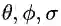
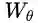
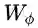
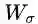
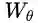
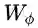
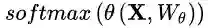
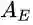
迭代一次。因此,A2-Block可以看作EMAU的特殊例子,它只迭代一次EM,且μ由反向传播来更新。而EMAU迭代T步,用滑动平均来更新μ。
实验
首先是在PASCOL VOC上的消融实验。这里对比了不同的μ更新方法和归一化方法的影响。
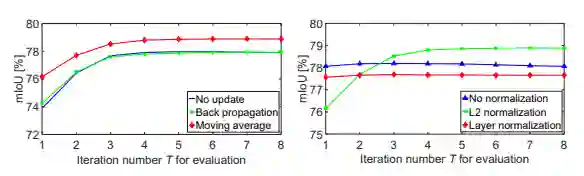
可以清楚地看到,EMA使用滑动均值(Moving average)和L2Norm最为有效。作为对比,Nonlocal和A2Net的模块作为语义分割头,在同样设置下分别达到 77.78%和77.34%的分数,而EMANet仅迭代一次时分数为77.34%,三者无显著差异,符合上文对Nonlocal和A2Net的分析和对比。接下来是不同训练和测试中迭代次数Τ的对比实验。
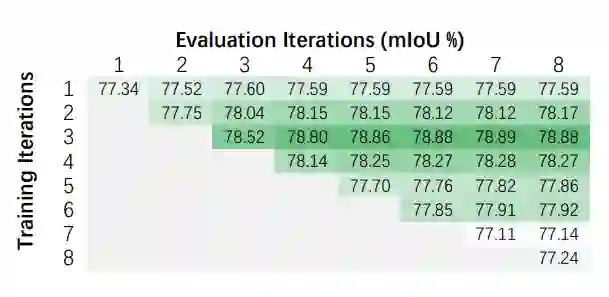
可以发现,EMA仅需三步即可近似收敛(精度不再增益)。而随着训练时迭代次数的继续增长,精度有所下降,这是由EMA的RNN特性引起的。
接下来,是EMANet和DeeplabV3、DeeplabV3+和PSANet的详细对比。
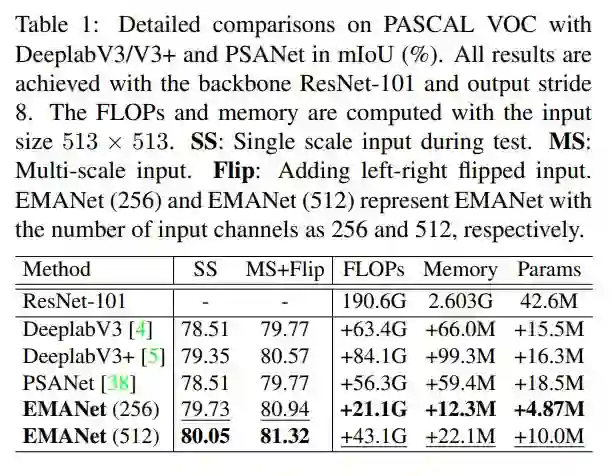
可以发现,EMANet无论在精度还是在计算代价上,都显著高于表中几个经典算法。
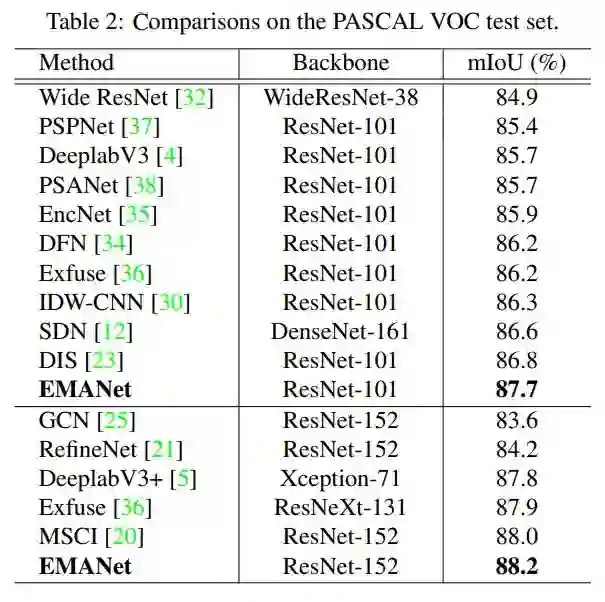
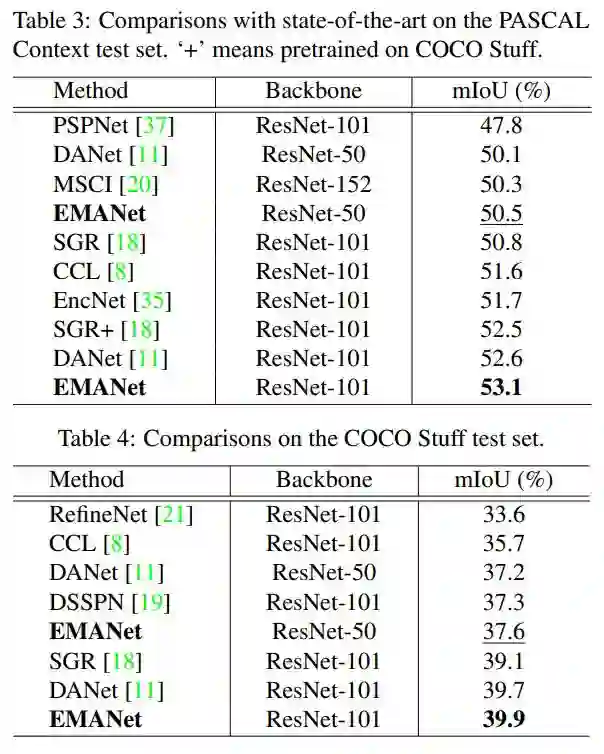
在VOC test server上,EMANet在所有使用ResNet-101的算法中,取得了最高的分数。此外,在PASCAL Context和COCO stuff数据集上也表现卓越。
最后是学习到的注意力图的可视化。如下图,i,j,k,l表示四个随机选择的基的下标。右边四列绘出的是它们各自对应的注意力图。可以看到,不同的基会收敛到一些特定的语义概念。

参考资料:
[1] FCN https://people.eecs.berkeley.edu/~jonlong/long_shelhamer_fcn.pdf
[2] Deeplab https://arxiv.org/abs/1606.00915
[3] PSPNet https://arxiv.org/abs/1612.01105
[4] Non-local Neural Networks https://arxiv.org/abs/1711.07971
[5] A2Net https://papers.nips.cc/paper/7318-a2-nets-double-attention-networks.pdf

张钹院士:人工智能的魅力就是它永远在路上 | CCAI 2019
Facebook 自然语言处理新突破:新模型能力赶超人类 & 超难 NLP 新基准
巴赫涂鸦创作者 Anna Huang 现身上海,倾情讲解「音乐生成」两大算法

点击“阅读原文”查看 用于场景分割的双注意力网络