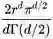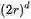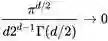陈陟原：数据降维与可视化| AI 研习社第 53 期猿桌会

2018 年 9 月 2 日 AI科技评论

相信大多数人都已经接触过数据可视化——Excel 随便画一张表就是了。众所周知，二维数据可视化很容易，条形图、饼状图等等，我们在初中就已经学过了。那么三维数据呢？可能有些接触到音频产品的朋友会说瀑布图，很好。而 N 维数据呢？物理学告诉我们：低维空间只能观察到高维空间在本维度的投影。既然我们本身的维度无法增加，那么就只能想办法把数据的维度降低了。

近日，在雷锋网 AI 研习社公开课上，澳大利亚国立大学信息技术专业学生陈陟原就分享了数据降维与可视化的相关内容。公开课回放视频网址：http://www.mooc.ai/open/course/526

陈陟原：澳大利亚国立大学信息技术专业学生。现在在北京大学做国际暑期教学助理。曾加入雷锋字幕组翻译过 CS231n 斯坦福李飞飞计算机视觉课程和 CS224n 自然语言处理。

分享主题：数据降维与可视化

分享大纲：

• 高维数据实例&高纬度空间模型

• 维数灾难&降维为什么如此重要

• 常用的线性和非线性降维方法

AI 研习社将其分享内容整理如下：

我是陈陟原，澳大利亚国立大学信息技术专业，目前方向是高性能计算。今天要跟大家分享的是流行学习：数据降维与可视化。

我前段时间去了一次上海，见了一下之前关系很好的学长以及一些澳国立的校友。

在和他们吃饭的时候我们讨论了很多工作方面的问题。其中有一个在银行工作的学长就跟我说起现在 BI 如何如何啊，数据可视化怎样怎样啊。

这也是为什么今天我想跟大家聊聊数据可视化。今天的讲座不会很深，我只是跟大家浅显的介绍一下。有什么问题也欢迎大家课后与我联系，也可以在网上找一些更深入的资料。

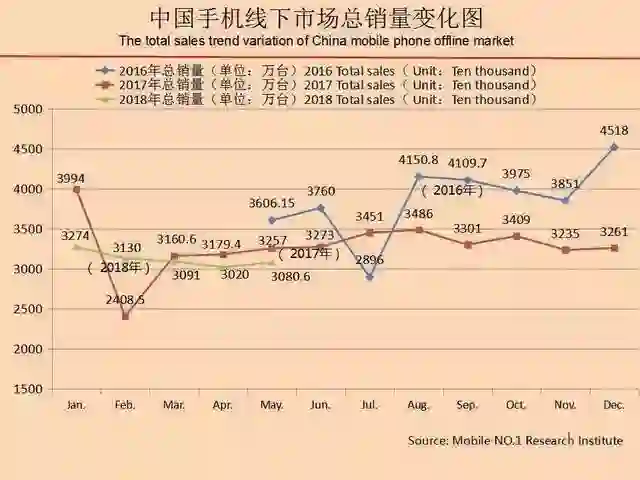
我在这里用了网上找的一张图，题目是大家可能都会比较感兴趣的——智能手机出货量。

在这张图当中，横轴是月份（时间），纵轴就是出货量。它是一个十分完美的数据可视化例子，这样的图相信大家两分钟能做一堆。

所以，我想也没什么要跟大家分享得了，本次讲座到此圆满结束，感谢大家的参与。希望大家能继续支持雷锋，继续支持 AI 研习社。

--当然，这是不可能的。

子曰：「一个好的讲座，应该从视频开始」。虽然说现在讲座已经开始 2 分钟了，但也不算太晚。

这个视频其实有五年的历史了，是当时 IBM 为了宣传智慧星球制作的，可见他们这种全民机器学习开始的时间有多早。我很希望大家都听懂了这个视频，因为我也没有找到字幕。

该视频主要介绍了 IBM 的机器学习如何提高这家面包店的销量——重点是，数据。

对于面包店来说，影响销量的因素有很多。比如说，外面的温度、湿度、降雨量——仅仅是天气就已经不止三个维度了，还有堵车情况（出门晚了来不及吃早饭），甚至世界杯的成绩都会对它产生影响。所以，我们要画一张怎么样的图来把这么多维度的东西都扔进去呢？

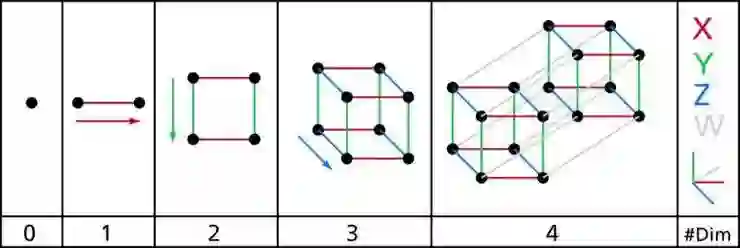
上面这张图最左边是零维，点。后面依次为：一维，线；二维，面；三维，体。而最后的这个四维，叫正方……正方什么来着？反正，它叫什么不重要，重要的是它是四维的。我不知道有没有人看过《三体》，它最后一本书中对四维有一些描述。这是个不存在于三维空间的角度，既然不存在，我们也不可能看得到而只能去想象。

大家记住这点就够了，有人让你做个面包店销量的可视化，你就甩他一脸这种图，说：你自个儿去想象吧。

说正经的，就为了画张表就搞一堆机器学习算法？北京六院要不要了解一下？

这里虽然我已经假设大家都有机器学习背景，但考虑到现在全民机器学习，这里应该也还有非计算机、数学专业的听众，他们没有足够的基础，所以我还是要简单介绍一下维数灾难，想要更深入地学习的同学，也可以进一步在网上搜寻相关资料。

我们知道维数越高精确度越高，比如天气预报会包括温度、湿度以及风向、风力、降雨量……至少经验告诉我们，这样的天气预报精度是会更高的。那么是不是可以进行延展，认为对于所有情况来说，维数都越高越好呢？

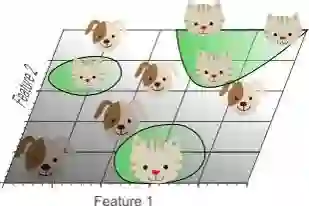
首先我们看一下图，图上是一堆汪和喵，我们该怎么把它们分类出来呢？看上去不太好分类。

那我们稍稍做一下扩展，多加一个维度，图就有了两个特征，即两个维度。

虽然这样看起来分类效果也算不错了，但还可以更好吗？

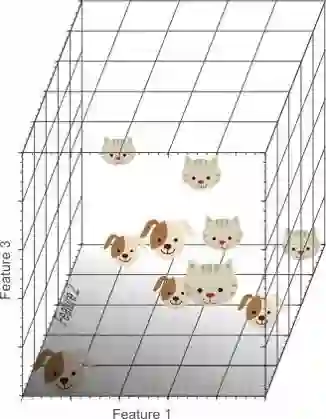
那么再多加一个特征呢？

嗯，完美。虽然可能看上去有些不是很直观哈。听我口令，变

嗯，非常不错，完美的将喵和汪们分开了。

看到上面这张图，Hmmmm 这似乎有些不对啊。嗯你没猜错，过拟合了。我相信大家都知道什么是过拟合，也都清楚为什么我们那么讨厌过拟合，这里不再赘述。

而除此之外，我们还有一个更加令人难受的东西，如果你学过 kNN 的话那你肯定知道——维度灾难。

很多算法都基于一个重要的基本假设：任意样本附近任意小的距离内总能找到一个训练样本，即训练样本的采样密度足够大，也称为「密采样」，才能保证分类性。

我们知道，维度增长是指数级的。10x10 的正方形用一百个样本就能填满，10x10x10x10 的四维体就需要一万个。2009 年的 KDD Challenge 就找了 15000 个维度，你有再大的样本量也是十分稀疏的。

除了上面两点之外，还有一点极其重要，那么就是距离。我们知道，在高维空间下不同样本对之间的距离的差别与我们熟知的三维空间有很大的不同。这里我们做一个简单的证明：

在一个 d 维空间当中，超球体的体积是这样的：

，超正方体的体积则是这样的：

。当我们有无穷多个维度时，也即 d 趋近于无穷时，超球体与超正方体的体积比会很不幸：

这个故事告诉我们，高维空间当中几乎所有数据都会远离中心，两个关联很强的数据对之间的距离可能比你想象当中要大很多，在此情况之下，距离函数失去了意义。

所以，我们的目标是—降低维度。

该怎么降低维度呢？

相信看过《三体》的人都清楚：流形学习。在继续进行到数据降维的操作之前，这里我先简单介绍一下流行。

这张图上，有一个碗、一个杯子和一个甜甜圈。

我们首先引入一个「同胚」的概念。什么样的东西是同胚的呢？

通过连续变换（拉伸、弯曲、撕裂或者粘合）之后能变成一样的两个或多个物体，这些物体就是同胚的。在这个例子当中，杯子和甜甜圈中间都有一个圈，所以它们是同胚的。

然后我们再引入一个「亏格」的概念，以实的闭曲面为例，亏格 g 就是曲面上洞眼的个数，亏格数相同的物体就是同胚的。在这个例子中，碗的亏格为 0，而杯子和甜甜圈的亏格都为 1，所以杯子和甜甜圈是同胚的。

这里我们为什么提到流形呢？它是指我们可以假设这些东西都是随意变化的。比如说，要把玻璃、塑料碗揉成一个杯子的形状，也是有困难的。

所以说这跟降维有什么关系？我们再来看一张图。

这个是地球。而我们都知道一个欧式空间当中的球体，是三维的。

这个则是地图，就是把球体铺平后的样子。

所以说，球面是几维的呢？看这个图就知道——二维。原本表达我们的位置需要三个变量，这么一来就只需要两个了，即我们成功将维度降低为两个。

所谓流形学习，就是假设在欧式空间当中存在这样一个流形，它可以把维度降低下来。这里再提一下，一个 d 维的流形，即任意点处局部同胚于欧氏空间，对于地球上的任意一点，我们在地面看到的都是平的，我们就可以认为它局部同胚于欧式空间，这是一个二维的东西。

接下来，我们正式讨论流行学习算法。

首先是线性流行学习算法。这里我们一共会讨论两种算法：无监督的 PCA，与监督的 LDA。

第一种算法是 PCA，即主成分学习（Principal Component Analysis），它借助于一个正交变换，将其分量相关的原随机向量转化成其分量不相关的新随机向量，这在代数上表现为将原随机向量的协方差阵变换成对角形阵，在几何上表现为将原坐标系变换成新的正交坐标系，使之指向样本点散布最开的 p 个正交方向，然后对多维变量系统进行降维处理，使之能以一个较高的精度转换成低维变量系统，再通过构造适当的价值函数，进一步把低维系统转化成一维系统。

简单来说，就是通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。PCA 则是指找出数据里最主要的方面，用数据里最主要的方面来代替原始数据。而 PCA 算法则主要从线性的协方差角度去找较好的投影方式。

另外一个常用的算法是 LDA，即线性判别分析（Linear Discriminant Analysis）。和 PCA 不同，LDA 是根据类别的标注关注分类能力。所以说 LDA 降维是直接和类别的个数 k 相关的，也不保证投影到的坐标系是正交的。

假设我们的原始数据是 d 维的，一共有 k 个类别。PCA 可以选择的维度范围是 1--d，而 LDA 跟维度关系不大，监督学习主要关注标签，它可选择降到的维度范围是 1--k-1（类别数-1）。这给 LDA 造成了使用方面的限制，比如说类别为 3，那就无法让它降到 3 维，类比为 10，最多是能让它降到 9 维。但是在大多数情况下，LDA 的降维效率要比 PCA 稍微高一些。

刚刚讲到维数灾难的时候，第三点（距离问题）没有仔细提。

在降维的时候，我们通常通过投影方式降维，然而很多数据在获取低维度的投影过程中，会丢失很多数据，尤其是距离信息，即原始距离的数据，在降维以后会产生新的变化。比如欧氏空间的原本距离为 10，降维之后，就变成 8 了，而在另一个维数中的数据还可能变成 2 了，这就会导致降维后的结果不够收敛，因而分类效果也降低——这是由于线性降维的线性原理所导致的。

因此我们就只能通过非线性流形学习来解决这个问题。关于非线性流形学习，我只会简要介绍 T-SNE（t-distributed Stochastic Neighbor Embedding）算法。

T-SNE 算法将数据点之间的相似度转换为概率，它通过原始空间和嵌入空间的联合概率的 Kullback-Leibler（KL）散度来评估可视化效果的好坏，也就是说用有关 KL 散度的函数作为 loss 函数，然后通过梯度下降最小化 loss 函数，最终获得收敛结果。

简单来说，就是原始空间中的相似度由高斯联合概率表示，嵌入空间的相似度由「学生 t 分布」表示。至于为什么我们愿意使用 T-SNE？就是因为它的表现效果特别好——它主要关注数据的局部结构，同时，这也会导致它的时间和空间复杂度都非常高。

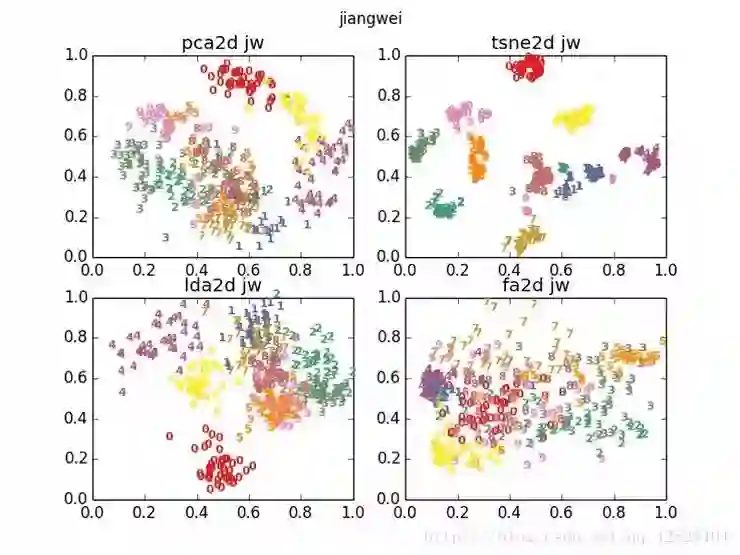
接下来，我们对线性降维和非线性降维做一个简要的对比。