稠密vs.稀疏编码，哪个更好用？

2017 年 11 月 19 日 KingsGarden Mr. King

目录

什么是稀疏编码？
矢量量化（Vector Quantization--VQ）
非负矩阵分解（Non-negative Matrix Factorization--NMF）
其他稀疏模型
稀疏化方法

前言：来一回标题党:-) 编码，通俗的讲，就是对我们所观测到的进行整理和归纳的结果。例如，大部分的苹果从外观上可以编码为具有红色、圆形、光滑的一种果实（颜色、形状、质感等特点）。编码的目的是用于特征化以及区分我们的观测。为了更好的实现这一目标，人类通常会采用不同的编码，例如，对于植物学家而言，苹果的编码是“蔷薇科，苹果属，落叶乔木”；对于营养学家而言，苹果的编码又是“性平，味甘，含丰富矿物质和维生素，低脂”。同样地，稀疏编码和稠密（通常情况下的编码都是稠密的）编码，也是应运着我们不同的需求而生，没有绝对的好坏之分，而我们这期的重点更多的是来讲讲关于”稀疏编码“的故事。

1 什么是稀疏编码？

稀疏编码从字面上可以理解为具有稀疏结构的一种编码方式。相比于一般的编码结构，稀疏编码通常只需要使用到编码中的少数几个维度即能刻画对应的事物（见图1）。直观上讲，这种编码方式便于存储和访问，因此也便于检索。有一种游戏，不少人都玩过，有一人心中默想一样事物，周围的人通过不断的提问，去猜出刚才他心里想的。例如，“能吃么？”—是（答）；“是水果么？”—是；“一般是红色的么？”—是；“要削皮么？”—是；“北方的产地主要在山东么？”—是。相信此刻“苹果”这个答案大家一定猜的八九不离十了吧。和玩这种游戏一样，不仅要猜出出迷人心里所想的，更要用采用最少的回合数（问题）来完成。采用稀疏编码和玩这种游戏有类似的地方，需要利用最少的有效编码位，准确地区分和刻画事物。那么，如何来获得稀疏编码呢？

图 1 普通编码和稀疏编码

2 矢量量化（VectorQuantization--VQ）

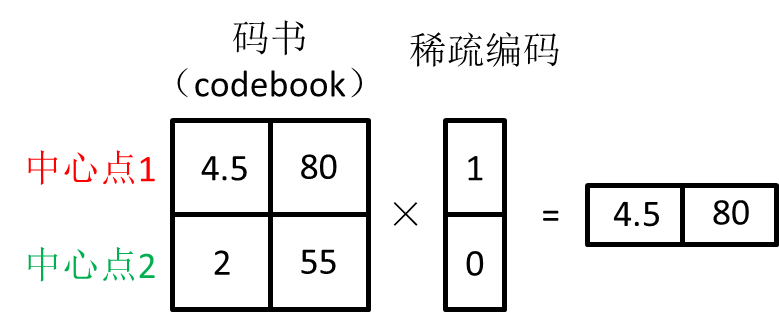
矢量量化是一种数据压缩技术，目前主要在语音、图像和视频的压缩中被广泛使用。矢量量化的核心思想很简单，将相似数据进行聚类，同一类中的数据点用一个代表值来替换，并将所有的数据用一个矢量表示。举一个简单的例子，如图2所示，数据分布在一个二维平面中，根据矢量量化的原理，1）先将数据进行聚类；2）找到数据聚类的中心点：(4.5, 80)和(2, 55)，并生成码书（code book）；3）将所有数据按照码书，生成对应的稀疏编码。这种编码的优点是能够对原始数据产生非常高的数据压缩比（在图2的例子中，所有二维平面上的数据只用了2个数据点即可表示），且简单易行。我们所熟悉的jpeg，mpeg-4等媒体的压缩格式中，都有利用矢量量化进行数据编码的过程。在矢量量化中，稀疏编码表示的是数据所属的分类信息。矢量量化的技术难点在于定义码书的过程，从最早通过解多维积分问题到后来通过数据训练（LBG-VQ，SDL，K-SVD）获得，其技术已逐步成熟并市场化。

（a）

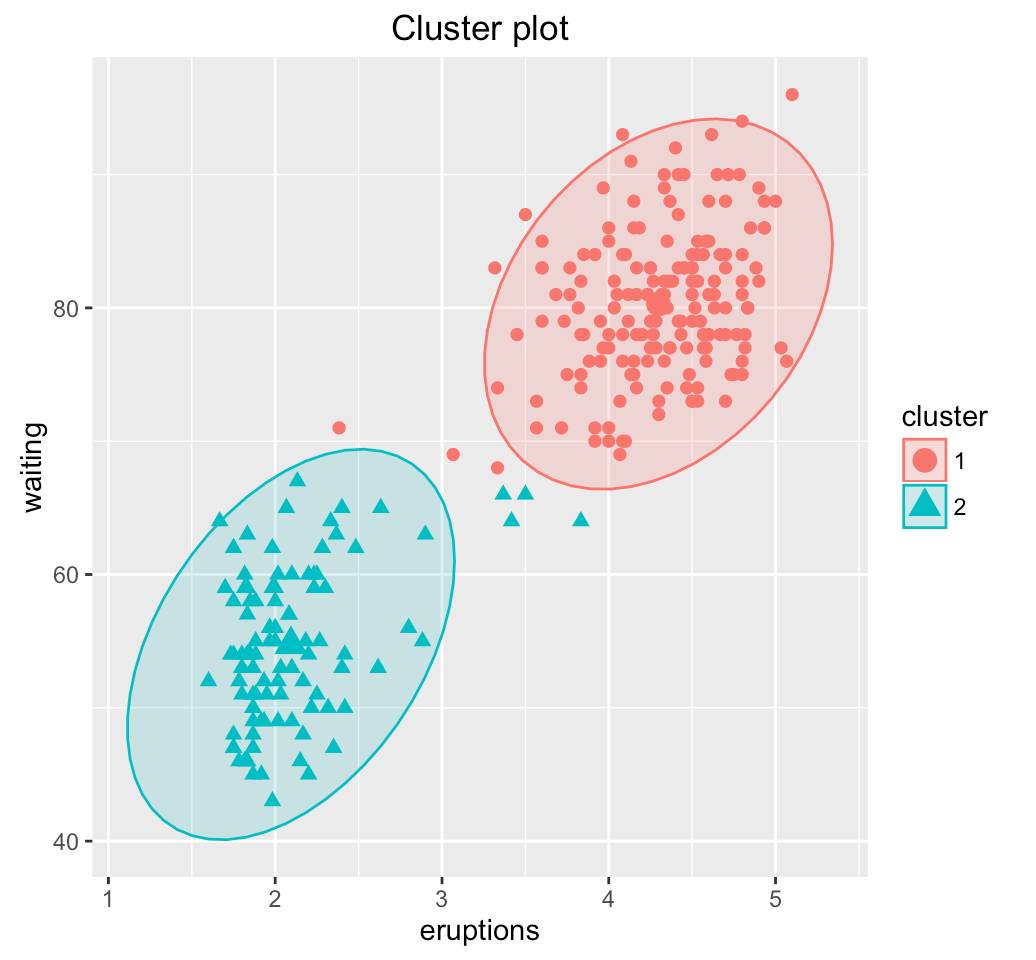
（b）

图 2 矢量量化示例。（a）原始数据分布；（b）对原始数据的矢量量化

3 非负矩阵分解（Non-negativeMatrix Factorization--NMF）

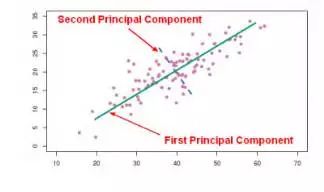
非负矩阵分解是矩阵分解的一类方法。先来简要介绍下矩阵分解。和矢量量化相同的是，矩阵分解可以被用来作为数据压缩的一种手段。不同的是，矩阵分解是通过保持原有信息尽可能不丢失的基础上，找到用于数据压缩的一组基。用一种比较形象的方式解释：原有数据（例如，人的行为数据、交通数据、气象数据等等）坐落在一个高维的空间（n维空间）中，矩阵分解的目的是把原有的数据 “塞”到一个新的（k维，n远远大于k）空间中，同时还希望尽可能的保证原有数据信息不丢失。如图3所示，我们可以利用矩阵分解，找到二维数据空间的一维表示（绿色直线—压缩后的基向量，这里保证数据的散度尽可能不丢失），从而起到数据压缩的作用。

图 3 矩阵分解示例：将二维的数据点投影到绿色的直线（一维空间）上

矩阵分解的方法有很多，像PCA，SVD，MF，PMF都是经典的矩阵分解方法。对比这些经典的方法，以及今天我们要说的主题，非负矩阵分解的优点是什么，又为什么能够获得稀疏编码呢？

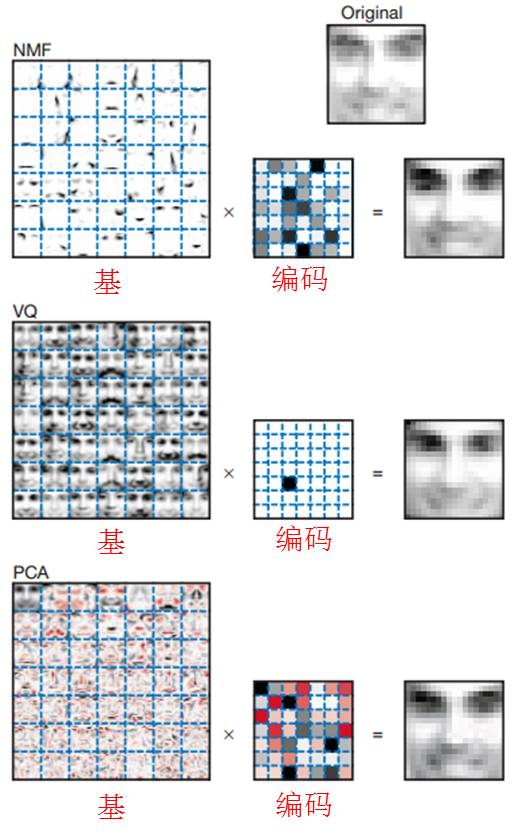
所有的优点和获得稀疏编码的原因归结起来只有一点，非负矩阵分解中采用了对结果的“非负”约束。结合图 4关于人脸表示的示例想象一下，在非负矩阵分解的过程中，所有结果只有一个方向（非负约束），因此所得到的基对原数据也只有一类表示—这通常是原始数据的局部刻画。而原始数据通常是这些局部表示的一种组合，因此所得的编码也是稀疏的。图 4还给出了关于PCA，VQ和NMF的形象比较，可以看到，通过PCA所得到的基，基本没有产生可解释的图像表示，且编码也是稠密的。通过VQ所得的每一个基，都是对原始图像的一种全局描述，因此其编码也最为稀疏。而通过NMF所得的基能够表示人脸的一部分，通过对部分的组合，获得对原始数据的压缩表示。