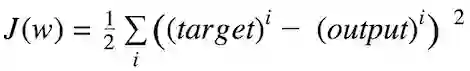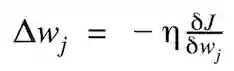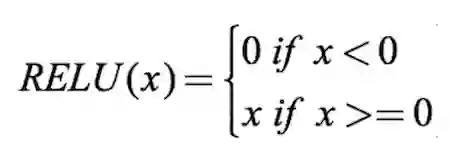基于Python入门深度学习

来源：Medium

编译：weakish

编者按：Python软件基金会成员（Contibuting Member）Vihar Kurama简明扼要地介绍了深度学习的基本概念，同时提供了一个基于Keras搭建的深度学习网络示例。

深度学习背后的主要想法是，人工智能应该借鉴人脑。这一观点带来了“神经网络”这一术语的兴起。大脑包含数十亿神经元，这些神经元之间有数万连接。深度学习算法在很多情况下复现了大脑，大脑和深度学习模型都牵涉大量计算单元（神经元），这些神经元自身并不如何智能，但当它们互相交互时，变得智能起来。

我觉得人们需要了解深度学习在幕后让很多事情变得更好。Google搜索和图像搜索已经使用了深度学习技术；它允许你使用“拥抱”之类的词搜索图像。

—— Geoffrey Hinton

神经元

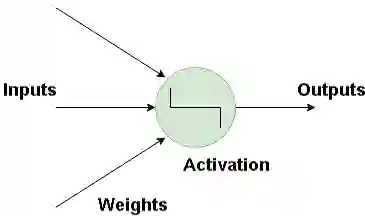
神经网络的基本构件是人工神经元，人工神经元模拟人脑神经元。它们是简单而强大的计算单元，基于加权的输入信号，使用激活函数产出输出信号。神经元遍布神经网络的各层。

人工神经网络如何工作？

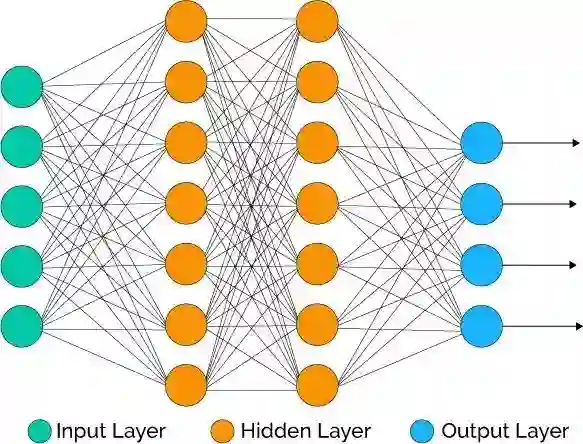
深度学习包含建模人脑中的神经网络的人工神经网络。当数据流经这一人工网络时，每层处理数据的一个方面，过滤离散值，识别类似实体，并产生最终输出。

输入层（Input Layer） 这一层包含的神经元仅仅接受输入并将其传给其他层。输入层中的神经元数目应当等于数据集的属性数或特征数。

输出层（Output Layer） 输出层输出预测的特征，基本上，它取决于构建的具体模型类别。

隐藏层（Hidden Layer） 在输入层和输出层之间的是隐藏层。在训练网络的过程中，隐藏层的权重得到更新，以提升其预测能力。

神经元权重

权重指两个神经元之间的连接的强度，如果你熟悉线性回归，你可以将输入的权重想象成回归公式中的系数。权重通常使用较小的随机值初始化，例如0到1之间的值。

前馈深度网络

前馈监督神经网络是最早也是最成功的神经网络模型之一。它们有时也称为多层感知器（Multi-Layer Perceptron，MLP），或者简单地直接称为神经网络。

输入沿着激活神经元流经整个网络直至生成输出值。这称为网络的前向传播（forward pass）。

激活函数

激活函数将输入的加权和映射至神经元的输出。之所以被称为激活函数，是因为它控制激活哪些神经元，以及输出信号的强度。

有许多激活函数，其中最常用的是ReLU、tanh、SoftPlus。

图片来源：ml-cheatsheet

反向传播

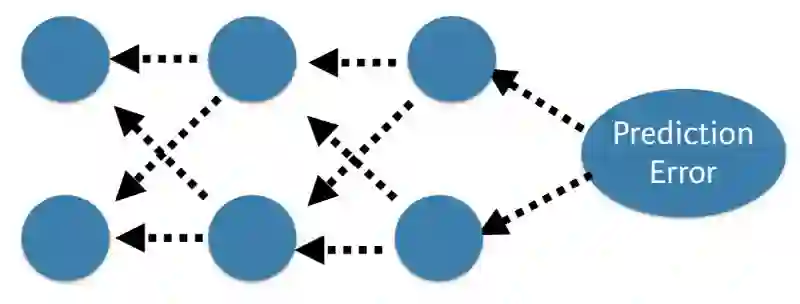
比较网络的预测值和期望输出，通过一个函数计算误差。接着在整个网络上反向传播误差，每次一层，权重根据其对误差的贡献作相应程度的更新。这称为反向传播（Back-Propagation）算法。在训练集的所有样本上重复这一过程。为整个训练数据集更新网络称为epoch。网络可能需要训练几十个、几百个、几千个epoch。

代价函数和梯度下降

代价函数衡量神经网络在给定的训练输入和期望输出上“有多好”。它也可能取决于权重或偏置等参数。

代价函数通常是标量，而不是向量，因为它评价的是网络的整体表现。使用梯度下降（Gradient Descent）优化算法，权重在每个epoch后增量更新。

比如，误差平方和（Sum of Squared Errors，SSE）就是一种常用的代价函数。

权重更新的幅度和方向通过计算代价梯度得出：

η为学习率

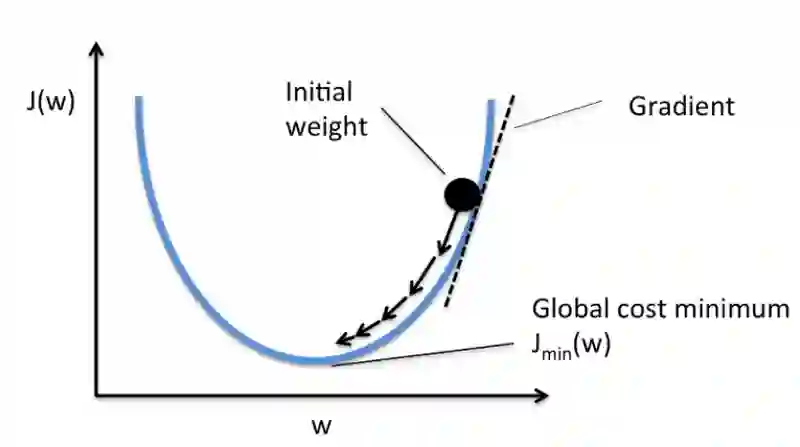
下为单个系数的代价函数梯度下降示意图：

多层感知器（前向传播）

多层感知器包含多层神经元，经常以前馈方式互相连接。每层中的每个神经元和下一层的神经元直接相连。在许多应用中，多层感知器使用sigmoid或ReLU激活函数。

现在让我们来看一个例子。给定账户和家庭成员作为输入，预测交易数。

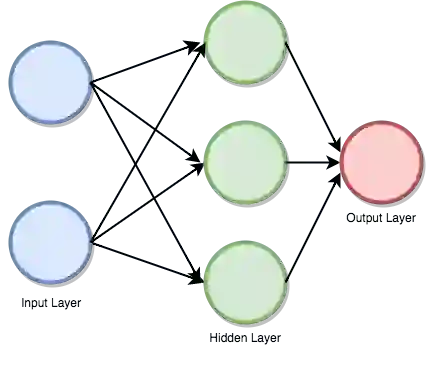
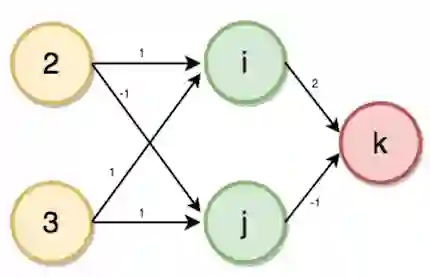
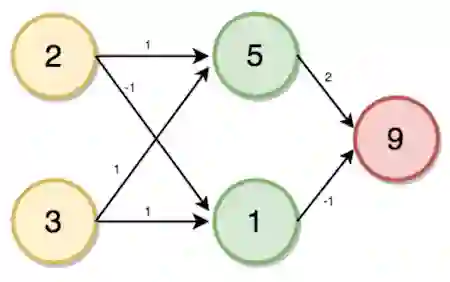
首先我们需要创建一个多层感知器或者前馈神经网络。我们的多层感知器将有一个输入层、一个隐藏层、一个输出层，其中，家庭成员数为2，账户数为3，如下图所示：

隐藏层（i、j）和输出层（k）的值将使用如下的前向传播过程计算：

i = (2 * 1) + (3 * 1) = 5
j = (2 * -1) + (3 * 1) = 1
k = (5 * 2) + (1 * -1) = 9

上面的计算过程没有涉及激活函数，实际上，为了充分发挥神经网络的预测能力，我们还需要使用激活函数，以引入非线性。

比如，使用ReLU激活函数：

这一次，我们的输入为[3, 4]，权重分别为[2, 4], [4, -5], [2, 7]。

i = (3 * 2) + (4 * 4) = 22
i = relu(22) = 22
j = (3 * 4) + (4 * -5) = -8
j = relu(-8) = 0
k = (22 * 2) + (0 * 7) = 44
k = relu(44) = 44

基于Keras开发神经网络

关于Keras

Keras是一个高层神经网络API，基于Python，可以在TensorFlow、CNTK、Theano上运行。（译者注：Theano已停止维护。）

运行以下命令可以使用pip安装keras：

sudo pip install keras

在Keras中实现深度学习程序的步骤

1. 加载数据

2. 定义模型

3. 编译模型

4. 训练模型

5. 评估模型

6. 整合

开发Keras模型

keras使用Dense类描述全连接层。我们可以通过相应的参数指定层中的神经元数目，初始化方法，以及激活函数。定义模型之后，我们可以编译（compile）模型。编译过程将调用后端框架，比如TensorFlow。之后我们将在数据上运行模型。我们通过调用模型的fit()方法在数据上训练模型。

from keras.models import Sequential
from keras.layers import Dense
import numpy
# 初始化随机数值
seed = 7
numpy.random.seed(seed)
# 加载数据集（PIMA糖尿病数据集）
dataset = numpy.loadtxt('datasets/pima-indians-diabetes.csv', delimiter=",")
X = dataset[:, 0:8]
Y = dataset[:, 8]
# 定义模型
model = Sequential()
model.add(Dense(16, input_dim=8, init='uniform', activation='relu'))
model.add(Dense(8, init='uniform', activation='relu'))
model.add(Dense(1, init='uniform', activation='sigmoid'))
# 编译模型
model.compile(loss='binary_crossentropy',
optimizer='adam', metrics=['accuracy'])
# 拟合模型
model.fit(X, Y, nb_epoch=150, batch_size=10)
# 评估
scores = model.evaluate(X, Y)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1] * 100))

输出：

$python keras_pima.py
768/768 [==============================] - 0s - loss: 0.6776 - acc: 0.6510
Epoch 2/150
768/768 [==============================] - 0s - loss: 0.6535 - acc: 0.6510
Epoch 3/150
768/768 [==============================] - 0s - loss: 0.6378 - acc: 0.6510
.
.
.
.
.
Epoch 149/150
768/768 [==============================] - 0s - loss: 0.4666 - acc: 0.7786
Epoch 150/150
768/768 [==============================] - 0s - loss: 0.4634 - acc: 0.773432/768 
[>.............................] - ETA: 0sacc: 77.73%

我们训练了150个epoch，最终达到了77.73%的精确度。

原文地址：https://towardsdatascience.com/deep-learning-with-python-703e26853820