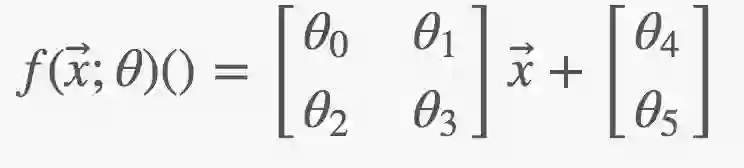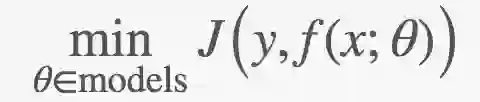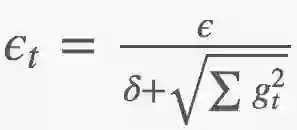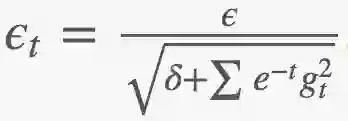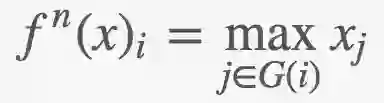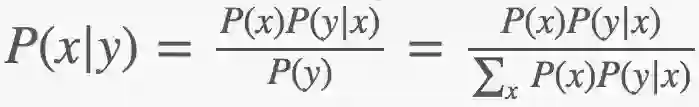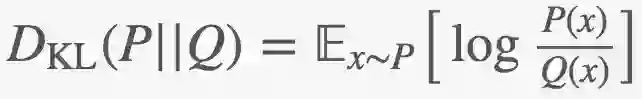深度学习入门笔记

会员服务 ·

深度学习入门笔记

2018 年 3 月 31 日 论智 randomekek

作者：randomekek

编译：weakish

编者按：开发者randomekek基于Ian Goodfellow《深度学习》（Deep Learing，“花书”）所做的笔记，供初学者大概了解深度学习包括哪些内容，或快速温习深度学习方面的知识，找到进一步学习的主题。

机器学习

机器学习（machine learning）是统计学的一个分支，使用样本逼近（approximate）函数。

我们有一个真底层函数或分布（distribution）生成了数据，但我们不知道它具体是什么。
我们可以在从训练数据中抽取的样本上尝试不同的函数。

图片标注的例子：

函数：f^*(图像) -> 描述
样本：数据 ∈(图像, 描述)
注意：由于存在许多合理的描述，描述是文本空间中的分布：描述 ~ 文本

机器学习的目标是找到满足以下条件的模型：

具有充分的表示能力以高度逼近真函数
具备使用训练数据寻找函数逼近的高效算法
逼近需要具有概括性，在未见（unseen）输入上能返回好的输出

机器学习的可能应用：

将输入转换为另一种形式——学习“信息”（information），提取并表示它。例如：图像分类、图像标注。
预测序列的缺失值或未来值——学习“因果”（causality），然后进行预测。
合成类似输出——学习“结构”（structure），然后进行生成。

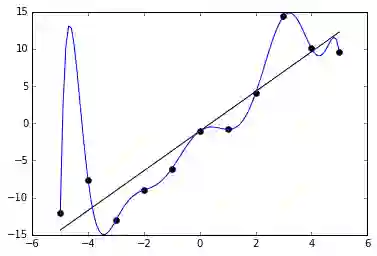
概括和过拟合

过拟合（overfitting）是指你找到了一个能够很好地拟合训练数据的模型，但这个模型不够概括。

例如：背下模拟测验答案的学习会在模拟测验上获得高分，但在期终测验中很可能会考砸。

一些折衷：

模型表示能力（representation capacity）：较弱的模型无法建模函数，但较强的模型更容易发生过拟合。
训练迭代（iteration）：训练过少没有给够拟合函数的时间，训练过多给了更多过拟合的时间。
你需要寻找弱模型和过拟合模型之间的中道。

交叉验证（cross validation）是标准技术：

留置一些从未训练过的数据用于之后的验证。
完成所有训练后，在留置数据上运行模型。
交叉验证之后你不能再调整模型了（当然你可以收集更多数据）。
如果模型训练分阶段进行，需要为每个阶段留置数据。

深度学习是机器学习技术的一个分支。它是一个强大的模型，在概括性方面也很成功。

前馈网络

前馈网络（feedforward network）用以下函数家族表示y = f^*(x)：

u = f(x; θ)

θ为模型参数。可能有几千个，也可能有几百万个θ₁...θ_T。
f是一个函数家族。f(x; θ)是一个在x上的单元函数。u为模型输出。
你可以想象一下，如果你选择了一个足够一般的函数家族，有很大的几率，其中一个与f^*相似。
例如：参数表示矩阵和向量：

设计输出层

最常见的输出层是：

f(x; M,b) = g(Mx + b)

参数θ用M和b表示。
线性部分Mx + b确保输出依赖于所有输入。
非线性部分g(.)让你可以拟合y的分布。
例如，输入是照片，输出分布可能是：

线性：y ∈ ℝ，例如照片的萌度
sigmoid: y ∈ [0, 1]，例如照片是猫的概率
softmax: y ∈ ℝ^C及∑ y = 1，例如，照片是C类猫中的一种的概率

为了确保g(x)拟合分布，你可以使用：

线性：g(x) = x
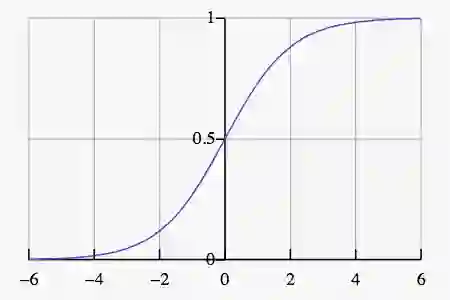
sigmoid: g(x) = 1/(1+e^−x)
softmax: g(x)_c = e^x_c/∑_ie^x_i

softmax实际上是欠约束的，而x₀常常设为1. 在这一情形下，sigmoid不过是有两个变量的softmax。
这是为何以上这些g函数是很好的选择背后的理论，不过还有很多其他不同的选择。

sigmoid函数图像

寻找θ

通过解决以下面向J的优化问题的成本函数（cost function）寻找θ：

深度学习成功的原因是有一个很好的算法家族来计算min.
这些算法是梯度下降（gradient descent）的变体：

theta = initial_random_values()
loop {
xs = fetch_inputs()
ys = fetch_outputs()
us = model(theta)(xs)
cost = J(ys, us)
if cost < threshold: exit;
theta = theta - gradient(cost)
}

从直观上说，在每个θ处，选择能最大程度上降低成本的方向。
这需要你计算梯度dcost/dθ_t.
你不希望梯度接近0，否则的话学得太慢了，也不希望梯度接近无穷，因为那是不稳定的。
这是一个贪婪算法，因此可能收敛到局部极小值（local minimum）。

选择成本函数

成本函数可能是任何函数：

误差的绝对值的总和：
J = ∑|y - u|
误差的平方的总和：
J = ∑(y - u)²
只要函数在分布一致时达到最小值，理论上就可以成为成本函数。

一个很好的想法是u表示y分布的参数。

理由：自然过程常常是模糊的，任何输入都可能具备某个范围内的输出。
这一方法同时给出了一个精确程度的平滑测量。
最大似然原则意味着：θ_ML = arg max_θ p(y; u)
因此我们希望最小化：J = -p(y; u)
对i个样本而言：J = -∏_ip(y_i;u)
两边取对数：J' = -∑_ilog p(y_i; u)
这就是交叉熵（cross-entropy）。

对y ~ Gaussian(center = u)（中心（均值）为u的高斯分布空间）应用以上想法：

p(y; u) = e^-(y-u)²
J = -∑log e^-(y-u)² = ∑(y−u)²
这就是平方总和是一个好选择背后的动机。

正则化

正则化（regularization）技术指试图减少概括性误差（generalization error）的方法。

它并不试图改善训练误差（training error）。

偏好较小的θ值：

给J加上某个θ的函数，我们可以鼓励较小的参数。
L²： J' = J + ∑|θ|²
L¹：J' = J + ∑|θ|
L⁰不是平滑的。
注意，对θ -> Mx + b而言，通常仅仅增加M。

数据增强（data augmentation）：

更多样本可以缓解过拟合。
同时考虑基于已有数据生成合理的新数据。
旋转、拉伸已有图像以创建新图像。
在x、网络层、参数中加入微小的噪声。

多任务学习（multi-task learning）：

在若干不同的任务间共享同一网络层。
迫使该网络层选择和通用任务集合相关的有用特征。

及早停止（early stopping）：

留置一个在训练中从未使用的验证集。
当验证集的成本停止下降时，停止训练。
你需要一个额外的测试集来真正地评估最终表现。

共享参数：

如果你了解你的数据的不变性，将其编码进你的参数选择。
例如，图像具有平移不变性，因此每个小块应该具有相同的参数。

dropout：

随机关闭网络层中的某些神经元。
神经元学习不理所应当地接受输入数据。

对抗（adversarial）：

通过在训练数据点附近生成对抗性数据，使得靠近训练数据点的点时常出现

深度前馈网络

深度前馈网络（deep feedforward network）：

u = f(x, θ) = f^N(...f¹(x; θ¹)...;θ^N)

该模型具有N层。

f¹...f^N-1：隐藏层（hidden layer）。
f^N：输出层。

深度模型听起来像是一个坏主意，因为它需要更多参数。
在实践中，它其实需要更少的参数，同时模型表现更佳。
一个可能的原因是每层学习数据的更高层的特征。
残差（residual）模型：
f'ⁿ(x) = fⁿ(x) + x^n-1

设计隐藏层

最常见的隐藏层为：

fⁿ(x) = g(Mx + b)

隐藏层的结构和输出层相同。
然而，在输出层上工作良好的g(.)在隐藏层上的表现并不好。
最简单也是最成功的g是线性整流函数（rectified linear unit，ReLU）：g(x) = max(0, x)

和sigmoid相比，当x非常大时，ReLU的梯度不会趋向0.

其他常用的非线性函数有Modulated ReLU：g(x) = max(0, x) + α min(0, x)

其中alpha为-1、非常小的值，或一个模型参数本身。
直觉是当x < 0时该函数仍有斜率。
在实践中，该函数和ReLU互有胜负。

maxout: g(x)_i = max_j∈G(i)x_j

G将区间[1..I]分成子集[1..m]、[m+1..2m]、[I-m..I].
比较一下，ReLU为ℝⁿ -> ℝⁿ，而maxout为ℝⁿ -> ℝ^n/m。
它是每组m输入的最大值，可以将它看成m段线性分区。

线性：g(x) = x

乘以下一层后，它等价于：fⁿ(x) = g'(NMx + b')
它是有用的，因为我们可以用它化简N和M，从而减少参数。

优化方法

我们使用的方法基于随机梯度下降（stochastic gradient descent）：

选择训练数据的一个子集（一个minibatch），由此计算梯度。
优势：不取决于训练集的尺寸，而取决于minibatch的尺寸。

有很多进行梯度下降的方法（下面用g表示梯度，用ϵ表示学习率，用Δ表示梯度更新）

AdaGrad —— 基于梯度量级减缓学习速度：
RMSProp —— 基于指数衰减的梯度量级减缓学习速度：
Adam —— 很复杂
梯度下降——使用梯度：Δ=ϵg
动量（momentum）：使用指数衰减梯度（exponential decayed gradient）：Δ = ϵ ∑ e^−tg_t
自适应学习率（adaptive learning rate），下面ϵ = ϵ_t：

牛顿法（Newton's method）：由于技术原因难以应用。
批量归一化（batch normalization）是进行如下变换的一个网络层：y = m(x-μ)/σ + b

m和b是可学习的，而μ和σ是均值和标准差。
这意味着层与层之间可以完全独立（前一层参数的调整不会影响当前层的分布）

课程学习（curriculum learning）：提供比较容易的内容供首先学习，接着加入难一点的内容。

简化网络

到目前为止，我们具备了足够的基础，可以设计和优化深度网络了。
然而，这些是非常通用和大型的模型。

如果你的网络有N层，每层有S输入/输出，那么参数空间（parameter space）为|θ|=O(NS²)。
这带来两个缺点：过拟合，更长的训练时间。

有很多缩减参数空间的方法：

寻找问题的对称性，选择具有对称不变性的层。
创建较低输出维度的层，网络必须总结信息至更紧凑的表示。

卷积网络

卷积网络（convolutional network）通过使用卷积（下文用星号表示卷积操作）取代矩阵乘法以简化某些层：

fⁿ(x) = g(θⁿ * x)

它用于空间分布（spatially distributed）的数据，包括一维、二维、三维数据。

一维：(θ ∗ x)_i = ∑_aθ_ax_i+a
二维：(θ * x)_ij = ∑_a∑_bθ_abx_ab+ij

它的基本思想（和精确的数学定义略有不同）是：每个数据点的输出是周围数据点的加权和。
好处：

θ为零时（i = 0附近的窗口w除外），刻画了位置概念。
刻画了平移不变性的概念，因为每个点的θ不变。
将模型的参数数目从O(S²)降低到O(w²)。

若有n层卷积，则基本值将可以影响wn半径内的输出。
实践中考虑：

用0补齐边缘。
平铺卷积（tiled convolution）（循环使用不同的卷积）

池化

经常与卷积网络配合使用的网络层是最大池化（max pooling）：

它的结构与maxout相同，一维情形下两者等价。
在高维情形下，G将输入空间分区为tile。
最大池化减少了输入数据的尺寸，可以看成是将输入的局部区域塌缩成总结。
最大池化同时提供了较小平移的不变性。

循环网络

循环网络（recurrent network）使用之前的输出作为输入，形成循环：

s^(t) = f(s^(t-1), x^(t); θ)

状态s包含过去的总结，而x是每步的输入。
循环网络比全动态（fully dynamic）模型简单：
s^(t) = d^(t)(x^(t), ... x⁽¹⁾; θ')

所有时间的θ都是一样的——循环网络假定时间不变性。
RNN可以学习任何输入长度，而全动态模型在不同的输入长度下需要不同的g.

输出：模型可能在每个时步（time step）返回y^(t)：

每步无输出，只关心最终状态。例：情感分析（sentiment analysis）
y^(t) = s^(t)，模型没有内部状态，因而不那么强大。但这样的模型更容易训练，因为训练数据y就是s.
y^(t) = o(s^(t))，使用一个输出层来转换（以及隐藏）内部状态。但训练起来更间接也更难。
一如既往，我们偏好将y看成一个分布的参数。

选择的输出可以被传回f作为额外输入，否则，y之间互相独立。

生成句子的时候，我们需要单词之间的条件依赖性，例如：A-A和B-B可能是合理的，A-B则可能不合理。

完成：

在x^(t) -> y^(t)的情形下，输入终结时结束。
额外输出y^(t)_end作为输出完成的概率。
额外输出y^(t)_length，剩余/总输出长度。

基于同样的梯度下降类方法优化。

通过将循环展开成一个扁平的公式计算梯度，这称为沿时间反向传播（backpropagation through time，BPTT）。

BPTT的一个难点是梯度Δ = ∂/(∂s^t)：

Δ > 0：状态爆炸，提供了不稳定的梯度。解决方案是在下降过程中裁剪梯度更新至一个合理的尺寸。
Δ ≈ 0：这让状态可以在较长时间内保持，然而梯度下降方法需要梯度才能工作。
Δ < 0：RNN处于持续损失信息的状态。

有一些RNN的变体施加了简单的先验以帮助维持状态s^(t) ≈ s^(t-1)：

s^(t) = f_ts^(t-1)+f(...)：我们可直接得到一阶导数∂/∂x
它让我们传递之前步骤的梯度，即使f本身梯度为零。

长短时记忆（long short-term memory，LSTM）建模输入、输出和遗忘：
s^(t) = f_ts^(t-1) + i_tf(s^(t-1),x^(t);θ)

输出：y^(t) = o_ts^(t)
LSTM使用概率（称为阀门（gate））：o_t 输出，f_t 遗忘，i_t 输入。
阀门通常是sigmoid层：
o_t = g(Mx + b) = 1/(1+e^Mx+b)
生成新数据（g）和使用它作为长期信息（i）是解耦的，因而我们得以保留长期信息。
因为过去和未来之间有直接的连接，所以更多地保留了梯度。

门控循环单元（gated recurrent unit, GRU）是一个较简单的模型：
s^(t) = (1-u_t)s^(t-1) + u_tf(r_ts^(t-1), x^(t); θ)

阀门：u_t 更新，r_t 重置。
LSTM和GRU互有胜负。

循环网络的dropout偏好d(f(s,x; θ))（不储存信息），而不是d(s)（损失信息）。
记忆网络（memory network）和关注机制（attention mechanism）。

数据集的用途

输入数据的类别非常广，深度学习可以应用的地方很多。
图像向量[0-1]^WH：图像到标签，图像到描述。
基于每个时间切片的音频向量：语音到文本。
文本嵌入词汇向量[0-1]^N：翻译。
知识图：问题回答。

自动编码器

自动编码器（autoencoder）包含两个函数，从输入空间到表示空间（representation space）的编码函数f和解码函数g. 目标函数为：

J = L(x, g(f(x)))

L是损失函数（loss function），当图像相似时，L的值较低。
想法是表示空间学习重要的特征。
有一些额外的正则化工具以防止过拟合：

稀疏自动编码器（sparse autoencoder）最小化J' = J + S(f(x))。这是表示空间上的正则化。
降噪自动编码器（denoising autoencoder）最小化J = L(x, g(f(n(x))))，其中n加入噪声，迫使网络区分噪声和信号。
收缩自动编码器（contractive autoencoder）最小化J' = J + ∑ ∂f/∂x，迫使编码器变得平滑：相似的输入得到相似的输出。
预测自动编码器（predictive autoencoder）最小化J = L(x, g(h)) + L'(h, f(x))。预测自动编码器不同时优化g和h，而是交替优化两者。