EMNLP 最佳论文解读:来自信息瓶颈的新语言学理论
关于信息瓶颈理论,之前也就稍微了解一些,没具体深入,结果为了看这篇论文,又好好补了补,才慢慢理解了这篇论文让人惊喜的地方。
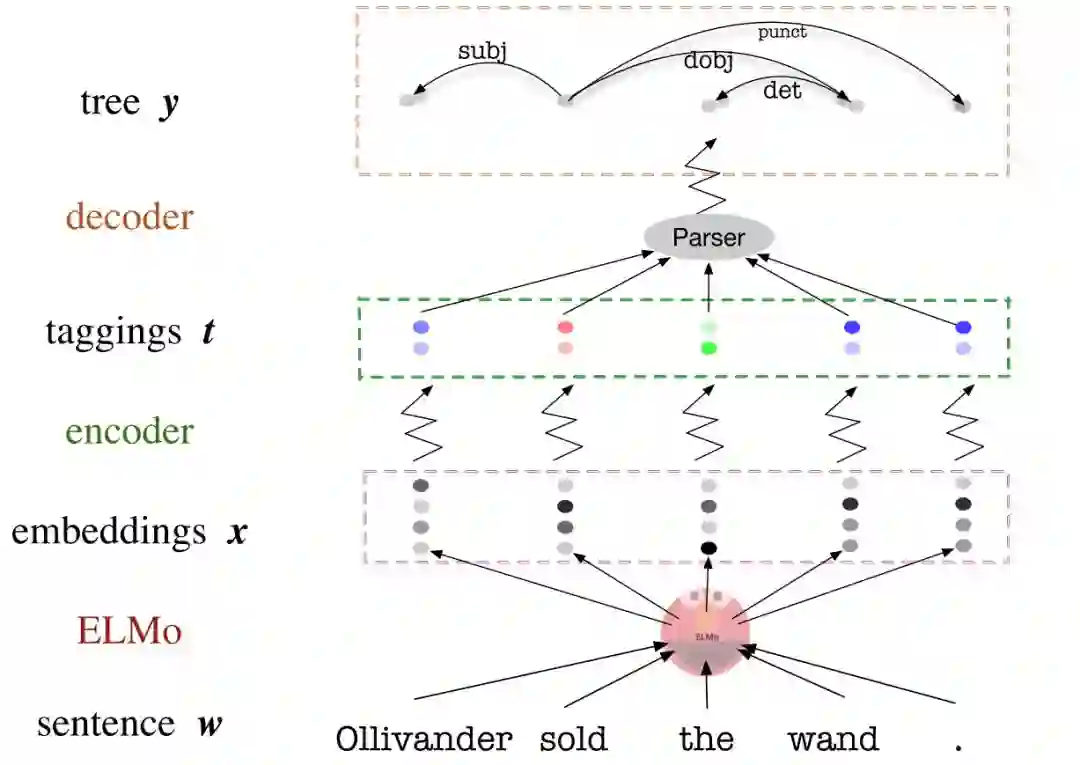
variational information bottleneck (变分信息瓶颈,VIB)法非线性地压缩预训练词向量,如 ELMo 或 BERT,让它们只包含能够帮组判别式语法分析器(parser)的信息。“ 也就是说用 VIB 法对预训练词向量进行了压缩,只保留之后语法分析所需的信息。
关于语法分析(Parsing),是 NLP 中的一个主要任务,找出句子中词之间语法关系的任务,这里只是作为一个实际用例,并不是重点。
然后就是论文中最关键技术,信息瓶颈(information bottleneck),最早由 Naftali Tishby 在1999年提出的信息论理论,之后在 2015 年,将这个理论推广到深度学习领域,用来解释深层神经网络。之后在其演讲中,因为得到 Hinton 一句:”我要听 10000 遍才搞懂!“,一下就出名了。
所以先解释一下信息瓶颈吧,懂的人可以直接跳到结论。
Information Bottleneck
首先信息瓶颈里涉及的几个概念,也是信息论主要讨论的问题之一,如何将信息最大程度压缩,然后又还原出想要的信息。先是压缩(compression),即将一段信息,比如图片或文本,用更精简方式表示,通常需要编码(Code)的辅助。
于是信息瓶颈中对信息处理的整个过程就是,先拿到信息,然后压缩编码(encode)成更短更有效表示,之后存储或传输这些表示,当需要的时候就解码(decode)获得原来想要的信息。
然而在压缩前,需要先明确一个问题,哪些信息才是真正需要的。这样才能够明确压缩时,哪些信息可以舍弃。在信息瓶颈中,我们希望做的是,在尽可能压缩原信息同时,又能尽量只保留想要的信息。其实也就是 Tishby 说的学习的本质是遗忘。
举个例子,有一段手写文字,需判断是谁写的。
假设写这个的人是 Y,写下来的这个样本是 X。现在假设先拍张照片,称这个照片为样本的一个函数 T(X),这张照片足够清晰,能通过笔迹分析确定是 Y 写的。那么称 T(X) 是 X 对 Y 的充分统计量(sufficient statistic),T(X) 几乎捕获了 Y 手写的所有信息。而如果同时,用一个识别系统识别 X 后,自动生成电子文本,称其为 U(X),那么 从 U(X) 就很难判断是谁写的 X,此时称 U(X) 不是 X 用来预测 Y的充分统计量.
充分统计量可以有很多种,而有时需要的是其中最小充分统计量,M(X)。即 M(X) 是 X 的充分统计量,但同时只用了尽量少的比特。拿手写文字来说,可能写这个的人,写某些字母非常有特点,只要确定这些字母就知道是他,那么就可以只拍这两个字母的照片,显然这比之前 T(X) 需要的比特数更少。
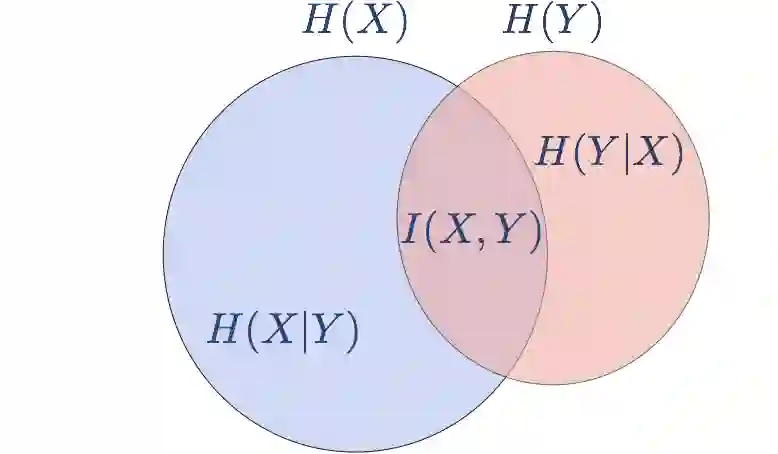
那么怎样正式表示以上概念呢,先引入信息论中一个很重要的概念,互信息(Mutual Information),它表示两个随机变量共享的信息。如果随机变量 X 没有任何关于随机变量 Y 的信息,那么称它们互信息为 0,举个例子,抛硬币两次,即使你知道第一次出了什么,但对第二次也没有影响。而另一个例子是,一叠扑克牌,如果你翻开第一张是”红桃K“,那么你很明显就获得了你要翻开第二张牌的一些信息,如果是一副普通扑克牌的话,它就不可能是“红桃K”。
说完互信息,就获得了挑战信息瓶颈理论所需的所有理论。信息瓶颈理论称,如果有输入随机变量 X,以及一个相关的随机向量 Y,我们的目标是学习一个 p(t|x),X 到某个压缩表示 T 的映射,那么需要做的是最小化下式:
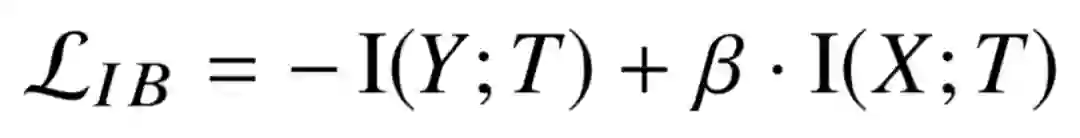
直观理解就是最大化 T 和 Y 之间互信息同时,最小化 T 和 X 之间的互信息。而通俗点讲,就是前面说的只保留 T 中对预测 Y 有用的信息,去除 T 中来自 X 的不相关信息。这里的 beta 系数,主要是用来控制这两个互信息之间的平衡,当 beta 大就是希望更多压缩,当 beta 小则希望保留更多 X 中信息。
回到论文
于是论文就是要完成上述公式的计算,需要先明确变量,X 即 ELMo 产生的上下文词向量,Y 在这里就是依存关系。T 还有它与 X,Y 互信息的获取就成了关键。
对于信息瓶颈实现,论文中用到的是 VIB 技术,前面加了 Variational (变分),其实无论 VIB 还是 VAE (Variational AutoEncoder) 这样前面加上 Variational 的。其实就是就是假设了一个变分分布来进行拟合需要获得的分布。
在计算互信息 I(X;T) 时,根据定义:
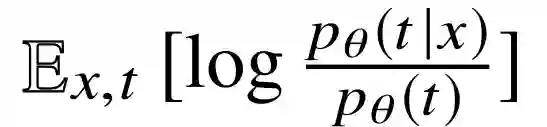
上面的 p(t|x) 由模型中参数定义,而 p(t) 获取很麻烦,这时可以将它替换成一个变分分布 r(t),替换之后根据下式:
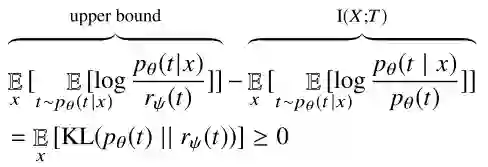
因为 KL 只能为非负,所以相当于设置了 I(X;T) 的一个上界。之后就只用优化替换后的式子,也就是上界,而进一步转换后其实就相当于只用优化 KL 距离
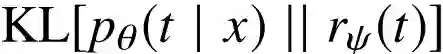
于是就获得 IB 公式中 I(X;T) 的计算方法,这一部分用编码解码里的说法,也可称为 Token Encoder。关于具体实现,文中探索了两种不同的 T,分别压缩成离散的标签(discrete tag)和连续的向量(continuous vector)。
对于离散标签,直接用一个前向网络获得 k 个输出,然后再用 softmax 获得一个分布,取最大的。而连续向量,则是假定 t 是一个 d 维的高斯分布,然后用前向网络从 ELMo 的词向量获得一个 2d 维的输出,上半部分作为均值,下半部分作为方差。以上操作都是分别对 ELMo 单个词向量进行的操作,因为这篇论文的目的就是探索词向量中的语法信息。
接着是 I(Y;T) 的计算:
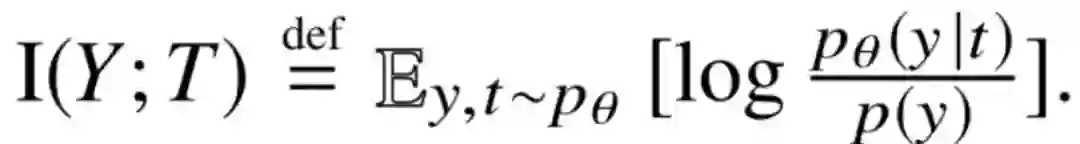
因为 p(y) 与需优化参数无关,所以可当作常量在之后计算忽略。我们目的是让 p(y|t)尽量大,直接计算的话也很麻烦,所以将 p(y|t) 替换成一个变分估计 q(y|t),然后根据 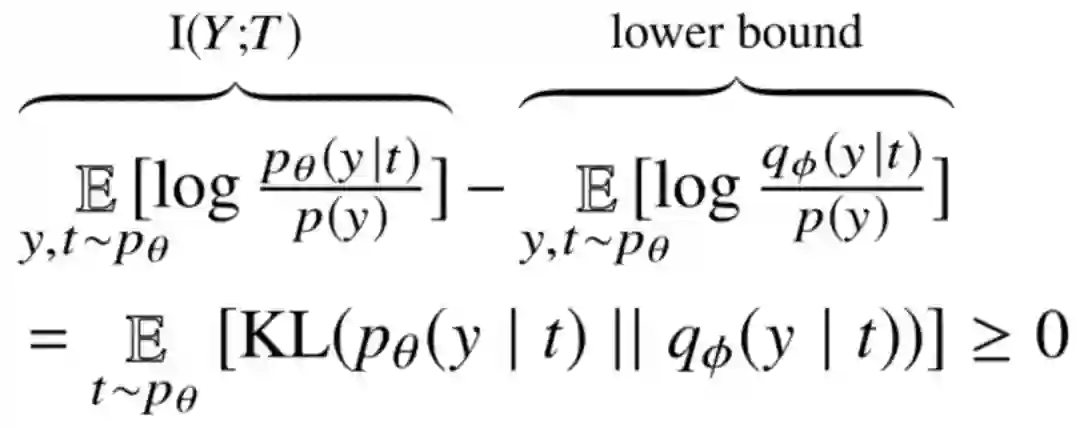
相当于设置了一个下界,计算时,可以直接用基于采样的估算法来估计 log q(y|t)。而这整个过程相当于,从 x 获得压缩的 t,然后希望训练的分析器能在平均期望上给 x 对应的 y 分配高的 log q(y|t) 值。
具体实现,用 deep biaffine 依存分析器来作为 q(y|t),关于 deep biaffine 可参考 Manning 的课或论文。获得了大概关于 y 的估计之后,可通过 Edmonds 的 directed spanning tree algorithm 算法获得更精确依存关系。
现在就获得了 IB 方程中的全部项,但文中为了避免 I(X;T) 只用 X 中对应的上下文信息,就多加了一项:
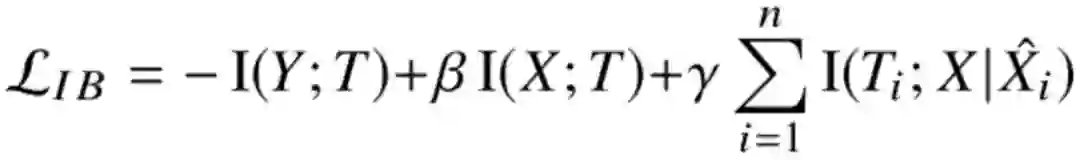
其实就是用 ELMo 词向量表中的向量直接来估计 T,希望通过该方式强迫 T 利用 X 对应词本身的信息。虽然想法是好的,但实际实验表明该项用处貌似并不大。
有意思的结论
这篇论文最有意思的应该是在结论方面了,结论分为离散标签和连续向量两个部分。
对于获得的离散标签,通过直接用于预测 POS 标签,分析发现其中已包含了大量的 POS 信息。其实也说明了人类本身对语言分析直觉的正确性。
但当作者们用获得的离散标签和句子本身的 POS 标签,来同时预测依存时,却发现压缩获得的离散标签更优于 POS 标签。这就意味着通过这样的压缩,模型找到了一种比 POS 更优的标签来用于依存分析。就像 AlphaGO 发现了一种更优的,人类从没有开辟过的下法一样。
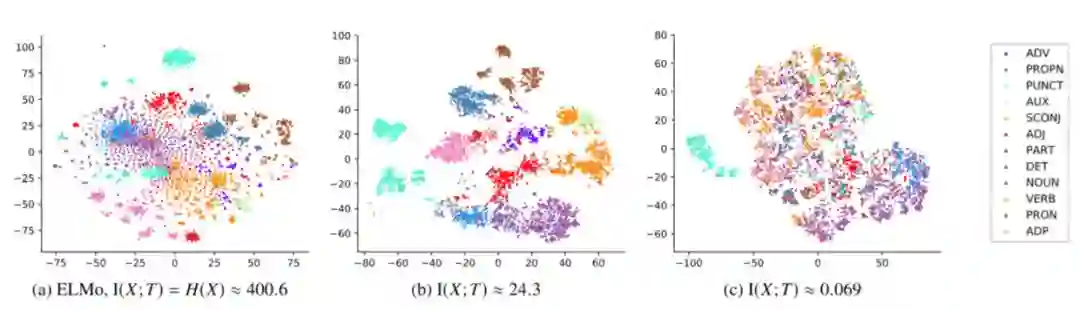
对于连续向量,作者们探索了不同压缩比例下,获得向量对后续依存任务的影响,发现压缩比在一定程度的压缩会让结果更好。通过可视化向量点和其对应的 POS 标签,也会发现,压缩比一定时的分离效果会更好。
之后将该方法和其他的压缩方法对比,发现 VIB 也基本上占优。
此外,文中还对压缩后的向量进行分析,发现通过语义分析任务的压缩,词向量保留下来的确实只有语法(syntact)相关的信息了,而语义相关的信息如词干(Stem)的信息随着压缩比增大,都被去除掉了。
其实我感觉这篇论文最有意思的地方倒不是性能方面,而是压缩之后的分析,正如这里用依存分析获得了一套针对依存分析的标签,完全可将 IB 中解码器部分替换成其他任务,亦或者是多个 NLP 任务,通过该方法或许就可以建立一套相对目前语言学理论更优的标签体系。
Reference
[1] Anatomize Deep Learning with Information Theory
[2] Information Bottleneck theory for Deep Learning
[3] New Theory Cracks Open the Black Box of Deep Learning
[4] A DEBATE: THE INFORMATION BOTTLENECK THEORY FOR DNNS(非常推荐)
本文转载自公众号:安迪的写作间,作者:Andy
推荐阅读
T5 模型:NLP Text-to-Text 预训练模型超大规模探索
BERT 瘦身之路:Distillation,Quantization,Pruning
Transformer (变形金刚,大雾) 三部曲:RNN 的继承者
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLP君微信(id:AINLP2),备注工作/研究方向+加群目的。