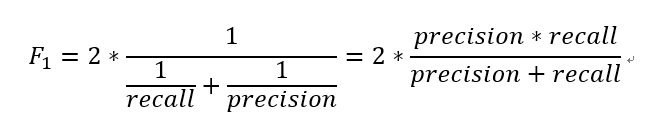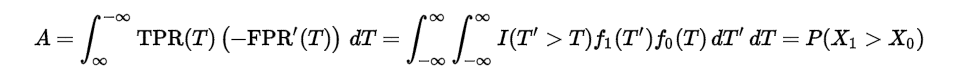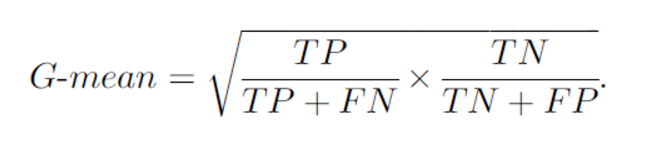[机器的机器在学习] 你有一次国庆节大作业待接收~

[点击蓝字，一键关注~]

明天就国庆放假了，正好赶上中秋节，首先祝大家“双节”快乐！ 不管是出去玩，还在一个人在家里，在宿舍，在自己的小房子“玩”，祝大家都能找到自己的乐趣！但是呢， 安全第一！ 想乘着国庆好好学习一把的童鞋， 也别太拼， 学习一会儿就休息一下。然后我想说，我国庆要出去“嗨”一下了，so 这期间不能更新了。。

==============================

好，接下来我们聊一下机器学习中的一个基本概念，混淆矩阵，confusion matrix，第一个听说混淆矩阵的时候，稀里糊涂的看不懂，等到我明白了机器学习中做分类问题是怎么一回事的时候，渐渐就明白了，为什么会有混淆矩阵。

首先简单说下分类问题，曾今听说过，我们生活中分类是无处不在的，我们每天的生活其实就是在做分类。就比如说我们找工作，自己心里边会对不同公司做个分类，然后选择自己喜欢的那个class。然而限于我们身处象牙塔的童鞋见识，对社会的了解，更具体的对某家公司的了解，可能本来人家是一个很牛逼的公司，然后你都不知道，错误的把人家归类到普通公司了，这就说明你分类分错 了。但是肯定有些公司你是不会分错类的，比如BATJ。。。

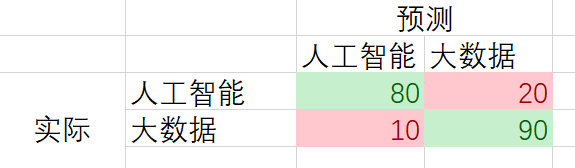
好，然后我们用稍微正式点语言描述一下，假设现在教室里有200个同学，按专业分，有2个专业的同学，比如人工智能专业和大数据专业，每个专业都是100名同学。假设他们都是随意坐在教室里， 然后我们在教室中间划一条线（分类器），这样就把200名同学分为了2类。然后发现左边有20名人工智能专业和20名大数据专业的学生，右边有10名人工智能学生和90名大数据专业的学生。然后我们这个最后统计的数据写在一个矩阵里面，如下，这个矩阵就叫混淆矩阵，然后我们解释一下。

先看人工智能专业，实际有100个同学，然后分类器分类之后得到的结果是80名同学都归到了左边，表示分类正确，有20名同学分到右边，表示分类错误。同理大数据专业，有10名同学分类到左边，表示分类错误，有90名同学归到右边，表示分类正确。

然后用稍微专业的术语给大家介绍一下。

TP：实际是正类，预测为正类（预测正确）

FN：实际是正类，预测为负类（预测错误）

FP：实际是负类，预测为正类（预测错误）

TN：实际是负类，预测为负类（预测正确）

 

相关术语：

不管是正类还负类，都有预测正确的部分，然后把两类预测正确的加起来除以总共的人数，就叫准确率,Accuracy Rate。

Accuracy Rate(准确率)  =  (TP+TN)/(TP+TN+FN+FP)  =(80+90)/200=85%

同理，正类和负类都有预测错误的样本，错误的加起来除以总人数，就叫误分率，Error Rate。 

Error Rate(误分率)  =  (FN+FP)/(TP+TN+FN+FP) =(10+20)/200=15%=1-准确率

        

上面两个是一个总体的概念，对分类问题的全局而言的。然后对于实际为正类的样本中，预测也为正类（有一部分正类预测为了负类）的样本所占的比例叫做Recall。

Recall(召回率)   =  TP/(TP+FN) = 80/100=80%

同理，对于预测为正类的样本中，实际也为正类的样本所占的比例叫做Precision。

Precision(查准率)  =  TP/(TP+FP) =80/（80+10）=88.9%

上面两个是对预测正确而言的，不管是正类还是负类。

那么预测错误的占比怎么表示呢，通过上面几个公式也许大家发现了，其实就是从两个维度分别去考虑，然后就可以表示成不同的表达方式，或者叫度量标准。好，再说两个概念，我们把实际为负类，预测为正类的样本占所有实际为负类的比例叫做False Acceptance Rate或者False Positive Rate

FAR(False Acceptance Rate)=FP/(FP+TN) =10/（10+90）=10%

实际为正类的的样本中被预测为负类的样本所占的比例叫做False Positive Rate。

FRR(False Positive  Rate)  =  FN/(TP+FN) = 20/(80 + 10) = 22.2%

那么有了False Positive Rate，肯定就会有True Positive Rete，其实这个就是Recall。

   True Positive Rete  =  TP/(TP+FN)   =  80/100=80%

好，到这里基本概念就都差不多了，然后通过混淆矩阵，还有几个周边的概念，大家必须要去了解的东西，比如F1值，ROC，AUC等，最后还有一个不平衡分类问题，怎么去度量？

Let’s Go On...

F1值：F1值也叫F1 score， F1 measure，公式为：

            = 2*（88.9%*80%）/（88.9%+80%）=84.2%

F1值计算不难，重要的是理解他的物理意义，F1将recall和precision合并为一个公式，这样做的好处是可以对比不同模型之间的分类的性能。因为当我们不能通过两个模型的Recall和Precision来做出评价的时候，F1值就派上用场了。

ROC曲线：ROC曲线是一条曲线，既然是一条线，那我们怎么画出来呢？一般来说在二维平面内画一条曲线，需要知道横坐标和纵坐标，高中学的五点作图法，对吧。然后我想问下大家，我们定义一个分类模型，是不是一下就得到了混淆矩阵了？专业点说就是我们可以得到混淆矩阵的个数是离散值还是连续值？很明显是连续值。不然也不用机器那么机智的去学习了。

好，如果你能明白我上面在说什么，那么ROC曲线就不难画出来了。只需要明白ROC曲线的横坐标是False Positive  Rate，纵坐标是 True Positive Rete即可！

有了ROC曲线，AUC就更不难理解了，AUC表示ROC曲线与坐标轴围成的面积，求个积分就行了吧，AUC值越大，表示分类器的性能更好！

AUC的计算公式如下

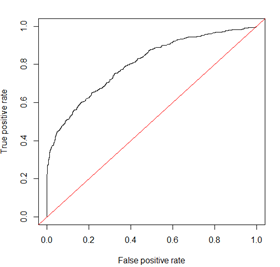
下面这个图就是ROC曲线，红色线表示AUC=0.5的时候ROC曲线的样子。然后这里要提一下基尼系数，因为Gini=2*AUC-1，从图中看，Gini系数指ROC曲线与红色线围成的面积占AUC的比例。基尼系数本来是经济学中的一个概念，基尼系数为0，表示没有贫富差距，基尼系数越大，表示贫富差距越大。

好，到这里我们基本说完了混淆矩阵周边的所有概念，那是不可能的。。。。

接下来的问题是对于不平衡数据来说，对于上面我们讨论的问题说的是人工智能专业和大数据专业都是100名同学，这种分类问题，是常见的二分类问题，如果我们的正类有199个，负类样本有1，然后做分类的时候，上面讲的那些公式基本都废了。。。是的，不信大家可以去试试计算一下。然后最后我要介绍另外一个公式叫G-means，G-means是一种常用的评价不平衡问题的度量准则，公式如下：

好，混淆矩阵周边就介绍到这里了，在写的过程中，我发现这些看似简单的东西，其实其中还有很多的学问，希望大家可以仔细体会一下，然后对自己不懂的东西再多研究研究，搞清楚每个公式的是什么，以及怎么用？