[有意思的数学]假设检验

 

最近工作的事情，加上论文开题，忙的半死，好久没更新了，再不更新，我怕大家会忘记我了。说好的概率统计还有两三次，今天说一下假设检验。

 

假设检验的意思其实检验一个事先定义的假设。这个假设一般指的是对于总体参数的假设，比如常用的均值和方差。为什么要假设呢，直接算出来不就好了？总体太多了，算不出来，或者算出来需要消耗很多的人力，物力。比如我们假设总体均值为100，那么通过抽样得到一个总体的样本，然后根据样本信息，去推断总体均值是不是100。这里推断的过程就是检验的过程。所以说假设检验和参数估计一样，也是一种统计推断的方法。参数估计是从样本信息或者利用先验信息去直接计算总体信息，而假设检验是事先假定总体信息的值为某个固定的值，然后根据样本信息去推断，如果总体信息的值是那样的话，能不能抽到这样一个样本，这就是假设检验。

以上就是假设检验的基本思想，下面把几个问题解释一下。

# 原假设和备择假设

一般把关于总体分布的某个命题称为假设。假设分为原假设和备择假设，原假设和备择假设是相依相存的关系，如果没有备择假设，也就无所谓原假设，反之亦然。这里需要注意的就是怎么确定什么样的命题作为原假设，而什么样的命题作为备择假设。这个问题一般要根据具体假设的问题不同而不同。一般方法是把没有把握不能轻易肯定的命题作为备择假设，而把没有如果没有非常充分的理由就不能轻易否定的命题作为原假设。从这个可以理解一下，我们做假设检验的目的是验证原假设是不是正确，对于拒绝一个原假设或者不拒绝（不等于接受）原假设，都需要一个充分的理由。举个栗子，比如某某工厂生产一批产品，每天的产量均值是10000，然后买了一批新设备，现在的产量是10100，厂长想分析一下是不是新设备对产品产量的增加有影响。那么我们的原假设就应该是购买新设备之前的产量。因为我们只能通过几天的采样来判断总体的均值，我们的推断是不充分的，所以没有非常充分的理由去接受产量在增加。

 

# 去真错误和取伪错误

去真错误和取伪错误也叫第一类错误和第二类错误。去真和取伪都是相对于原假设而言的，就是说如果原假设是正确的，是一个真命题，而我们拒绝了原假设，那就犯了去真错误。一般样本的都是随机获得的，存在随机性，所以每次采样都是不同的，那么可以得到的样本信息就是随机的，这里的样本信息一般就是指的样本平均值，样本方差等。然后根据样本信息会得到拒绝域，如果样本刚好落入拒绝域，则就会发生去真错误，当然这里前提是原假设为真。那我怎么知道原假设是不是真的呢？这个是不能知道的，无论犯什么错误，都是一个概率值而已。而如果原假设为假，而我们没有拒绝，那就犯了取伪错误。

建立一个比较好的假设检验的目标是使两类错误都尽可能的小，但是事实是很难达到他俩同时减小。也不是没有办法，办法是增加样本容量，但是增加样本就会带来抽样的成本增加。

 

# 检验水平

说到水平，一般是用来衡量某个问题的质量。比如有人说你玩游戏水平不行啊，意思就是说你比较菜，质量不高。那么对于一个检验来说，检验水平就是用来衡量检验结果的可靠程度的一个指标。在一个具体的问题中，把犯去真错误的概率叫做检验水平。那大家想一下，检验水平越高越好，还是越低越好？

通常来说，我们肯定是希望犯错误的概率尽可能的小，也就是说比如0.01肯定比0.05好。能不犯错误，尽量别犯错误。但是这样的话，也就是说检验水平的值越小，检验的“水平”是越高的。

 

# 参数检验和非参数检验

参数检验就是检验参数，要检验参数，前提是知道总体的参数吧，要知道总体的参数，就需要知道总体的分布。也就是说，如果不知道总体的分布，就没法做参数检验，也就是可以做非参数的检验。他们的关系就是这样。

 

# 双边检验和单边检验

双边和单边的区别主要在于拒绝域的形式，拒绝域说白了其实就是一个区间，区间的概念大家应该都知道。如果拒绝域是一个区间，就是单边检验，如果是两个区间，就是双边检验。

 

# 单样本检验和双样本检验

这个是针对样本是由几个总体得到而决定的，其实主要是看所研究问题的不同而区别的。比如两个总体的均值差，方差比之类的检验，必然涉及两个总体，这样的检验就是双样本检验，反之单样本检验。

 

# 正态总体的假设检验

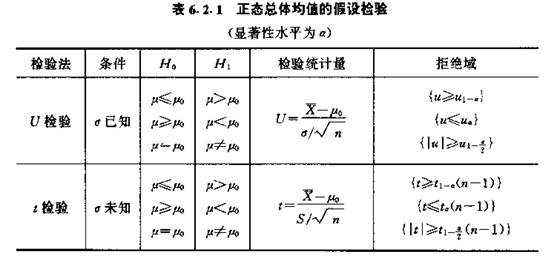
到这里，假设检验的问题，基本已经结束了。而正态总体的假设检验，只是一个具体的应用栗子了。对于正态总体来说，主要是总体均值和方差的检验，下面给大家贴两个表格吧，来源是茆诗松老师的概率论与数理统计（第三版）。对应与总体方差已知和未知，分为u检验和t检验。而检验统计量的理论基础的三大分布，有兴趣的童鞋可以自己去看看。没兴趣看看表格就好了，重要的是怎么用程序来把这个实现一下。

# 最后两个总体的假设检验就留给大家自己去学习了

祝大家玩的愉快！