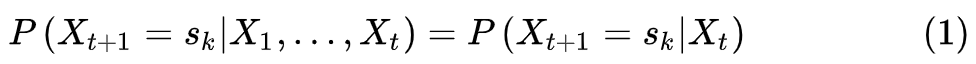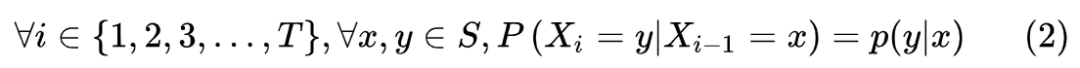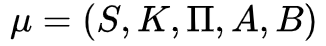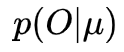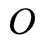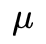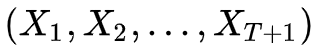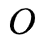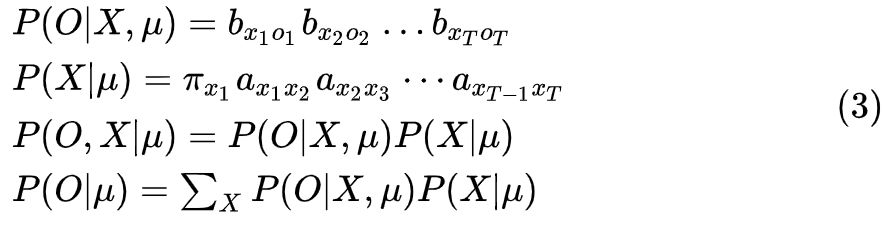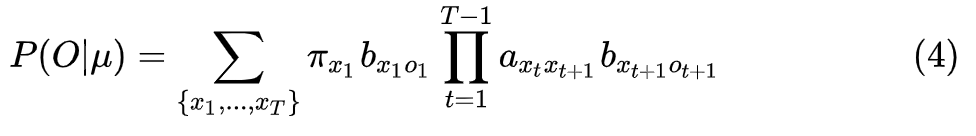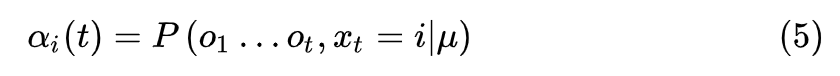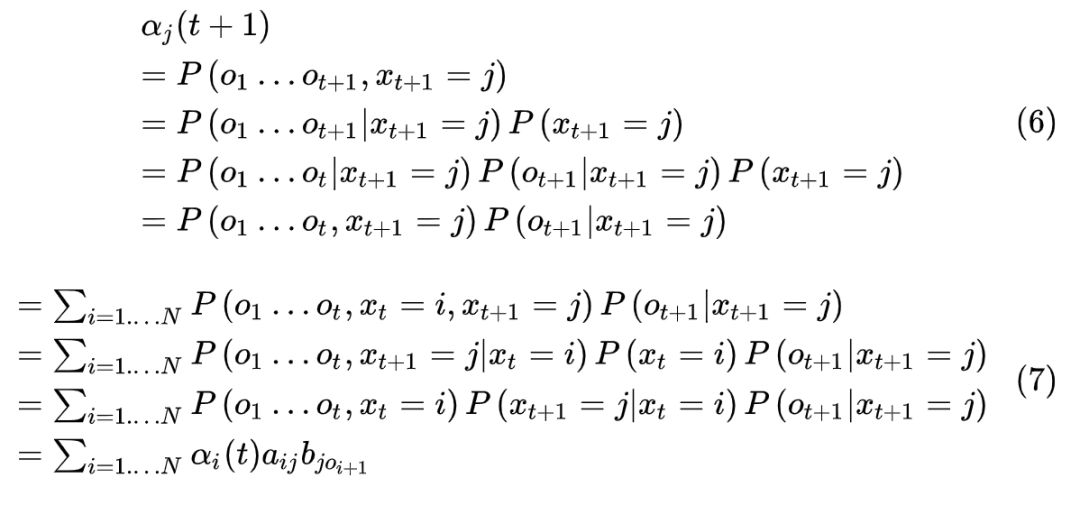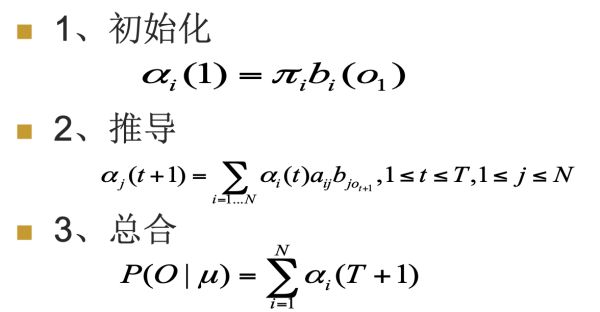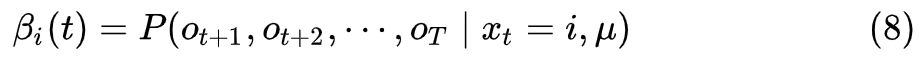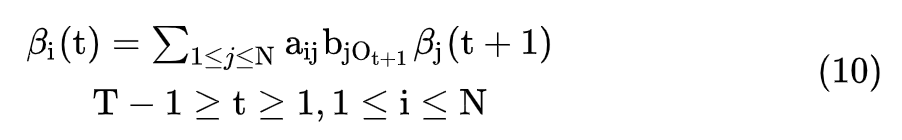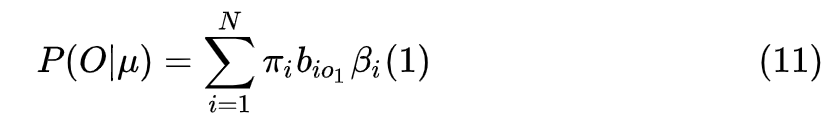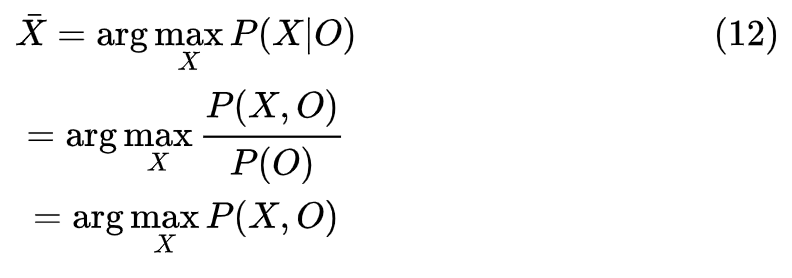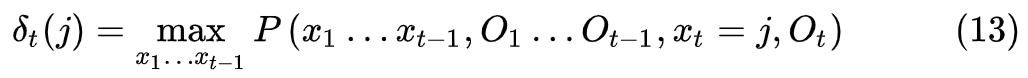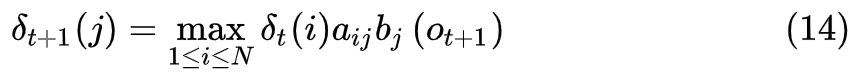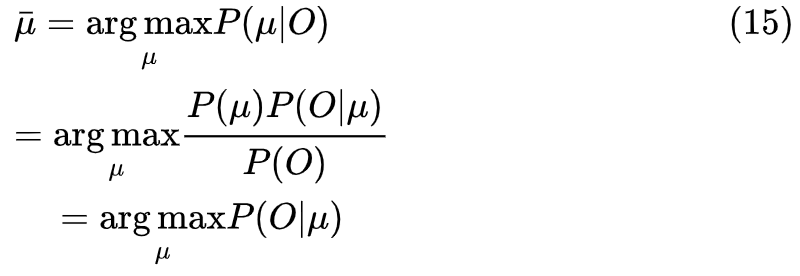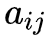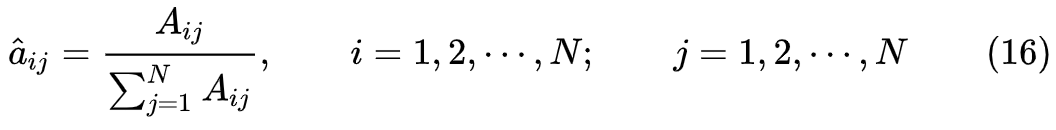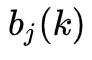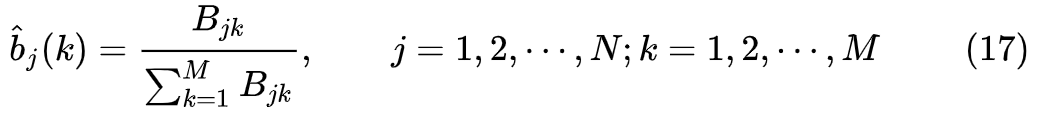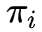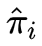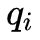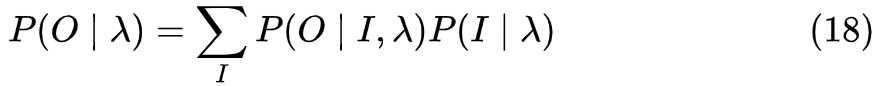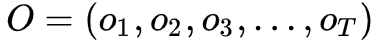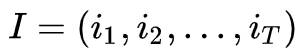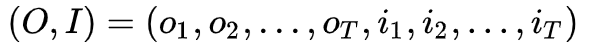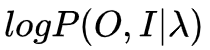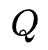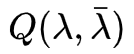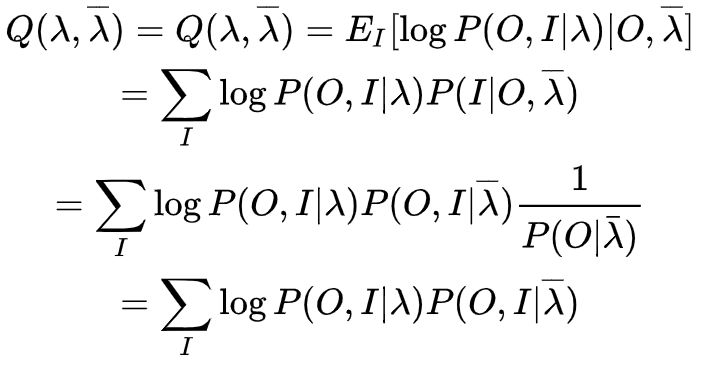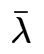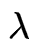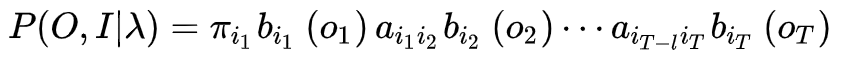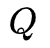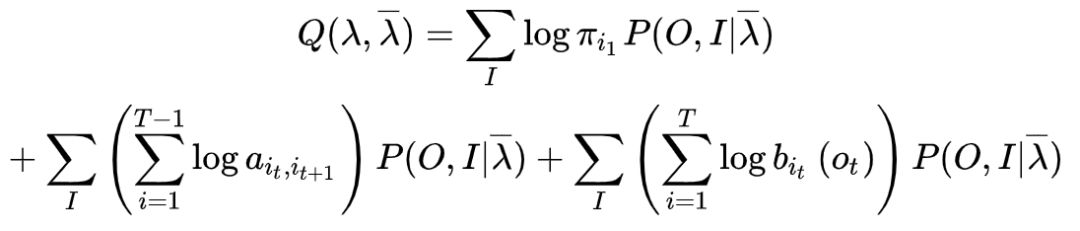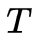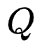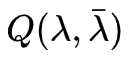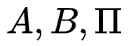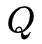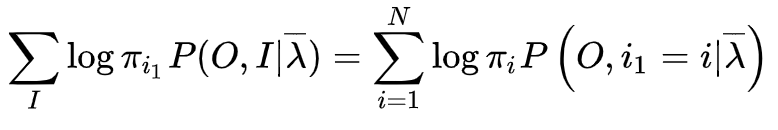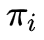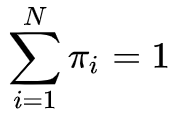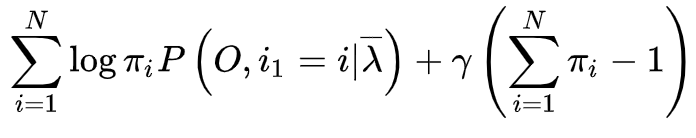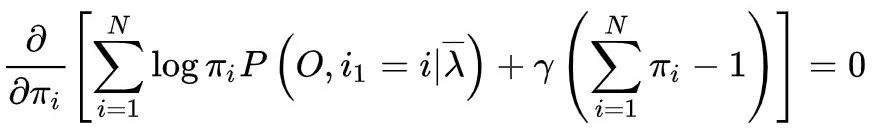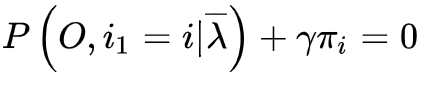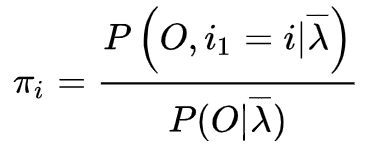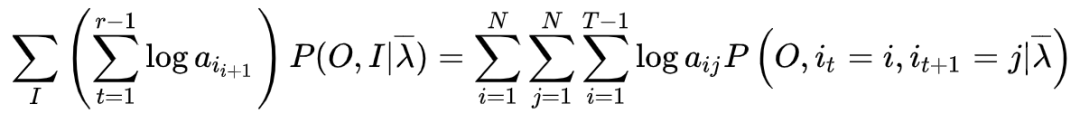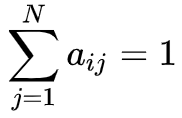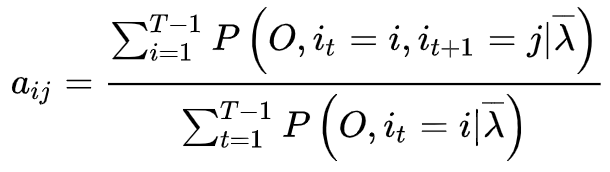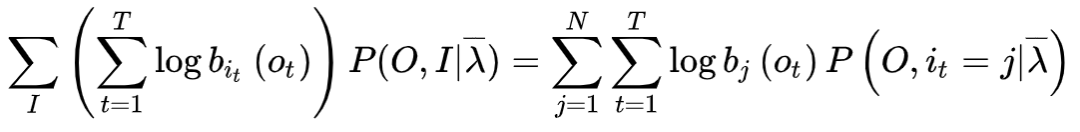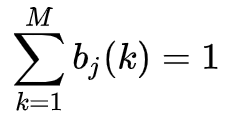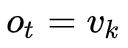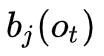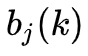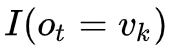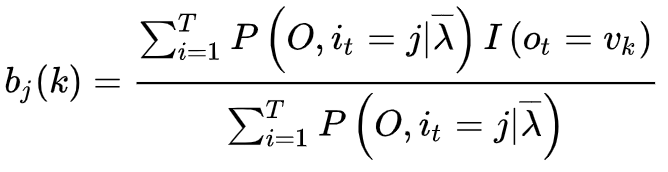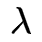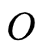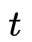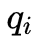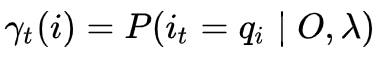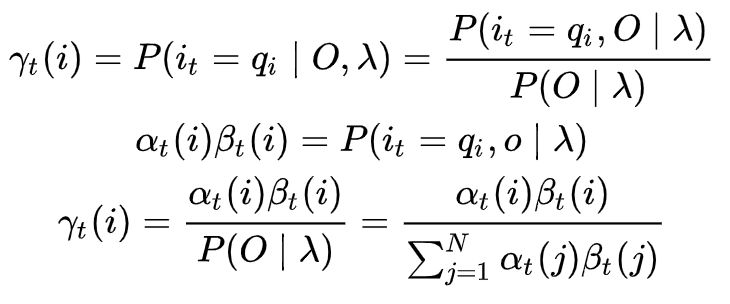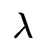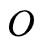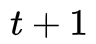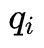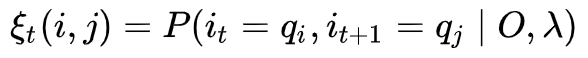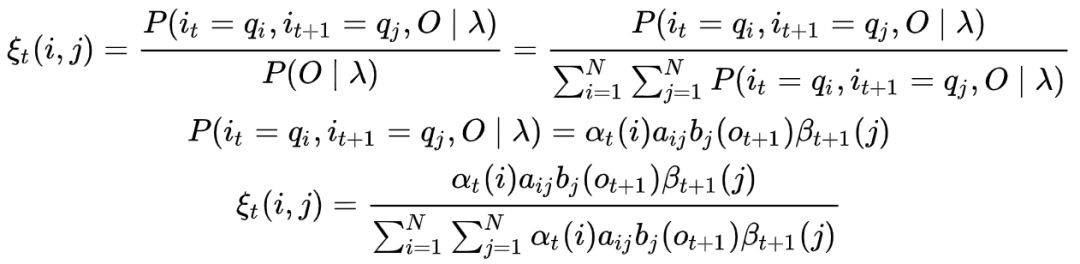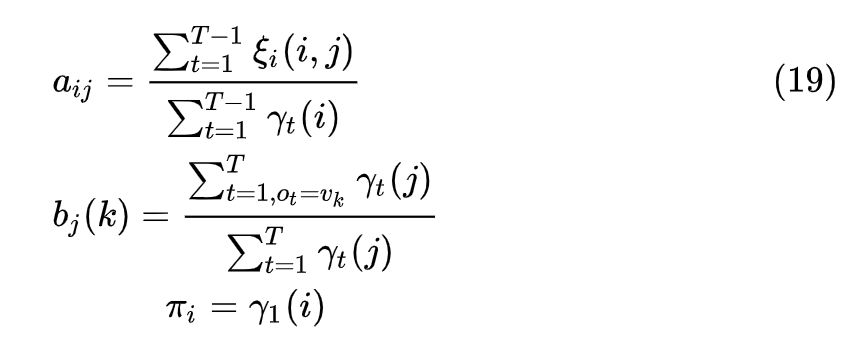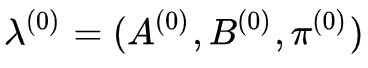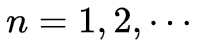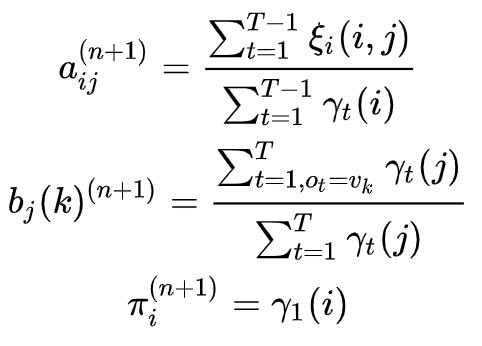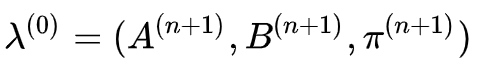赛尔笔记 | 隐马尔可夫模型

作者：哈工大SCIR硕士生 乐远

隐马尔可夫模型(HMM)是可用于标注问题的统计学习模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。

说到隐马尔可夫模型(HMM)，我们先来了解下马尔可夫模型(Markov模型)，Markov模型是一种统计模型，广泛地应用在语音识别，词性自动标注，音字转换，概率文法等各个自然语言处理的应用领域。

一. 马尔可夫模型(Markov模型)

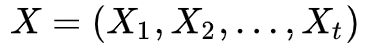
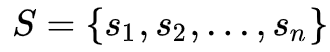
设是随机变量序列，其中每个随机变量的取值在有限集，称为状态空间。Markov特征是

• 有限历史假设

• 时间不变性
  

如果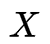 具有这些特征，那么这个随机变量序列称为一个马尔可夫过程（链）。

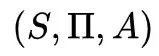
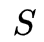
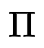
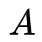
Markov的形式化表示：一个马尔可夫模型是一个三元组 ，其中 是状态的集合，是初始状态的概率，是状态间的转移概率。具体例子用图形表示如下，

相应的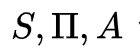分别是，

隐马尔可夫模型与马尔可夫模型不同的是各个状态（或者状态转移弧）都有一个输出，但是状态是不可见的。

最简单的情形：不同的状态只能有不同的输出，

增加一点灵活性：不同的状态，可以输出相同的输出，

再增加一点灵活性：输出在状态转移中进行，

最大的灵活性：在状态转移中以特定的概率分布输出，

这就得到了我们要讲的隐马尔可夫模型。

二. 隐马尔可夫模型(HMM)

1.HMM的形式化定义

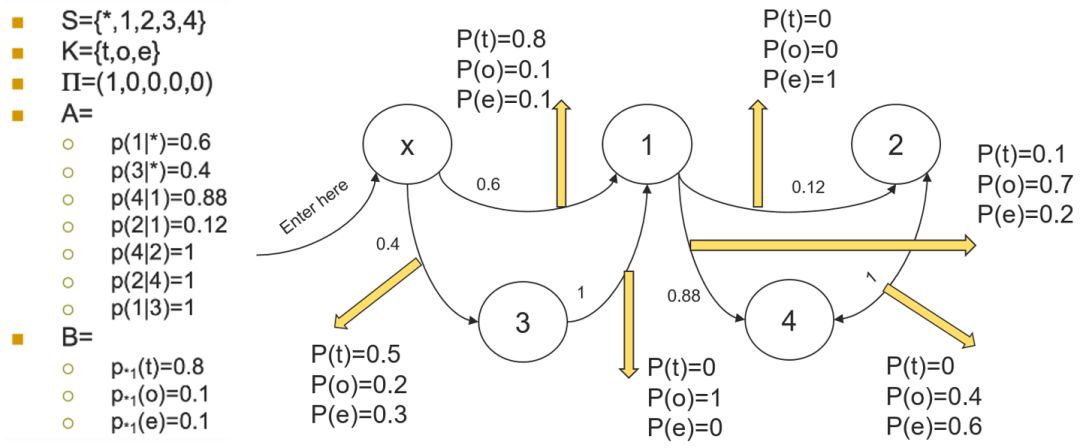
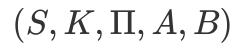
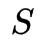
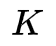
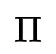
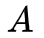
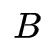
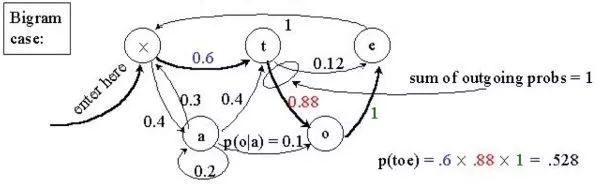
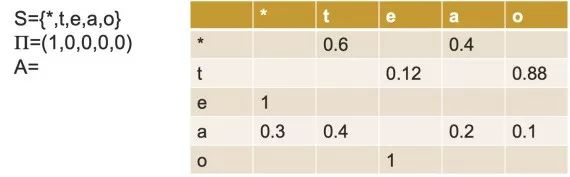
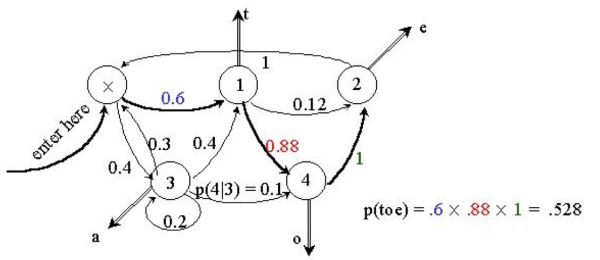
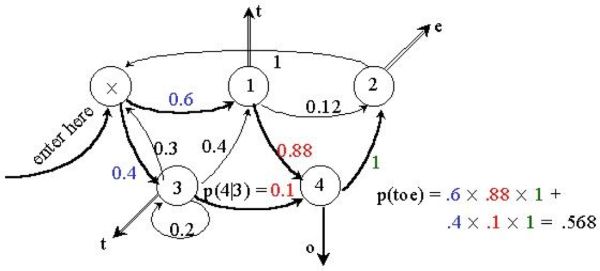
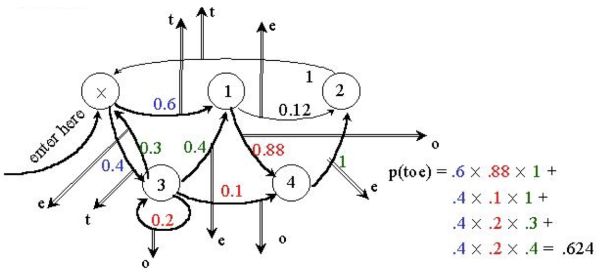
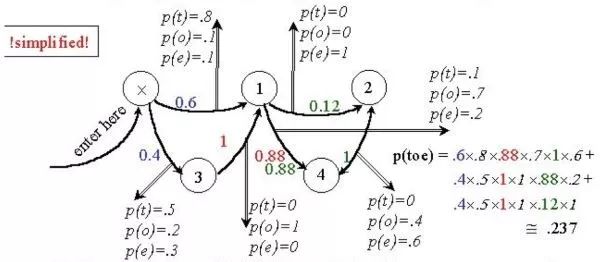
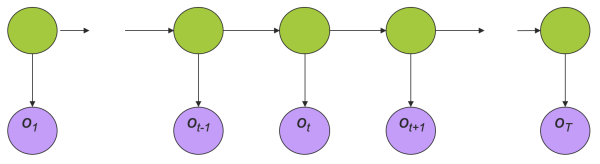
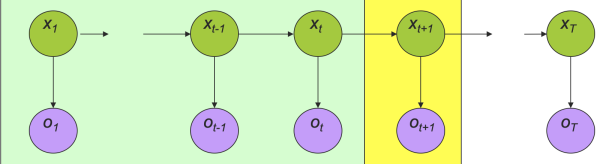
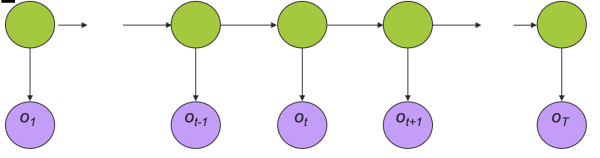
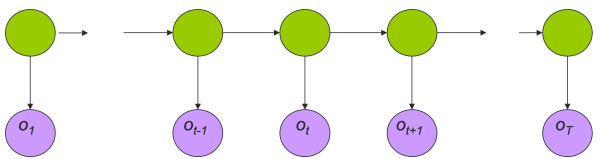
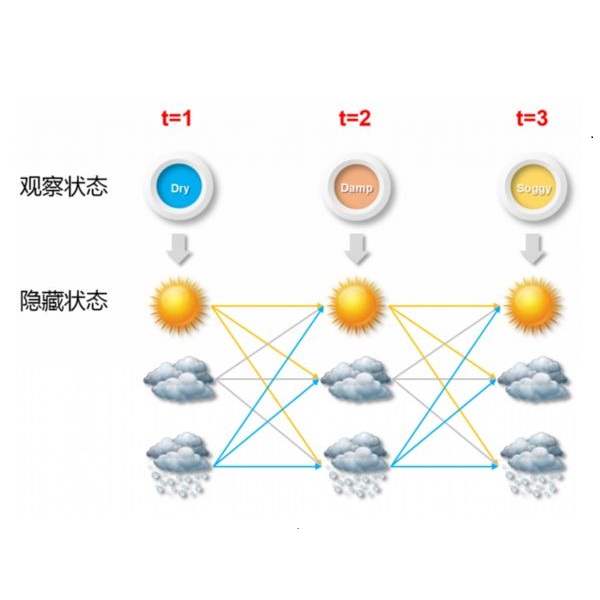
HMM是一个五元组，其中是状态的集合，是输出字符的集合，是初始状态的概率，是状态转移的概率,  是状态转移时输出字符的概率。

一个HMM的例子用图形表示如下，

2. 隐马尔可夫模型的三个基本问题

• 评估问题：给定一个模型 ，如何高效地计算某一输出字符序列的概率？

• 解码问题：给定一个输出字符序列，和一个模型，如何确定产生这一序列概率最大的状态序列？

• 学习问题：给定一个输出字符的序列，如何调整模型的参数使得产生这一序列的概率最大?

3. 评估问题的解法

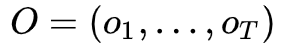
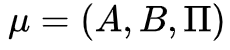
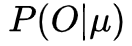
已知，，计算？

我们先来化简一下，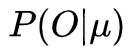

• 方案一：直接计算法

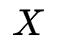
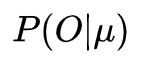
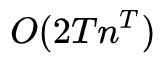
穷举所有可能的的情况，求和得到，但是时间复杂度太高，为。

• 方案二：前向算法(Forward algorithm)

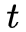
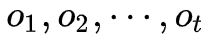
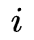
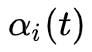
使用动态规划使得算法更高效，定义一个前向变量表示到时刻部分观测序列为且状态为的概率为向前概率，记为，即

则可以递推得到，

前向过程算法如下，

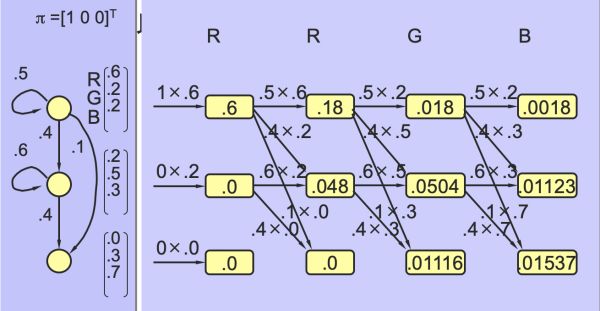
一个简单的前向过程例子如下，

• 方案三：向后算法(backward algorithm)

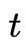
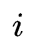
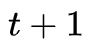
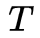
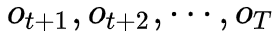
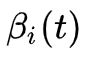
同样的道理，我们定义在时刻状态为的条件下，从到的部分观测序列为的概率为后向概率，记作，即

直接采用递推即可得到后向算法。

后向算法过程如下,

• 1. 初始化

• 2. 推导

• 3. 总和

4. 解码问题的解法

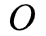
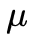
给定一个输出字符序列，和一个模型，如何确定产生这一序列概率最大的状态序列？

即

我们定义表示为在时刻到达状态，输出字符时，输出前面个字符的最可能路径的概率，

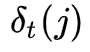
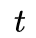
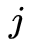
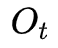
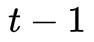
则有

这样我们就得到了维特比算法(Viterbi Algorithm)，算法过程如下：

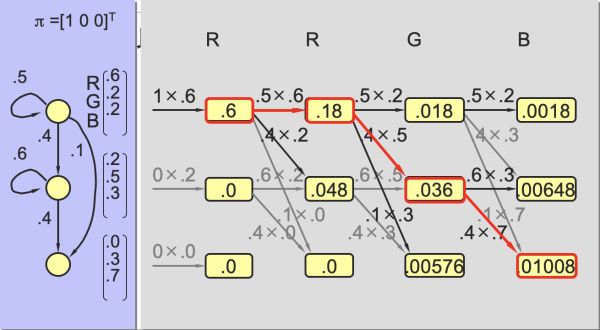
一个简单的viterbi算法举例如下，

5.  学习问题解法

给定一个输出字符的序列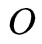，如何调整模型的参数使得产生这一序列的概率最大?

隐马尔可夫模型的学习，根据训练数据是包括观测数据和对应的状态序列还是只有观测序列，可以分为有监督学习和无监督学习，其中无监督的学习即是利用EM算法思想的Baum-Welch算法。

• 方案一：有监督学习

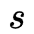
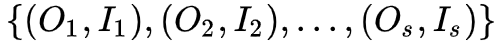
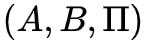
假设训练数据包含个长度相同的观测序列和对应的状态序列，那么可以利用极大似然估计法来估计隐马尔可夫模型的参数，具体估计方法如下：

• 1. 转移概率的估计

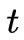
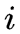
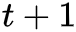
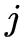
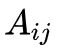
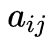
设样本中时刻处于状态时刻处于状态的频数为，那么状态转移概率的估计是

• 2. 观测概率的估计

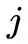
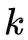
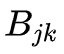
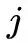
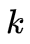
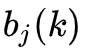
设样本中状态为并观测为的频数是，那么状态为观测为的概率的估计是

• 3. 初始状态概率的估计为个样本中初始状态为的概率

由于监督学习的方法需要使用训练数据，而人工标注的代价往往很高，有时会采用非监督学习的方法。

• 方案二：无监督学习——Baum-Welch算法

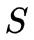
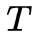
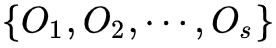
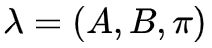
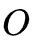
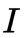
假设给定的训练数据只包含个长度为的观测序列而没有对应的状态序列，目标是学习隐马尔可夫模型的参数。我们将观测序列数据看做观测数据，状态序列数据看做不可观测数据，那么隐马尔可夫模型事实上是一个包含隐变量的概率模型

它的参数学习可以由EM算法实现。

（算法推导过程）

(1) 确定完全数据的对数似然函数 所有观测数据写成，所有的隐数据写成，完全数据是。完全数据的对数似然函数是。

(2) EM算法的E步：求函数的。

其中是隐马尔可夫模型参数的当前估计值，是要极大化的隐马尔可夫模型参数。因为，

所以函数可以拆分写成

式中求和都是对所有训练数据的序列总长度进行的。

(3) EM算法的M步：极大化函数，求模型参数。

由于要极大化的参数在函数式子中单独的出现在三个项中，所以只需要对各项分别极大化。第一项可以写成，

注意到满足，利用拉格朗日乘子法，写出拉格朗日函数

对其求导数并令结果为0，

得到

对求和得到,

再代入上式子得到，

第二项可以写成

类似于第一项，利用具有约束条件的拉格朗日乘子法恶意求出

第三项可以写成，

同样利用拉格朗日乘子法，约束条件是，注意只有在时对的偏导数才不为0，以表示，得到，

-----

为了简便，我们使用一下式子简化， 给定模型和观测，在时刻处于状态的概率记

有如下公式：

给定模型和观测，在时刻处于状态的概率记 :

有如下推倒：

我们结合上文以及EM算法可以推导如下公式

Baum-Welch算法过程：

输入：观测数据；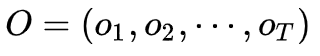

输出：隐马尔可夫模型参数。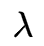

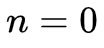
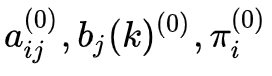
1. 初始化。对，选取得到模型

2. 递推。对

3. 终止。得到模型参数

---

参考资料

[1]公式参考李航《统计学习方法》

[2]图片选自哈尔滨工业大学关毅教授《自然语言处理》课程PPT

本期责任编辑：丁    效

本期编辑：刘元兴

---

欢迎加入NLP入门学习交流群

进群请添加AINLP小助手微信 AINLPer（id: ainlper)，备注NLP入门学习

推荐阅读

这个NLP工具，玩得根本停不下来

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

完结撒花！李宏毅老师深度学习与人类语言处理课程视频及课件（附下载）

从数据到模型，你可能需要1篇详实的pytorch踩坑指南

如何让Bert在finetune小数据集时更“稳”一点

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。

阅读至此了，分享、点赞、在看三选一吧🙏