用R语言实现密度聚类dbscan

会员服务 ·

用R语言实现密度聚类dbscan

2019 年 1 月 28 日 R语言中文社区

作者：张丹，R语言中文社区专栏特邀作者，《R的极客理想》系列图书作者，民生银行大数据中心数据分析师，前况客创始人兼CTO。
个人博客 http://fens.me， Alexa全球排名70k。

前言

聚类是一种将数据点按一定规则分群的机器学习技术，k-Means聚类是被用的最广泛的也最容易理解的一种。除了K-Means的方法，其实还有很多种不同的聚类方法，本文将给大家介绍基于密度的聚类，我们可以通过使用dbscan包来实现。

一、DBSCAN基于密度的聚类

二、dbscan包介绍

三、kNN()函数使用

四、dbscan()函数使用

五、hdbscan()函数使用

一、DBSCAN基于密度的聚类

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）聚类算法，它是一种基于高密度连通区域的基于密度的聚类算法，能够将具有足够高密度的区域划分为簇，并在具有噪声的数据中发现任意形状的簇。

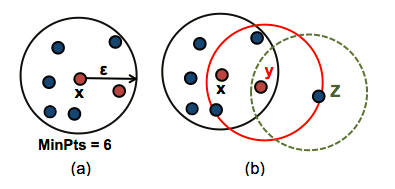
DBSCAN需要两个重要参数：epsilon(eps)和最小点(minPts)。参数eps定义了点x附近的邻域半径ε，它被称为x的最邻居。参数minPts是eps半径内的最小邻居数。

上图中(a)，数据集中的任何点x邻居(6=minPts)都被标记为核心点，ε是半径。上图中(b)，x为核心点，y的邻居小于(4<minpts)是边界点，但它属于核心点x的最邻居。z点既不是核心也不是边界点，它被称为噪声点或异常值。

dbscan算法将数据点分为三类：

核心点：在半径eps内含有超过minPts数目的点。
边界点：在半径eps内点的数量小于使用DBSCAN进行聚类的时候，不需要预先指定簇的个数，最终的簇的个数不确定。minPts,但是落在核心点的邻域内的点。
噪音点：既不是核心点也不是边界点的点

DBSCAN算法的执行过程

1、DBSCAN算法随机从一个未被访问的数据点x开始，以eps为半径搜索范围内的所有邻域点。

2、如果x点在该邻域内有足够数量的点，数量大于等于minPts，则聚类过程开始，并且当前数据点成为新簇中的第一个核心点。否则，该点将被标记为噪声。该点都会被标记为“已访问”。

3、新簇中的每个核心点x，它的eps距离邻域内的点会归为同簇。eps邻域内的所有点都属于同一个簇，然后对才添加到簇中的所有新点重复上述过程。

4、重复步骤2和3两个过程，直到确定了簇中的所有点才停止，即访问和标记了聚类的eps邻域内的所有点。

5、当完成了这个簇的划分，就开始处理新的未访问的点，发现新的簇或者是噪声。重复上述过程，直到所有点被标记为已访问才停止。这样就完成了，对所有点的聚类过程。

优点和缺点

DBSCAN具有很多优点，提前不需要确定簇的数量。不同于Mean-shift算法，当数据点非常不同时，会将它们单纯地引入簇中，DBSCAN能将异常值识别为噪声。另外，它能够很好地找到任意大小和任意形状的簇。

DBSCAN算法的主要缺点是，当数据簇密度不均匀时，它的效果不如其他算法好。这是因为当密度变化时，用于识别邻近点的距离阈值ε和minPoints的设置将随着簇而变化。在处理高维数据时也会出现这种缺点，因为难以估计距离阈值eps。

二、dbscan包介绍

dbscan包，提供了基于密度的有噪声聚类算法的快速实现，包括 DBSCAN（基于密度的具有噪声的应用的空间聚类），OPTICS（用于识别聚类结构的排序点），HDBSCAN（分层DBSCAN）和LOF（局部异常因子）算法，dbscan底层使用C++编程，并建立kd树的数据结构进行更快的K最近邻搜索，从而实现加速。

本文的系统环境为：

Win10 64bit
R 3.4.2 x86_64

dbscan包的安装非常简单，只需要一条命令就能完成。

1~ R
2> install.packages("dbscan")
3> library(dbscan)

函数列表：

dbscan(), 实现DBSCAN算法
optics(), 实现OPTICS算法
hdbscan(), 实现带层次DBSCAN算法
sNNclust(), 实现共享聚类算法
jpclust(), Jarvis-Patrick聚类算法
lof(), 局部异常因子得分算法
extractFOSC(),集群优选框架，可以通过参数化来执行聚类。
frNN(), 找到固定半径最近的邻居
kNN(), 最近邻算法，找到最近的k个邻居
sNN(), 找到最近的共享邻居数量
pointdensity(), 计算每个数据点的局部密度
kNNdist()，计算最近的k个邻居的距离
kNNdistplot()，画图，最近距离
hullplot(), 画图，集群的凸壳

dbscan包，提供了多个好用的函数，我们接下来先介绍3个函数，分别是kNN()，dbscan(), hdbscan()，其他的函数等以后有时间，再单独进行使用介绍。

三、kNN()函数使用

kNN()函数，使用kd-tree数据结构，用来快速查找数据集中的所有k个最近邻居。

函数定义：

1kNN(x, k, sort = TRUE, search = "kdtree", bucketSize = 10, splitRule = "suggest", approx = 0)

参数列表

x，数据矩阵，dist对象或kNN对象。
k，要查找的邻居数量。
sort，按距离对邻居进行排序。
search，最近邻搜索策略，使用kdtree，linear或dist三选一，默认为kdtree。
bucketSize，kd-tree叶子节点的最大值。
splitRule，kd-tree的拆分规则，默认用SUGGEST。
approx，使用近似方法，加速计算。

函数使用：以iris鸢尾花的数据集，做为样本。聚类是不需要有事前有定义的，所以我们把iris的种属列去掉。

 1# 去掉种属列
 2> iris2 <- iris[, -5]
 3> head(iris2)
 4  Sepal.Length Sepal.Width Petal.Length Petal.Width
 51          5.1         3.5          1.4         0.2
 62          4.9         3.0          1.4         0.2
 73          4.7         3.2          1.3         0.2
 84          4.6         3.1          1.5         0.2
 95          5.0         3.6          1.4         0.2
106          5.4         3.9          1.7         0.4

使用kNN()函数，来计算iris2数据集中，每个值最近的5个点。

 1# 查询最近邻的5个点
 2> nn <- kNN(iris2, k=5)
 3
 4# 打印nn对象
 5> nn
 6k-nearest neighbors for 150 objects (k=5).
 7Available fields: dist, id, k, sort
 8
 9# 查询nn的属性列表
10> attributes(nn)
11$names
12[1] "dist" "id"   "k"    "sort"
13
14$class
15[1] "kNN" "NN"

打印出，每个点最近邻的5个点。行，为每个点索引值，列，为最近邻的5个点，输出的矩阵为索引值。

1> head(nn$id)
2      1  2  3  4  5
3[1,] 18  5 40 28 29
4[2,] 35 46 13 10 26
5[3,] 48  4  7 13 46
6[4,] 48 30 31  3 46
7[5,] 38  1 18 41  8
8[6,] 19 11 49 45 20

打印出，每个点与最近的5个点的距离值。行，为每个点的索引，列，为最近邻的5个点，输出的矩阵为距离值。

1> head(nn$dist)
2             1         2         3         4         5
3[1,] 0.1000000 0.1414214 0.1414214 0.1414214 0.1414214
4[2,] 0.1414214 0.1414214 0.1414214 0.1732051 0.2236068
5[3,] 0.1414214 0.2449490 0.2645751 0.2645751 0.2645751
6[4,] 0.1414214 0.1732051 0.2236068 0.2449490 0.2645751
7[5,] 0.1414214 0.1414214 0.1732051 0.1732051 0.2236068
8[6,] 0.3316625 0.3464102 0.3605551 0.3741657 0.3872983

如果我们要查看索引为33的点，与哪5个点最紧邻，可以用下面的方法。

 1# 设置索引
 2> idx<-33
 3
 4# 打印与33，最近邻的5个点的索引
 5> nn$id[idx,]
 6 1  2  3  4  5 
 734 47 20 49 11 
 8
 9# 画图
10> cols = ifelse(1:nrow(iris2) %in% nn$id[idx,],"red", "black")
11> cols[idx]<-'blue'
12> plot(iris2,pch = 19, col = cols)

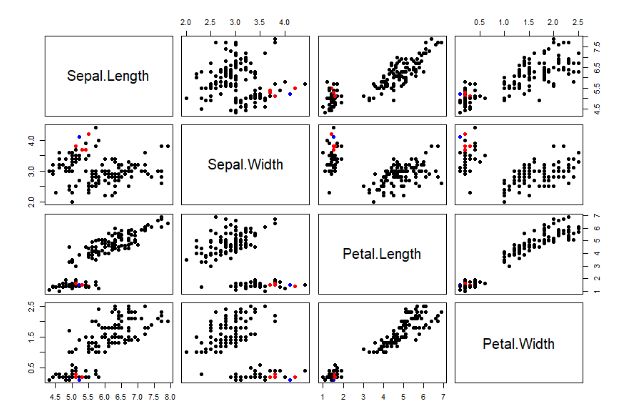
我们的数据集是多列的，把每2列组合形成的二维平面，都进行输出。蓝色表示索引为33的点，红色表示最紧邻的5个点，黑色表示其他的点。

从图中，可以很直观的看到，这几点确实是密集的在一起，也就是找到了最近邻。

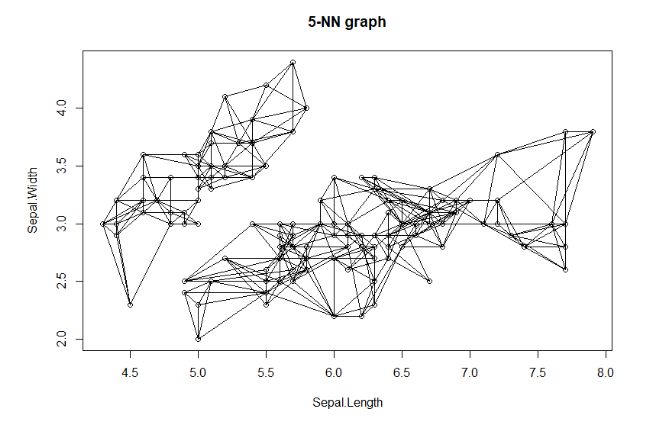
接下来，我们画出连线图，选取第一列(Sepal.Length)和第二列(Sepal.Width)，按取画出最紧邻前5连接路径。

1> plot(nn, iris2)

通过连接路径，我们就能很清晰的看到，最紧邻算法的分组过程，连接在一起的就够成了一个分组，没有连接在一起的就是另外的分组，上图中可以看出来分成了2个组。

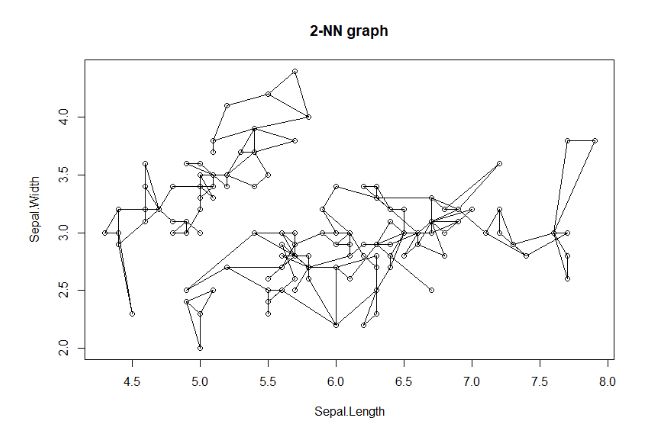
再对nn进行二次最近邻计算，画出前2的连接路径。

1> plot(kNN(nn, k = 2), iris2)

四、dbscan()函数使用

dbscan是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。同一类别的样本，他们之间的紧密相连的，也就是说，在该类别任意样本周围不远处一定有同类别的样本存在。

函数定义：

1dbscan(x, eps, minPts = 5, weights = NULL, borderPoints = TRUE, ...)

参数解释：

x，矩阵或者距离对象，frNN对象。
eps，半径的大小。
minPts，半径区域中的最小点数量，默认为5
weights，数据点的权重，仅用于加权聚类
borderPoints，边界点是否为噪声，默认为TRUE；为FALSE时，边界点为噪声。
…，将附加参数传递给固定半径最近邻搜索算法，调用frNN。

函数使用：以iris鸢尾花的数据集，做为样本。聚类是不需要有事前有定义的，所以我们把iris的种属列去掉。

 1# 去掉种属列
 2> iris2 <- iris[, -5]
 3> head(iris2)
 4  Sepal.Length Sepal.Width Petal.Length Petal.Width
 51          5.1         3.5          1.4         0.2
 62          4.9         3.0          1.4         0.2
 73          4.7         3.2          1.3         0.2
 84          4.6         3.1          1.5         0.2
 95          5.0         3.6          1.4         0.2
106          5.4         3.9          1.7         0.4

在使用dbscan函数时，我们要输出2个参数，eps和minPts。

eps，值可以使用绘制k-距离曲线(k-distance graph)方法得到，在k-距离曲线图明显拐点位置为较好的参数。若参数设置过小，大部分数据不能聚类；若参数设置过大，多个簇和大部分对象会归并到同一个簇中。
minPts，通常让minPts≥dim+1，其中dim表示数据集聚类数据的维度。若该值选取过小，则稀疏簇中结果由于密度小于minPts，从而被认为是边界点儿不被用于在类的进一步扩展；若该值过大，则密度较大的两个邻近簇可能被合并为同一簇。

下面我们通过绘制k-距离曲线，寻找knee，即明显拐点位置为对应较好的参数，找到适合的eps值。使用kNNdistplot()函数，让参数k=dim + 1，dim为数据集列的个数，iris2是4列，那么设置k=5。

1# 画出最近距离图
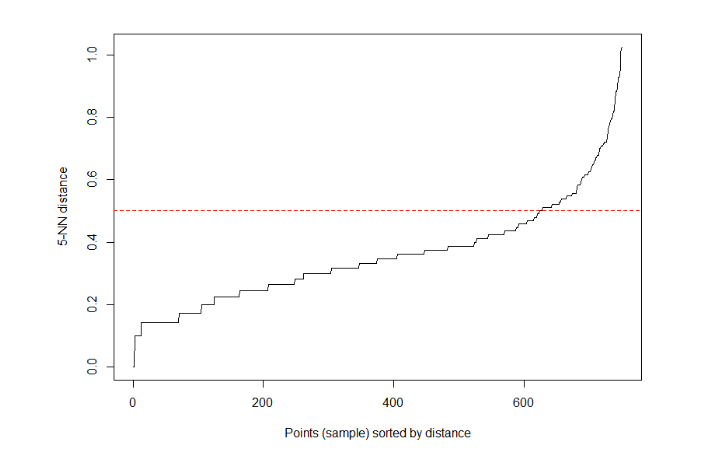
2> kNNdistplot(iris2, k = 5)
3> abline(h=0.5, col = "red", lty=2)

kNNdistplot()会计算点矩阵中的k=5的最近邻的距离，然后按距离从小到大排序后，以图形进行展示。x轴为距离的序号，y轴为距离的值。图中黑色的线，从左到右y值越来越大。

通过人眼识别，k-距离曲线上有明显拐点，我们以y=0.5平行于x轴画一条红色线，突出标识。所以，最后确认的eps为0.5。

调用dbscan()函数，进行对iris2数据集进行聚类，eps=0.5，minPts=5。

 1> res <- dbscan(iris2, eps = 0.5, minPts = 5)
 2> res
 3DBSCAN clustering for 150 objects.
 4Parameters: eps = 0.5, minPts = 5
 5The clustering contains 2 cluster(s) and 17 noise points.
 6
 7 0  1  2 
 817 49 84 
 9
10Available fields: cluster, eps, minPts

聚类后，一共分成了2组，第1组49个值，第2组84个值，另外，第0组17个值为噪声点。把聚类的结果画图展示。

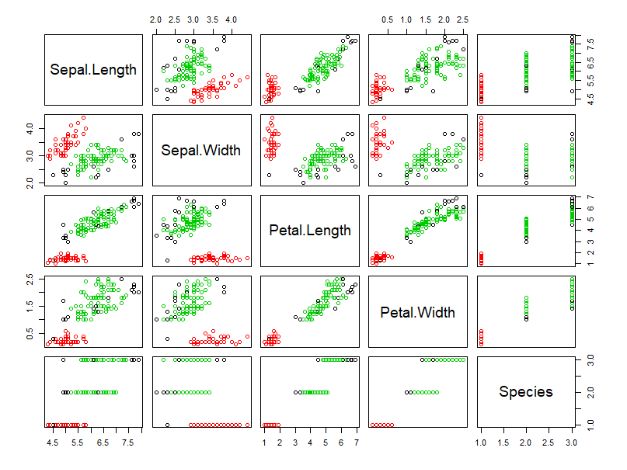
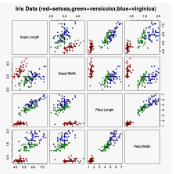
1> pairs(iris, col = res$cluster + 1L)

数据集是多列的，把每2列组合形成的二维平面，都进行输出。红色点表示第1组，绿色点表示为第2组，黑色点表示噪声点。这样就完成了有噪声的基于密度的dbscan聚类。

五、hdbscan()函数使用

hdbscan()，快速实现了分层DBSCAN算法，与stats包中的hclust()方法形成的传统分层聚类方法类似。

函数定义：

1hdbscan(x, minPts, xdist = NULL,gen_hdbscan_tree = FALSE, gen_simplified_tree = FALSE)

参数解释：

x，矩阵或者距离对象
minPts，区域中的最小点数量
xdist，dist对象，可以提前算出来，当参数传入
gen_hdbscan_tree，生成一个hdbscan树
gen_simplified_tree，生成一个简化的树结构

3.1 iris鸢尾花的数据集
以iris鸢尾花的数据集，做为样本，去掉种属列。设置minPts =5让当前群集中最小的数量为5，开始聚类。

1> hcl<-hdbscan(iris2, minPts = 5);hcl
2HDBSCAN clustering for 150 objects.
3Parameters: minPts = 5
4The clustering contains 2 cluster(s) and 0 noise points.
5
6  1   2 
7100  50 
8
9Available fields: cluster, minPts, cluster_scores, membership_prob, outlier_scores, hc

聚类后，一共分成了2组，第1组100个值，第2组50个值，没有噪声点。生成的hcl对象包括6个属性。
属性解释

cluster，表明属性哪个群集，零表示噪声点。
minPts，群集中最小的数量
cluster_scores，每个突出（“平坦”）群集的稳定性分数之和。
membership_prob，群集内某点的“概率”或个体稳定性
outlier_scores，每个点的异常值
hc，层次结构对象

把聚类的结果画图展示。

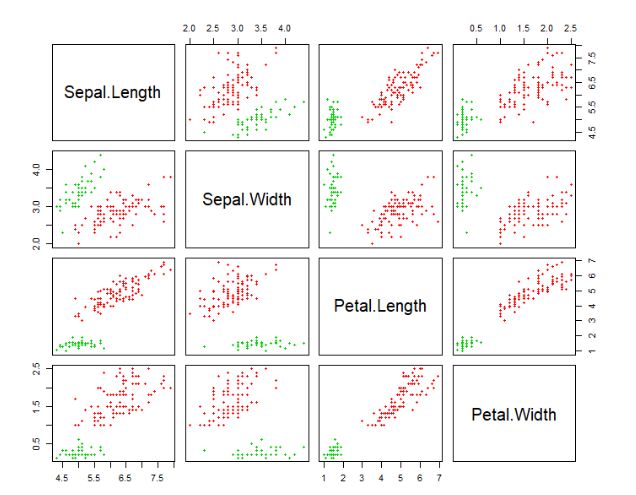
1> plot(iris2, col=hcl$cluster+1, pch=20)

数据集是多列的，把每2列组合形成的二维平面，都进行输出。红色点表示第1组，绿色点表示为第2组，这样就完成了hdbscan聚类。

打印hcl对象层次结构，包括150个数据，聚法方法是健壮单一的，距离是相互可达。

1> hcl$hc
2
3Call:
4hdbscan(x = iris2, minPts = 5)
5
6Cluster method   : robust single 
7Distance         : mutual reachability 
8Number of objects: 150

画出层次的合并过程图

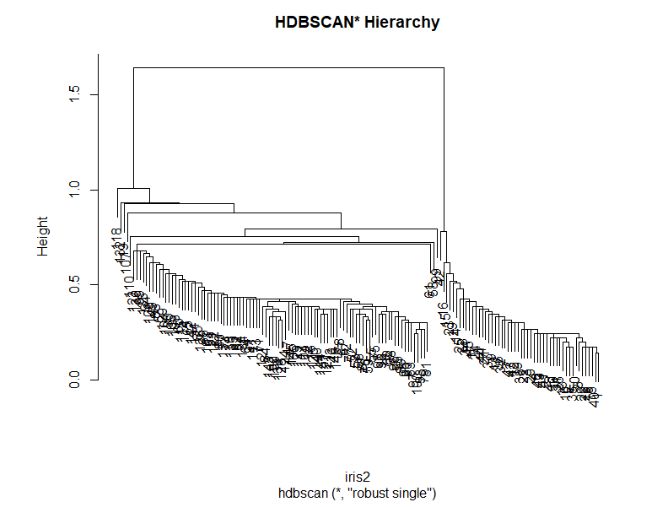
1> plot(hcl$hc, main="HDBSCAN* Hierarchy")

从图可以清楚的看出，主要的2类的分支，区分度比较高。

3.2 moons数据集
由于iris数据集用hdbscan聚类获得的结果，与真实的数据分类结果不一致。我们再用dbscan包自带的数据集moons做一下测试。

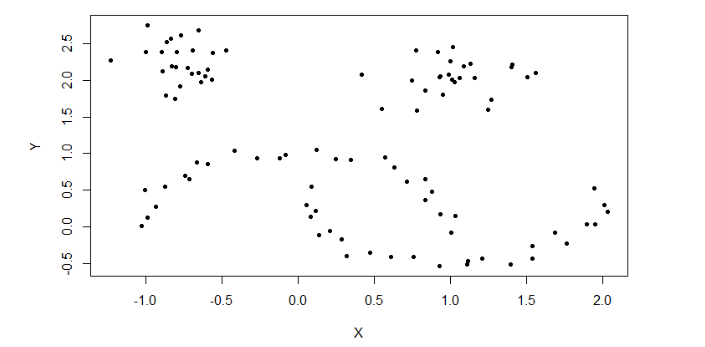
先准备数据，加载moons数据集，了解数据基本情况，画出散点图。

 1# 加载dbscan自带数据集
 2> data("moons")
 3> head(moons)
 4            X          Y
 51 -0.41520756  1.0357347
 62  0.05878098  0.3043343
 73  1.10937860 -0.5097378
 84  1.54094828 -0.4275496
 95  0.92909498 -0.5323878
106 -0.86932470  0.5471548
11
12# 画出散点图
13> plot(moons, pch=20)

用hdbscan()函数，实现层次dbscan算法。

 1> cl <- hdbscan(moons, minPts = 5)
 2> cl
 3HDBSCAN clustering for 100 objects.
 4Parameters: minPts = 5
 5The clustering contains 3 cluster(s) and 0 noise points.
 6
 7 1  2  3 
 825 25 50 
 9
10Available fields: cluster, minPts, cluster_scores, membership_prob, outlier_scores, hc

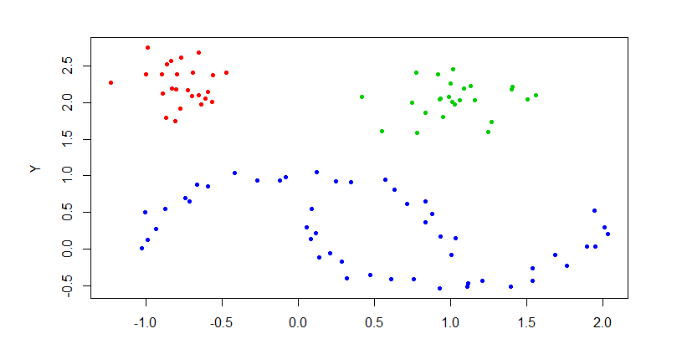
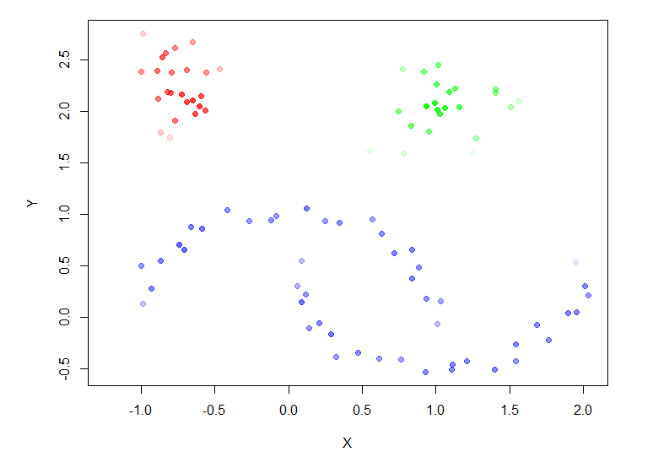
一共100条数据，被分成了3类，没有噪声。把聚类的结果画图展示。

1# 画图
2> plot(moons, col=cl$cluster+1, pch=20)

打印层次结构

1> cl$hc
2Call:
3hdbscan(x = moons, minPts = 5)
4
5Cluster method   : robust single 
6Distance         : mutual reachability 
7Number of objects: 100

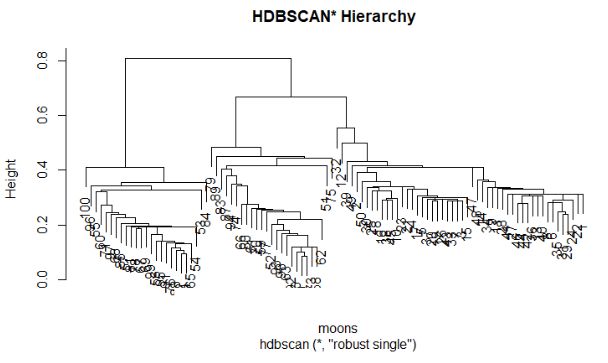
画出层次的合并过程图

1> plot(cl$hc, main="HDBSCAN* Hierarchy")

从图可以清楚的看出，主要的3类的分支，区分度比较高。

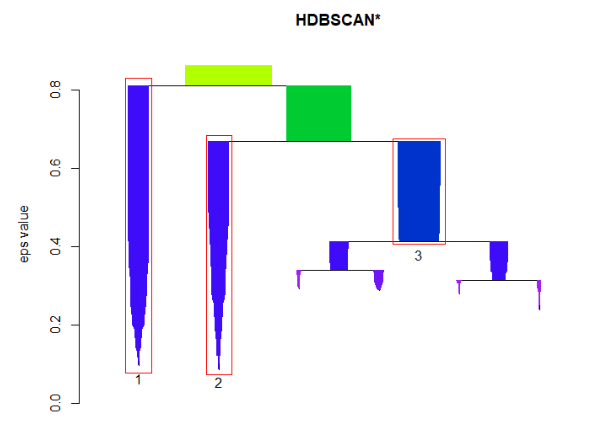
如果我们想省略分层的细节，我们可以只画出主要分支，并标识类别。

1plot(cl, gradient = c("purple", "blue", "green", "yellow"), show_flat = T)

接下来，我们要对群集的稳定性做一些优化，cluster_scores属性可以查看集群的得分。

1> cl$cluster_scores
2        1         2         3 
3110.70613  90.86559  45.62762

通过membership_prob属性，画图表示个体的稳定性。

 1# 打印membership_prob
 2> head(cl$membership_prob)
 3[1] 0.4354753 0.2893287 0.4778663 0.4035933 0.4574012 0.4904582
 4
 5# 计算群集的数量
 6> num<-length(cl$cluster_scores)
 7
 8# 从彩虹色中取得对应数量的颜色
 9> rains<-rainbow(num)
10> cols<-cl$cluster
11> cols[which(cols==1)]<-rains[1]
12> cols[which(cols==2)]<-rains[2]
13> cols[which(cols==3)]<-rains[3]
14
15# 设置透明度，表示个体的稳定性
16> plot(moons, col=alpha(cols,cl$membership_prob), pch=19)

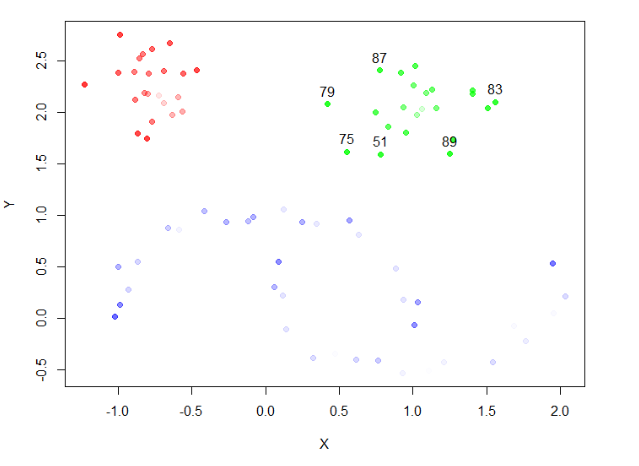
最后，我们可以在图中，在标记出异常值得分最高的前6个点。

1# 对异常值进行排序，取得分最高的
2> top_outliers <- order(cl$outlier_scores, decreasing = TRUE) %>% head
3> plot(moons, col=alpha(cols,cl$outlier_scores), pch=19)
4> text(moons[top_outliers, ], labels = top_outliers, pos=3)

从图中看到，异常得分高的点(outlier_scores)与个体的稳定性(membership_prob)，并不是同一类点。异常值通常被认为是，偏离其假定的基础分布的离群点。

写

在最后

通过上面3个函数的使用案例，我们了解了如何用dbscan包实现基于密度的聚类方法。真实世界的数据是复杂的，我们用来分析数据的工具也是多样的，多掌握一种工具、多一些知识积累，让我们迎接真实世界数据的挑战吧。

往期精彩：

公众号后台回复关键字即可学习

回复爬虫            爬虫三大案例实战
回复 Python       1小时破冰入门
回复数据挖掘     R语言入门及数据挖掘
回复人工智能     三个月入门人工智能
回复数据分析师  数据分析师成长之路
回复机器学习     机器学习的商业应用
回复数据科学     数据科学实战
回复常用算法常用数据挖掘算法