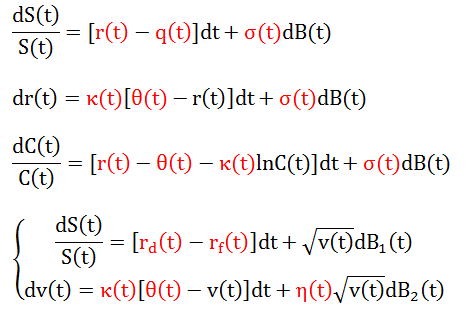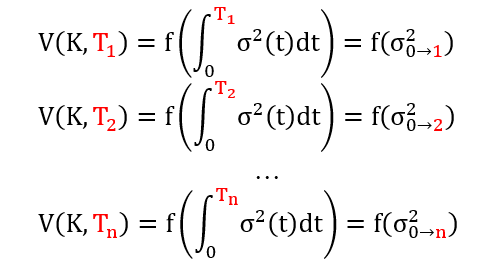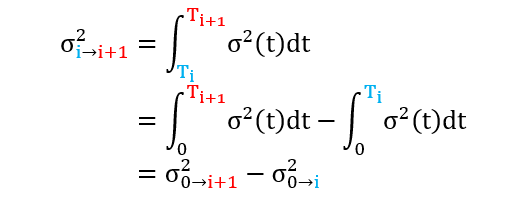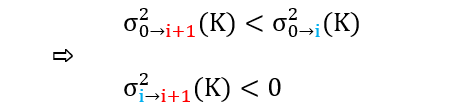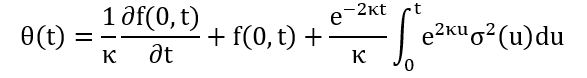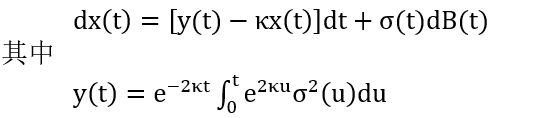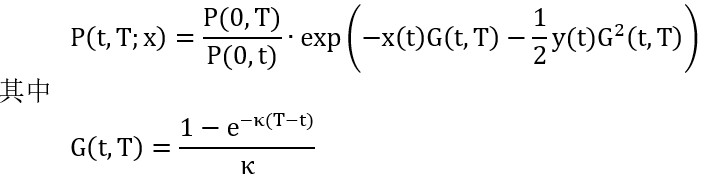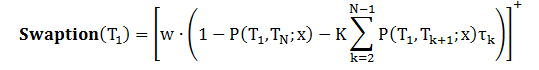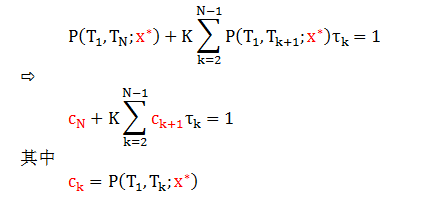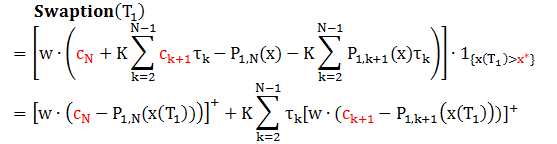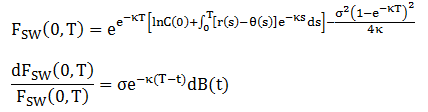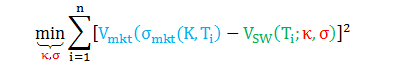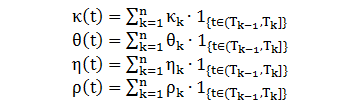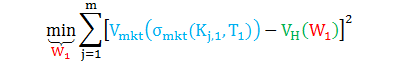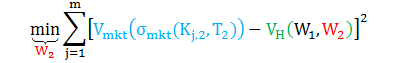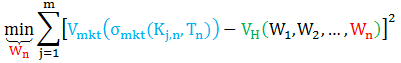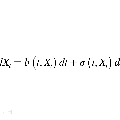模型校正

本文首发于量化投资和机器学习，倍感荣幸

引言

斯蒂文管理着一个交易组合，里面包含着各种资产类 (asset class) 的金融产品。

老板

屯有欧元，欧元对美元 (EURUSD) 可能会涨，3 个月后锁定一个汇率换成美元

斯蒂文

买 EURUSD 看涨期权 (call option)

老板

美元三个月同业拆放利率 (USD Libor 3M) 可能会降，1 年后锁定一个利率赚利差

斯蒂文

买 USD 利率下限 (IR floor)

老板

咖啡价格 3 个月可能会涨，抓住它的平均涨幅

斯蒂文

买咖啡亚式固定行权看涨期权 (Asian fixed strike call option)

老板

通用汽车 (GM) 股票在 1 年内可能会涨，但是一旦超过 38 就不会跌破 30

斯蒂文

买 GM 向上敲出障碍看跌期权 (up-and-out putoption)，障碍价位 38，行权价为 30

要买这么多金融衍生品，以什么价格买？这可不是简单的折现现金流 (discounted cash flow) 就可以算出来，都需要对其原生资产 (underlying asset) 价格进行建模。原因很简单，衍生品的价值是原生资产价格的函数。

• 外汇看涨期权的价值是汇率价格的函数

• 利率下限的价值是利率价格的函数

• 商品亚式期权的价值是商品价格的函数

• 股权障碍期权的价值是股票价格的函数

但是产品定价 (instrument pricing) 易，模型校正 (model calibration) 难，因为

• 定价是个正问题，给定模型参数算出产品价格

• 校正是个反问题，给定产品价格反推模型参数

 

为了让大家保持兴趣，现在来看看两个最简单的定价和校正：

1. 定价问题是 1 + 2 = 3，把加法看成是个“模型”，那么与之对应的校正问题就是 1 加上多少等于 3，校正 (用减法 3 - 1) 出来的结果是 2

2. 定价问题是 sin(π/6) = 0.5，把正弦函数看成是个“模型”，那么与之对应的校正问题就是 sin 多少等于 0.5，校正 (用反正弦 argsin(0.5)) 出来的结果是 π/6 

虽然上面两例“校正”不难，但也比“定价”难吧。在量化金融中，用复杂模型的定价问题已经不易，那么相对应的校正问题更加困难，如：

定价问题是 V(σ) = 1 美元，把 V 看成是个期权定价公式，那么与之对应的校正问题就是多大的波动率 σ 带入公式里得到期权价值 1 美元。

本帖就为大家展示各种资产类的常见模型的模型校正！里面画的图全是基于真实的市场数据，而作者也有一套系统的程序来实现各种模型校正。出于里面有些技巧是公司或客户的私有财产和作者多年以来的心血，作者还是不发整套代码怕担当法律责任，但是有问必答！

目录

第一章 - 前戏王

    1.1 模型参数形式

    1.2 随机微分方程

第二章 - 股权类

    2.1 Black-Scholes 模型

    2.2 市场标准产品和数据

    2.3 市场价格和模型价格

    2.4 模型校正

    2.5 校正结果

第三章 - 利率类

    3.1 Hull-White 模型

    3.2 市场标准产品和数据

    3.3 市场价格和模型价格

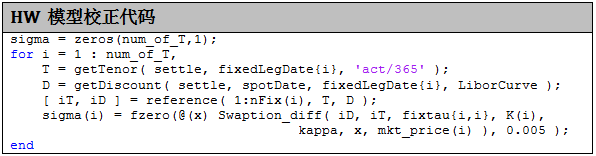
    3.4 模型校正 (cap)

    3.5 模型校正 (swaption)

    3.6 校正结果

第四章 - 商品类

    4.1 Schwartz 模型

    4.2 市场标准产品和数据

    4.3 市场价格和模型价格

    4.4 模型校正

    4.5 季节性调整

    4.6 Kalman Filter 方法

第五章 - 外汇类

    5.1 Heston 模型

    5.2 市场标准产品和数据

    5.3 市场价格和模型价格

    5.4 模型校正

    5.5 校正结果

总结

第一章 - 前戏王

1.1

模型参数类型

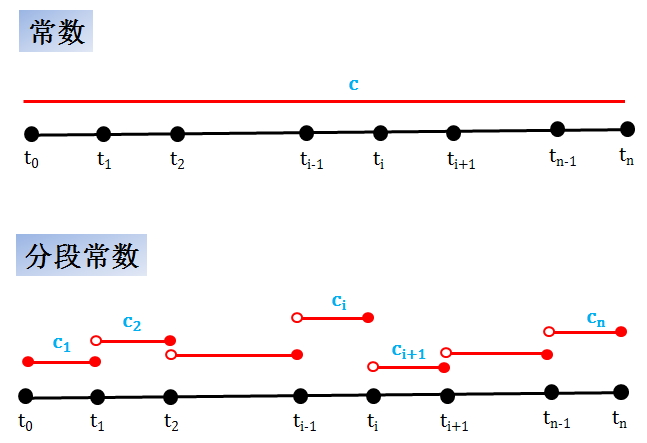
在金融模型中时间 t 是个重要变量，而模型参数 c 通常和 t 有关，写作c(t)。在建模时，将 c(t) 的整个函数形式完全描述出来不容易也不实际，通常把 c(t) 看成是常数形式和分段常数形式，如下图：

给定时间结构 t₀ < t₁ < … < t_i-1 < … < t_n，常数和分段常数的表达形式如下表所示

1.2

随机微分方程

随机微分方程 (SDE) 就是常微分方程 (ODE) 加个随机过程。在各种金融衍生品模型中，其对应的原生资产都能用 SDE 来描述。比如股票类 Black-Scholes 模型，利率类 Hull-White 模型，商品类 Schwartz 模型和外汇类 Heston 模型相对应的 SDE 如下：

不严谨来讲，我们可以把 SDE 当成模型，把红色项就是模型参数，这些参数都不是随意给定，而是从金融市场中“校正”出来的。

第二章 - 股权类

2.1

Black-Scholes 模型

模型介绍

股权类的 Black-Scholes (BS) 模型下的 SDE 是描述股票价格 (stock price) 的走势：               

Fischer Black 和 Myron Scholes 在 1973 年提出此模型，其论文题目是

The Pricing of Options and Corporate Liabilities

 

模型参数

一般情况下

• r(t) 和 q(t) 当成常数

• σ(t) 可以是常数，但通常是分段常数

它们的获取方式为

• r: 根据股票结算的货币，找到其掉期曲线，如美元对应 USD Libor 3M 曲线，欧元对应 EUR Euribor 6M 曲线等，在曲线上插出 T 点的 r 值

• q: 根据该股票在估值日和到期日 T 之间的所有离散红利，折现到 0 点得到红利现值 div，再利用公式 div = e^-qT 计算出 T 点的 q 值，q = -ln(div/T)

• σ 或 σ(t): 从一系列股权欧式期权中校正出来

2.2

市场标准产品和数据

产品定义

股权类市场标准产品是“一系列不同行权价格 K 和不同年限 T 股权欧式期权 (EQ option)”，定义如下：

在股权欧式期权 (equity vanilla option) 合约下，买卖方将同意以下内容：

• 买方付出期权金 (premium) 便有权利 (right) 去行使，而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务。

• 看涨期权：买方有权利在到期日以 K 买入 S，而卖方一旦被行使期权时，则有义务以 K 卖出 S

• 看跌期权：买方有权利在到期日以 K 卖出 S，而卖方一旦被行使期权时，则有义务以 K 买入 S

其中 S 是到期日股权的价格，K 是执行价格 (strike price)。

市场数据

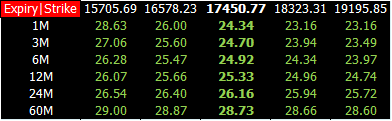
它们的成交价就是用于模型校正的市场数据，但市场惯例是用波动率当市场数据，原因是价格在价内 (ITM) 和价外 (OTM) 是差别会很大，而波动率是一个没有单位的量。某天的日经平均指数 (N225) 的真实数据如下：

上图数据又称 EQ option 波动率平面，它是二维数据结构

 

• 行对应的年限 (expiry)，期权年限从 1 个月到 5 年

• 列对应的行权价格 (strike)，注意第三列白色粗体 17450.77 是 ATM 行权价格，其对应的绿色粗体是 ATM 波动率

• 波动率与行权价格和年限有关，可写成 σ(K, T)

• 波动率单位是%，28.63 实际上指的是 28.63%

• 市场波动率带进 BS 公式得到期权的市场价格

2.3

市场价格和模型价格

市场价格

EQ option 市场价格是之后模型校正的基准 (benchmark)。关于 BS 模型的 EQ option 公式推导细节，可参考 Options, Futures and Other Derivatives, 9th edition, Chapter15, Appendix.

模型价格

当模型参数为 t 的函数时，关于 BS 模型的 EQ option 公式推导细节，可参考 Volatility and Correlation, 2nd edition, Chapter3.

2.4

模型校正

在 EQ option 市场上，对每个标准 K 有 n 个到期的 EQ option，到期日分别为

    

    0 = T₀ < T₁ < … < T_i < … < T_n 

而对于每个 T_i ，EQ option 的行权价格为 K₁, …, K_j, …, K_m。  

接下来我们分别讨论当模型参数为常数和分段常数是的校正过程。

 

常数型参数

当参数为常数时，BS 模型校正本质上是找到“最优” σ，从而最小化一系列 EQ option 的市场价格和模型价格之间的差异，其目标函数为：

分段常数型参数

 

当参数为分段常数时，对每个标准 K，市场上都有一系列 T_i 到期的 EQ option，由上面公式发现期权价格 V 是 σ²(t) 积分的函数，如下：

注意 σ_0-i 是从 0 到 T_i 的波动率 σ(t) 的均方根 (root-mean-square)，而它们可以直接反解 BS 公式得到。之后我们可以得到从 T_i 到 T_i+1

上面公式建立了即期方差到远期方差的关系，而这个关系通常称为方差平衡条件 (balance-of-variance condition)。具体步骤如下：

 

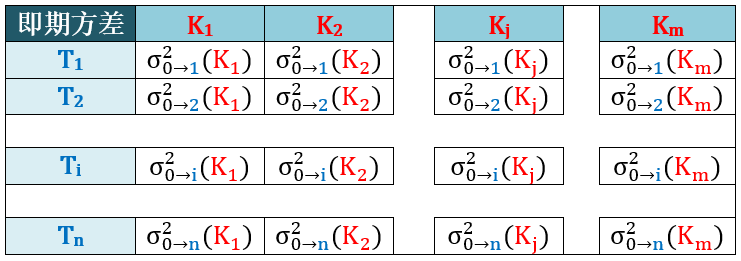
1. 在每个 K_j 下的所有年限 T 上计算：即期方差 = σ²_mkt ∙ T






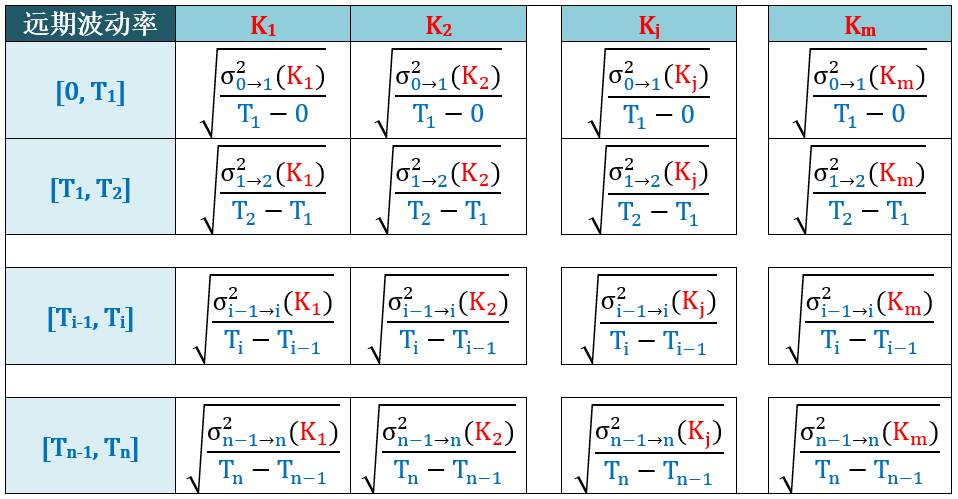
2. 用方差平衡条件从即期方差推出远期波动率，如下表所示

从即期方差推出远期波动率的代码如下：

在做模型校正的同时，一旦我们发现下面的关系，那么就有套利机会。

上式意思就是股票价格到 T_i+1 的不确定性比到 T_i 的不确定性还小，这显然违背常理。如果有这种机会出现，买 T_i+1 到期的便宜期权，卖 T_i 到期的昂贵期权。

2.5

校正结果

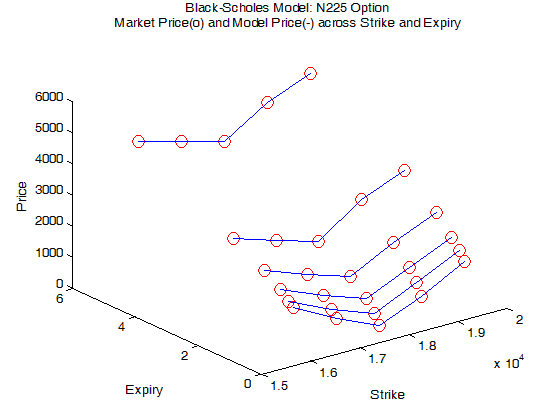
下图展示着 N225 option 的市场价格 (红圈) 和模型价格 (蓝线)，发现它们在不同 K 和 T 时都高度吻合。

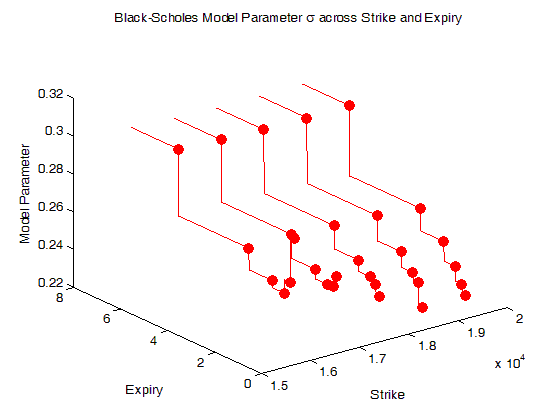
下图展示着在不同 K 下的分段常数 σ(t)，基本上 σ(t) 是 t 的增函数，走势正常。

第三章 - 利率类

3.1

Hull-White 模型

模型介绍

利率类的 Hull-White (HW) 模型下的 SDE 是描述短期利率 (short rate) 的走势：

John Hull 和 Alan White 在 1990 年提出此模型，其论文题目是

Pricing Interest-Rate Derivative Securities

 

模型参数

一般情况下

• κ(t) 当成常数

• σ(t) 可以是常数，但通常是分段常数

• θ(t) 是 t 的函数

 

它们的获取方式为

• κ: 根据历史数据人为设定，也可以从一系列利率期权中校正出来

• σ 或 σ(t): 从一系列利率期权中校正出来

 

• θ(t): 从收益率曲线中校正出来

    其中 f(0,t) 是 0 点看到 t 点瞬时远期利率

为了消除 θ(t) 这个复杂项，令 x(t) = r(t) – f(0,t)，那么 x(0) = r(0) – f(0,0) = 0。原来 r(t) 的 SDE 转换成 x(t) 的 SDE：

         

在 HW 模型下的零息债券 (zero-coupon bond, ZCB) 的公式如下：

 

关于上面 θ(t) 和 P(t,T) 推导细节，可以参考 Interest Rate Modeling – Volumn II,Term Structure Model, Chapter 10, 10.1.2.2

3.2

市场标准产品和数据

产品定义

 

利率类市场标准产品包括：

1. 一系列不同行权价格 K 和不同年限 T 利率上限 (cap)

2. 一系列不同行权价格 K，不同期权年限 T_O 和不同掉期年限 T_U 利率掉期期权 (swaption)

Cap 的定义如下：

在利率上限或下限 (interest rate cap/floor) 合约下，买卖方将同意以下内容：

 

• 买方付出期权金 (premium) 便有权利 (right) 去行使，而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务。

• 双方就未来某一时期商定一个固定利率 K 作为利率上限/下限

• 上限：买方有权利在每期获得市场利率 L 与上限利率 K 的差额 (L – K)，而卖方一旦被行使期权时，则有义务将市场利率 L 与上限利率 K 的差额支付给买方

• 下限：买方有权利在每期获得下限利率 K 和市场利率 L 的差额 (K – L)，而卖方一旦被行使期权时，则有义务将下限利率 K 和市场利率 L 的差额支付给买方

其中 L 通常是 LIBOR，但是不是当期定盘，而是上一期定盘的 LIBOR。

市场上流动性强的 cap 以美元、欧元和日元计价，每个 cap 都一连串 caplet 组成

• USD cap 每年由 4 个 caplet 组成，每个 caplet 期限是 3 个月，以 USD LIBOR 3M 作标的利率

• EUR cap 每年由 2 个 caplet 组成，每个 caplet 期限是 6 个月，以 EUR EURIBOR 6M 作标的利率

• JPY cap 每年由 2 个 caplet 组成，每个 caplet 期限是 6 个月，以 JPY LIBOR 6M 作标的利率

Swaption 的定义如下：

在利率掉期期权 (interest rate swaption) 合约下，买卖方将同意以下内容：

• 买方付出期权金 (premium) 便有权利 (right) 去行使，而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务

• 支付类掉期期权 (payer swaption)：买方有权利在期权到期日获得一个“支付固定利率接受浮动利率 (pay fixed receive floating) 的利率掉期”，而卖方一旦被行使期权时，则有义务将上述利率掉期给买方

• 接受类掉期期权 (payer swaption)：买方有权利在期权到期日获得一个“接受固定利率支付浮动利率 (receive fixed pay floating) 的利率掉期”，而卖方一旦被行使期权时，则有义务将上述利率掉期给买方

其中利率掉期 (interest rate swap, IRS) 是指交易双方以一定的名义本金为基础，将该本金产生的一种利率计算的利息收入 (支出) 与另一种利率计算的利息收入 (支出)。交换的只是不同特征的利息，没有实质本金的互换。

市场上流动性强的以美元、欧元和日元计价的 swaption。其实 swaption 波动率是一个立方 (cube)，有行权利率、期权到期日、掉期到期日这三个维度。通常我们用的最多的是 ATM swaption 波动率，当行权利率等于远期掉期率，那么波动率立方降维成一个波动率平面，维度为二维。

 

市场数据

 

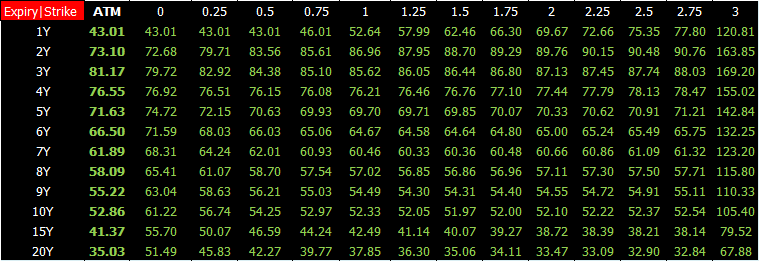
某天的 JPY cap 的真实数据如下：

上图数据又称 cap 波动率平面，它是二维数据结构

 

• 行对应的年限 (expiry)，期权年限从 1 年到 20 年

• 列对应的行权利率 (strike rate)，注意第一列绿色粗体是 ATM 波动率，而每个年限对应的 ATM 行权利率都不同

• 波动率与行权价格和年限有关，可写成 σ(K, T)

• 波动率单位是%，43.01 实际上指的是 43.01%

• 市场波动率带进 Black 公式得到利率上限的市场价格

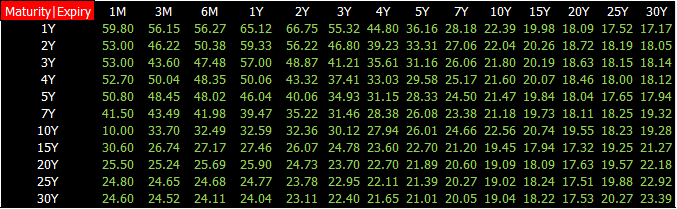
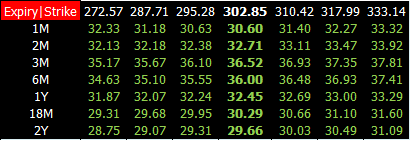
某天的 USD ATM swaption 的真实数据如下：

上图数据又称 ATMswaption 波动率平面，它是二维数据结构

• 行对应的利率掉期的年限 (maturity)，年限从 1 年到 30 年

• 列对应的掉期期权的年限 (expiry)，年限从 1 个月到 30 年

• ATM 波动率与期权年限和掉期年限有关，可写成 σ(T_O,T_U)

• 波动率单位是%，59.80 实际上指的是 59.80%

• 市场波动率带进 Black 公式得到掉期期权的市场价格

3.3

市场价格和模型价格

定义 T₀ < T₁ < … < T_k < … < T_N 是 cap 的年限结构，那么定义

    {T₀, T₁, …, T_N-1} = LIBOR 定盘日

    {T₁, T₂, …, T_N} = 支付日

    N = caplet 的个数

    τ_k = T_k – T_k-1

 

Cap 市场价格

Cap 市场价格是之后模型校正的基准 (benchmark)。关于 Black 模型的 cap 推导细节，可以参考 Interest Rate Model – Theory and Practice, Chapter 1 and Appendix D

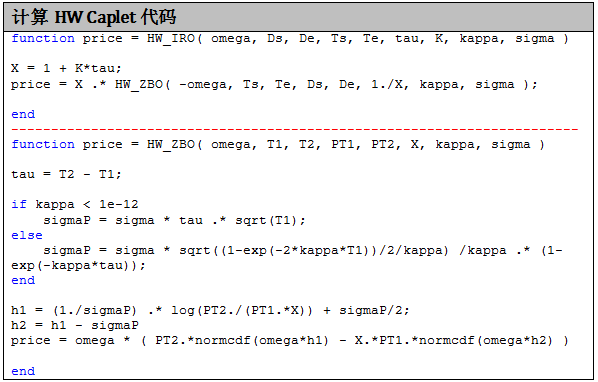
Cap 模型价格

当模型参数为常数时，关于 HW 模型的 cap 推导细节，可以参考 Interest Rate Model – Theory and Practice, Chapter 3

定义 T₀ < T₁ < … < T_k < … < T_N 是 swaption 的年限结构，那么定义

    T_O = swaption 到期日

    T_U = swap 到期日

    τ_k = T_k – T_k-1

Swaption 市场价格

Swaption 市场价格是之后模型校正的基准 (benchmark)。关于 Black 模型的Swaption 推导细节，可以参考 Interest Rate Model – Theory and Practice, Chapter 1 and Appendix D

Swaption 模型价格

Swaption 可看成在期权到期日 T₁ 时交换 IRS 的固定端和浮动端，因此它在 T₁的支付函数为

由小节 2.1 可知 P(t,T;x) 是 x 的减函数，因此定义一个临界值 x* 使得

根据 Jamshidian trick，swaption 只有在 w∙x(T₁) > w∙x* 时才有 payout，为了简化符号引进 P_1,k(x) = P(T₁,T_k;x)，我们有

最后 swaption 在 T₁ 的 payout 可表示为一系列的零息债券期权 (zero-coupon bond option, ZBO) 在 T₁ 的 payout，因此其价值为这些 ZBO 价值的组合。

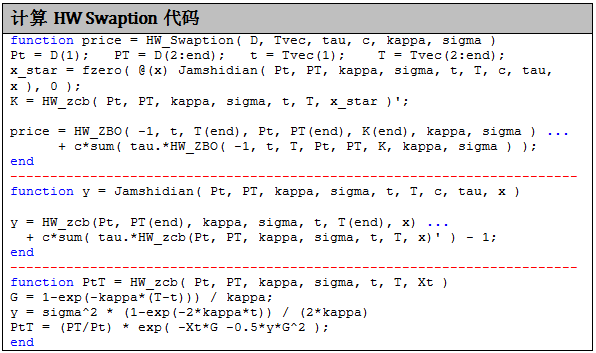
关于 HW 模型的 swaption 推导细节，可以参考 Interest Rate Modeling – Volumn II, Term Structure Model, Chapter 10,10.1.3

3.4

模型校正 (cap)

在 cap 市场上，对每个标准 K 有 n 个到期的 cap，到期日分别为

  

    0 = T₀ < T₁ < … < T_i < … < T_n 

而对于每个 T_i ，cap 的行权价格为 K₁, …, K_j, …, K_m。  

接下来我们分别讨论当模型参数为常数和分段常数是的校正过程。

常数型参数

当参数为常数时，HW 模型校正本质上是找到“最优” κ 和 σ，从而最小化一系列 cap 的市场价格和模型价格之间的差异，其目标函数为：

分段常数型参数

 

从小节 2.3 的公式出发，

• 用上标 i 表示每个 K 下的第 i 个 cap

• 用 N_i 表示该 cap 里面 caplet 的个数

• 用 t_Ni 代表第 i 个 cap 到期日，t_Ni = T_i

当参数为分段常数时，假设选取 ATM cap 做校正，那么 HW 模型校正的步骤为：

1. 参数 κ 根据历史数据手动输入，或者用常数形式的 HW 模型校正得出

   
   

2. 对第 1 个 cap，反解 σ₁ 使得 Cap_mkt(T₁) = Cap¹_HW(σ₁)

   
   

3. 对第 2 个 cap，已知 σ₁，反解 σ₂ 使得 Capmkt(T₂) = Cap²_HW(σ₁,σ₂)

   
   

4. 重复上面过程到第 n 个 cap，已知 σ₁,σ₂,…,σ_n-1，反解 σ_n 使得 Capmkt(T_n) = Capⁿ_HW(σ₁,σ₂,…,σ_n-1,σ_n) 

以上过程把 1 个 n 维的优化问题转成 n 个 1 维的优化问题，增加了模型校正的效率。需要注意的是，上述步骤并不是每次都行得通，这种情况称为“波动率紧缩 (volatility squeeze)”，出现在当 T_i+1 到期的 cap 比 T_i 到期的 cap 价格小很多的时候。这种情况很少见，一旦出现可以当成是套利的信号。

3.5

模型校正 (swaption)

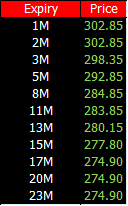
在 ATM swaption 市场上，在以下的年限结构上考虑一串特殊的 swaption

 

    0 = T₀ < T₁ < … < T_i < … < T_n 

此类 swaption 的 option 到期日为 T_i,  i =1, 2, …, n-1，而它们的 swap 到期日都是 T_n，这样的 swaption 成为 coterminal swaption，记作 aYbY，指的是 a 年 option 到期可以换一个 b 年 swap 的 swaption。

由于此类结构和市场交易的百慕大期权 (Bermudan swaption) 很类似，因此 coterminal swaption 经常被当作校正工具来使用。

接下来我们分别讨论当模型参数为常数和分段常数是的校正过程。

常数型参数

当参数为常数时，HW 模型校正本质上是找到“最优” κ 和 σ，从而最小化一系列 coterminal swaption 的市场价格和模型价格之间的差异，其目标函数为：

分段常数型参数

当参数为分段常数时，假设选取 ATM coterminal swaption 做校正，那么 HW 模型校正的步骤为：

1. 参数 κ 根据历史数据手动输入，或者用常数形式的 HW 模型校正得出

   
   

2. 对第 1 个 swaption，反解 σ₁ 使得 Swaption_mkt(T₁) = Swaption¹_HW(σ₁)

   
   

3. 对第 2 个 swaption，已知 σ₁，反解 σ₂ 使得 Swaptionmkt(T₂) = Swaption²_HW(σ₁,σ₂)

   
   

4. 重复上面过程到第 n-1 个 swaption，已知 σ₁,σ₂,…,σ_n-2，反解 σ_n-1 使得 Swaptionmkt(T_n-1) = Swaption^n-1_HW(σ₁,σ₂,…,σ_n-2,σ_n-1) 

和 cap 校正是遇到的问题一样，波动率紧缩也是 swaption 的校正可能出现的问题。该情况出现在当 T_i+1 到期的 swaption 比 T_i 到期的 swaption 价格小很多的时候。这种情况很少见，一旦出现可以当成是套利的信号。

3.6

校正结果

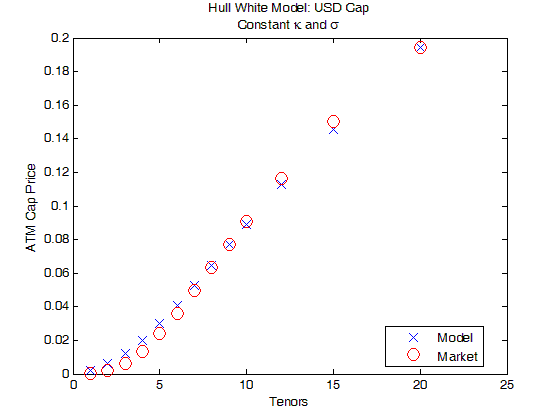
下图展示着当 κ 和 σ 为常数时，USD ATM cap 的市场价格 (红圈) 和模型价格 (蓝线)，发现它们在不同 T 时结果相近但不完全吻合，原因是 2 个未知量来拟合 13 个 cap，只能平均接近不能各个匹配。

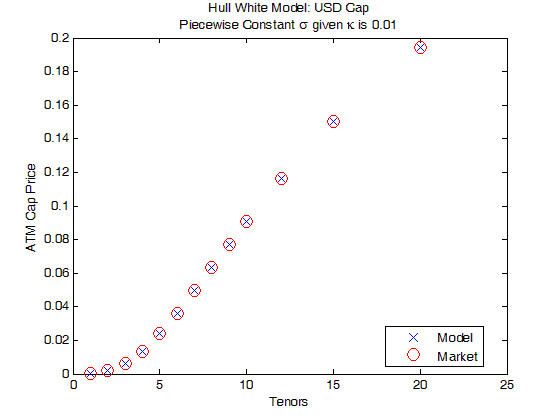
下图展示着当 κ 为已设好的 0.01 和 σ(t) 为分段常数时，USD ATM cap 的市场价格(红圈) 和模型价格 (蓝线)，发现它们在不同 T 时完全吻合，原因是当 κ 已知，每个 cap 和 σ 是一一对应关系。

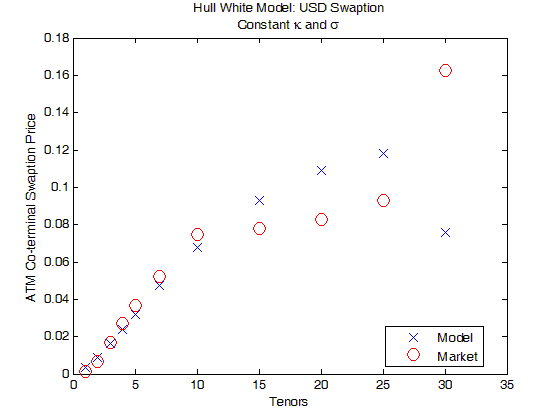
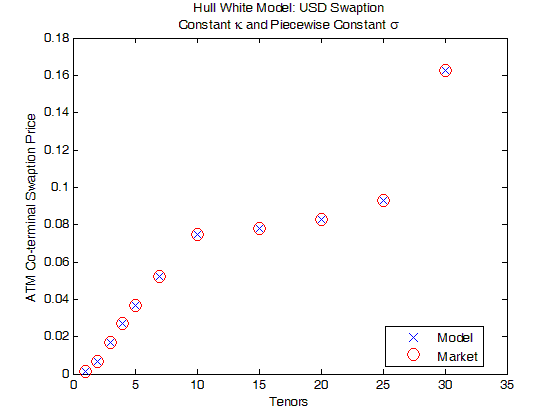
下图展示着当 κ 和 σ 为常数时，USD ATM coterminal swaption 的市场价格 (红圈) 和模型价格 (蓝线)，发现它们在短期 T 时结果相近但长期 T 相差很远。原因是 2 个未知量来拟合 11 个 swaption，只能平均接近不能各个匹配，而且后面几个 swaption 的到期日从15 年到 30 年，常数参数很难能把这么长的掉期期权拟合好。

下图展示着当 κ 为常数和 σ(t) 为分段常数时，USD ATM coterminal swaption 的市场价格 (红圈) 和模型价格 (蓝线)，发现它们在不同 T 时完全吻合，原因是当 κ  先校正好，每个 swaption 和 σ 是一一对应关系。

第四章 - 商品类

4.1

Schwartz 模型

模型介绍

股权类的 Black-Scholes 模型也适用于商品类，但是它无法处理具有均值回归 (mean-reverting) 特征的商品。为解决上述缺点，一个方法就是将均值回归特征融合到商品价格过程中，而 Schwartz 模型涵盖这些特点。

商品类的 Schwartz (SW) 模型下的 SDE 是描述商品即期价格 (commodity spot price) 的走势：

Eduardo S. Schwartz 在 1997 年提出此模型，其论文题目是

The Stochastic Behavior of Commodity Prices Implications for Valuation and Hedging

模型参数

 

一般情况下

• r(t) 当成常数

• κ(t) 和 σ(t) 当成常数

• θ(t) 当成分段常数

 

它们的获取方式为

• r: 根据商品结算的货币，绝大部分情况是 USD，用其掉期曲线 USD Libor 3M 曲线，在曲线上插出 T 点的 r 值

• κ 和 σ: 从一系列商品期货欧式期权中校正出来

• θ(t): 从商品期货曲线中校正出来

4.2

市场标准产品和数据

产品定义

商品类市场标准产品是一系列“不同行权价格 K 和不同年限 T 商品欧式期货期权 (CM futures option)”，定义如下：

在商品欧式期货期权 (commodity futures option) 合约下，买方和卖方将同意以下内容：

 

• 期权买方付出期权金 (premium) 便有权利 (right) 去行使，而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务。

• 看涨期权：买方有权利在到期日以 K 买入期货，而卖方一旦被行使期权时，则有义务以 K 卖出期货

• 看跌期权：买方有权利在到期日以 K 卖出期货，而卖方一旦被行使期权时，则有义务以 K 买入期货

 

其中K是执行价格 (strike price)。

市场数据

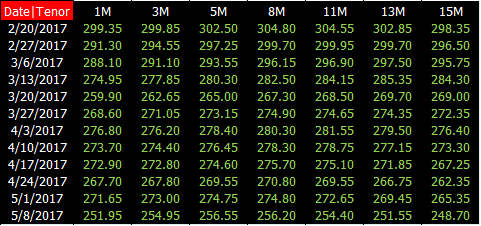
某天的咖啡期货期权和期货价格的真实数据如下：

上图数据又称 CM futures option 波动率平面，它是二维数据结构

 

• 行对应的年限 (expiry)，期权年限从 1 个月到 2 年

• 行对应的行权价格 (strike)，注意第四行白色粗体 302.85 是 ATM 行权价格，其对应的绿色粗体是 ATM 波动率

• 波动率单位是%，32.33 实际上指的是 32.33%

• 市场波动率带进 Black 公式得到期货期权的市场价格

上图数据又称 CM futures 价格曲线，它是一维数据结构，每一个年限对应一个期货价格。

4.3

市场价格和模型价格

市场价格

CM futures option 的市场价格是之后模型校正的基准 (benchmark)。关于 Black模型的 CM futures option 推导细节，可以参考 Commodities and Commodity Derivatives Modeling and Pricing for Agriculturals, Metals and Energy, Chapter 4

模型价格

给定 κ 和 σ，通过 Ito’s lemma 可以推出 F(0,T) 在 SW 模型下的表达式以及它的SDE：

从上面的 SDE 发现参数 θ(t) 不见了，而且在 SW 模型下 F_SW(0,T) 的分布和 Black 模型下的分布非常相似，不同的只是离散项。因此，套用 Black 模型的公式，类比出 CM futures option 的定价公式：

4.4

模型校正

SW 模型校正步骤总结如下：

1. 先假设 F_SW(0,T_i) = F(0,T_i), 从一系列欧式期货期权校正出 σ 和 κ

2. 再使得 F_SW(0,T_i) = F(0,T_i), 从期货曲线进行校正出 θ(t)

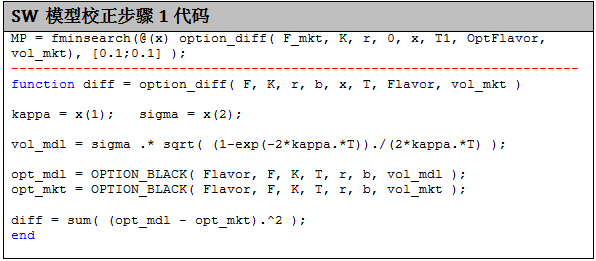
步骤 1

SW 模型校正本质上是找到“最优” κ 和 σ，从而最小化一系列 ATM CM futures option 的市场价格和模型价格之间的差异，其目标函数为：

步骤 2

在 SW 模型下定价 CM futures option 时不需要 θ，因为 F 是从期货曲线中提取的。在确定了 σ 和 κ 之后，再校正 θ(t) 从而完全匹配期货的市场价格和模型价格，其目标函数为：

假设 θ(t) 为分段常数，令 θ(t)= θ_i 当 t 属于 [T_i-1,T_i)。令 F_i = F_mkt(0,T_i)

4.5

季节性调整

与典型的投资性资产相比，农产品的价格通常显示出季节性特征。在旺季时，农产品的产量会剧增而导致价格下降。之后，农产品价格通常会逐渐上涨，当然这也取决农产品不可预见的存储量。因此，在对农产品价格进行建模时会考虑季节性因素。对那些长期期权进行定价时，季节性因素显得更为重要。

为了在商品价格过程中体现季节性因素的影响，通常会用一个函数来对“季节性的贡献”进行建模。说明如下：

带季节性调整的 SW 模型校正步骤总结如下：

 

1. 用 Kalman Filter 和 m 个期货校正季节性函数的 β­ 和 ψ

   
   

2. 最小化一系列欧式期货期权的市场价格和模型价格得出 κ 和 σ

   
   

3. 最小化一系列期货曲线的市场价格和模型价格得出 θ(t)

 

上述步骤 2 和 3 和不带季节性调整的 SW 模型步骤 1 和 2 一样 (见小节 3.4)，不同的是期权公式里面的 F_SW(0,T) 要做季节性调整。

因此在上面校正过程之前，我们必须知道季节函数 f 里面的参数 β 和 ψ，而校正它们用的是 Kalman Filter (KF) 方法。

4.6

Kalman Filter 方法

为了节省空间，将时间 t 写成下标，比如 S(t) 写成 S_t，F(t, T) 写成 Ft,T，定义

 

    xt = lnSt = 现货价格对数

    yt = lnFt,T + fT = 期货价格对数

根据以上符号和 SW 模型可推出以下两个线性方程：

上面两个方程：

 

• E2 是一个观察方程，它将列向量 yt 和标量 xt，解释列向量 ct 和误差列向量 et 联系起来

• E1 是一个动态方程，它描述一个一阶马可夫链 (Markov chain) 过程。变量Tt,Rt, Qt, Zt 和 Ht 称为系统变量，它们是关于 SW 模型参数的函数

                       

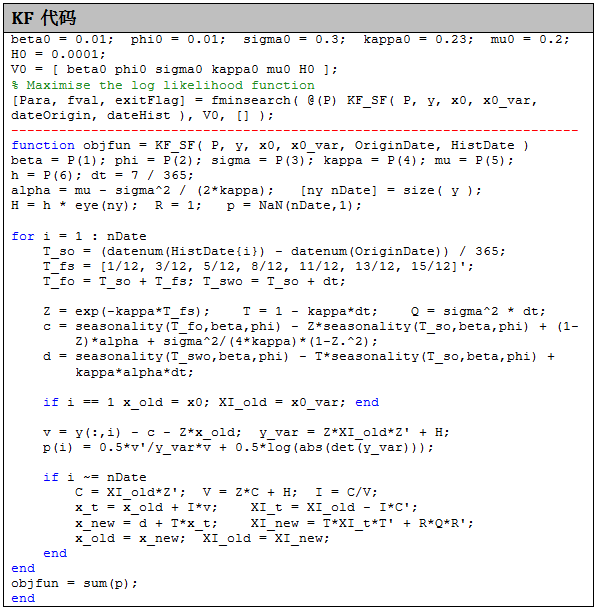
在 KF 校正过程中需要不同期限期货的历史价格，如下图所示

• 每行代表不同天数上的期货价格 (每隔 7 天)

• 每列代表不同期限的期货价格 (1 个月、3 个月到 15 个月)

KF 方法是在已知数据 Yt = {y1, y2,…, yt} 和相关模型的情况下，更新 xt+1 条件分布。因为条件分布是一个正态分布过程，用条件均值和协方差矩阵就足以说明此过程。

将 xj|i 和 Σj|i 定义在已知 Yi 的情况下 xj 的条件均值和协方差矩阵，我们有

    xj | Yi ~ N(xj|i, Σj|i)

做好准备工作

• 算出起始值 x1|0 和 Σ1|0

• 确定初始值 σ, κ, μ, θ, H (为了简化，假设 H 对角线上值是一样的)

• 初始化对数密度概率函数 p = 0

KF 算法描述如下：

最后最大化 p 来得到 β*, ψ*, σ*, κ*, µ*, H*。关于以上 Kalman Filter 校正步骤，可以参考 Analysis of Financial Time Series, Chapter 11

第五章 - 外汇类

5.1

Heston 模型

模型介绍

虽然 Black-Scholes 模型在市场上被广泛应用于定价欧式期权，该模型假设波动性是常数或是时间 t 的函数。从实证证据可以看出，这一假设是错的，资产的波动率也表现出随机性，就像资产价格一样。而 Heston 模型在 Black-Scholes 模型基础上把波动率看成是个随机变量。

股权类的 Heston 模型下的 2 个 SDE 分别描述即期汇率 (spot FX rate) 和其波动率 (volatility) 的走势：

Steven L. Heston 在 1993 年提出此模型，其论文题目是

A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options

模型参数

一般情况下

• r_d(t) 和 r_f(t) 当成常数

• v0 当成常数

• κ(t), θ(t), η(t) 和 ρ(t) 可以是常数，但通常是分段常数

它们的获取方式为

• r_d(r_f): 本币(外币)曲线，如果美元对应 USD Libor 3M 曲线，如果非美元对应其 FX 曲线，在曲线上插出 T 点的 r_d(r_f) 值

• v0, κ或κ(t), θ或θ(t), η或η(t), ρ或ρ(t): 从一系列外汇欧式期权中校正出来

5.2

市场标准产品和数据

产品定义

 

外汇类市场标准产品是一系列“不同价内价外 Delta 和不同年限 T 外汇欧式期权 (FX option)”，定义如下：

用 FOR 代表外币，DOM 代表本币，FOR/DOM 为货币对。期权买方和卖方进入外汇欧式期权 (FX vanilla option) 合约的将同意以下内容：

 

• 买方付出期权金 (premium) 便有权利 (right) 去行使，而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务。

• 看涨 FOR/DOM 期权 (看涨外币看跌本币)：买方有权利在到期日进入当前即期市场买入外币 N，并卖出本币 N×K；而卖方一旦被行使期权时，则有义务卖出外币 N，并买入本币 N×K

• 看跌 FOR/DOM 期权 (看跌外币看涨本币)：买方有权利在到期日进入当前即期市场卖出外币 N，并买入本币 N×K ；而卖方一旦被行使期权时，则有义务买入外币 N，并卖出本币 N×K

 

其中 N 是名义金额 (notional)，K 是执行汇率 (strike rate)。

市场数据

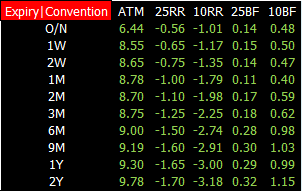
某天的 EURUSD 期权的真实数据如下：

上图数据又称 FX option 波动率平面，它是二维数据结构

• 行对应的年限 (expiry)，期权年限从 1 天到 2 年

• 行对应的报价惯例 (convention)，外汇市场最常见的报价类型是价中(ATM)，25 和 10 风险反转 (risk reversal, RR) 组合，25 和 10 蝶式 (butterfly, BF) 组合

• 波动率单位是%，6.44 实际上指的是 6.44%

• 市场波动率带进 BS 公式得到期权的市场价格

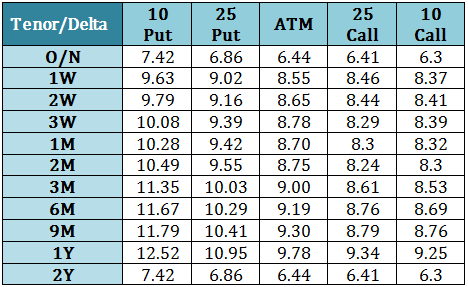
下表根据 ATM, RR 和 BF 之间波动率的联系推出 10 和 25 delta 对应的波动率：

利用上表右边的公式算出各个 delta 和 T 下的波动率。

5.3

市场价格和模型价格

市场价格

 

FX option 的市场价格是之后模型校正的基准 (benchmark)。关于 BS 模型的 FX option 公式推导细节，可参考 Foreign Exchange Option Pricing - A Practitioner's Guide, Chapter 2

模型价格

当模型参数为常数时，关于 Heston 模型的 option 推导细节，可以参考 The Heston Model and Its Extensions in Matlab and C#, Chapter 1

 

当参数为分段常数时，表达如下：

为了简化公式，用 W_k 代表 Heston 模型参数集，即

    Wk = {κk, θk, ηk, ρk}

当模型参数为分段常数时，关于 Heston 模型的 option 推导细节，可以参考 The Heston Model and Its Extensions in Matlab and C#, Chapter 9

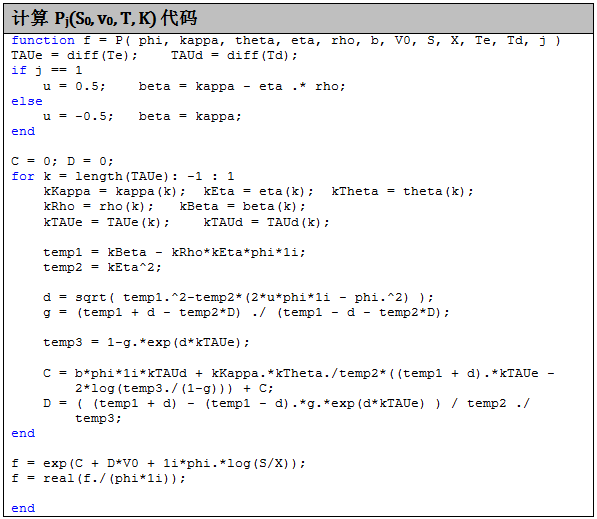
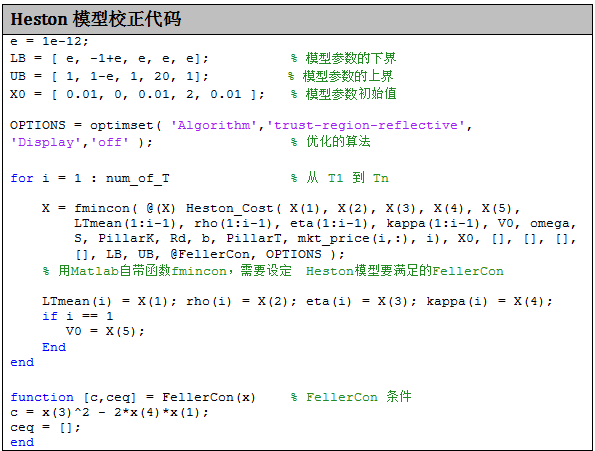
上面公式难点就是如何用迭代的方法求得 C 和 D，最后计算出 P，代码如下：

5.4

模型校正

在外汇期权市场上，对每个标准 delta 有 n 个到期的 option，到期日分别为

    0 = T₀ < T₁ < … < Tk < … < T_n 

而对于每个 Tk ，option 的行权价格为 K_1,k, …, K_j,k, …, K_m,k。

接下来我们分别讨论当模型参数为常数和分段常数是的校正过程。

 

常数型参数

 

当参数为常数时，Heston 模型校正本质上是找到“最优”  v0, κ, θ, η 和 ρ ，从而最小化一系列 FX option 市场价格和模型价格之间的差异，其目标函数为：

分段常数型参数

当参数为分段常数时，假设选取整个 option 波动率平面做校正，那么 Heston 模型校正的步骤为：

1. 参数 v0 是用常数形式的 Heston 模型校正而得出

   
   

2. 在 T₁ 时，反解 W1 = {κ1, θ1, η1, ρ1} 最小化下面目标函数

   
   

   
   

3. 在 T₂ 时，已知 W1，反解 W2 = {κ2, θ2, η2, ρ2} 最小化下面目标函数

   
   

   
   

4. 重复上面过程到 T_n，已知 W1,W2,…,Wn-1，反解 Wn = {κn, θn, ηn, ρn} 最小化下面目标函数

   
   

5.5

校正结果

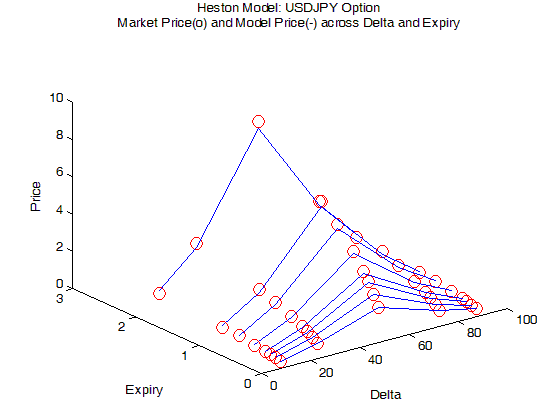
下图展示着 USDJPY option 的市场价格 (红圈) 和模型价格 (蓝线)，发现它们在不同 delta 和 T 时差别不大。

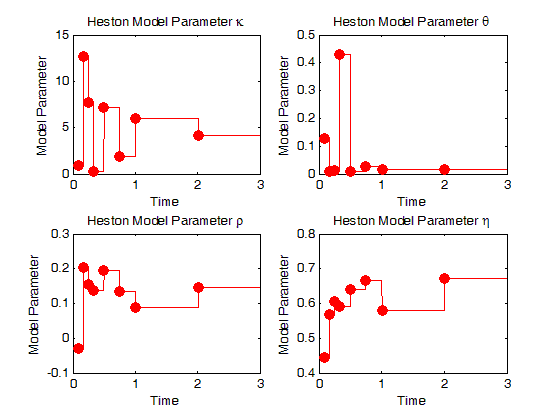
下图展示着模型参数的分段常数形式，发现它们都不是和时间 t 呈单调关系，但除了 κ 上下摇摆而变化很大之外，其他三个参数总体来讲还比较稳定。

总结

模型校正是选择模型中的参数使得市场流动性强的交易价格 (市场价格) 和模型输出 (模型价格) 完全匹配或尽可能接近。完全匹配价格意味着消除套利机会。

几乎所有的金融模型都有一些不能准确测量的参数。在最简单 Black-Scholes 模型，该参数是波动率。如果我们无法测量该参数，我们如何决定波动率的值？如果决定不了，那么该模型是无用的。

两种方式可以得到波动率的值。一个是使用历史数据，另一个是使用当天的期权价格数据。

• 历史波动率：它的主要问题是使用过去的数据向后看而未来无关。另一个问题是，它可能给出一个和市场价格不一致的价格。例如你有兴趣购买一个期权。你根据历史波动率算出的价格是 10 美元，然而该期权的市场价格是 19 美元。你还有兴趣购买吗？这时候，要不期权市价错了，要不你对波动率的估计的不正确。

• 隐含波动率：它是隐含在市场交易产品的价格里面。在上面的例子中，我们要问什么波动率放入 Black-Scholes 以获得 19 美元的“正确”价格。然后使用该波动率来定价其他复杂产品。这时我们是向前看的，而不是用来自过去的信息。

在量化金融上，第二种叫做模型校正，第一种不是。

模型校正使得市场流动性强的交易价格接近模型价格，但是这些产品的市场价格已经有了，为何还需要模型价格呢？请注意，模型校正从来不是为了定价那些有市价的简单产品，而且为了定价那些没有市价的复杂产品。但是，一个模型连一个简单产品的价格都算不准，谁还会对它算准一个复杂产品有信心呢？理清这个就知道模型校正的意义了。本文只是讲了模型校正的基本知识，此外：

• 模型校正在实际应用上还会有许多变种，目标函数除了最小化绝对价格，还有最小化相对价格或绝对波动率，它们各有优缺点限于篇幅就不延伸了。

• 模型校正和机器学习也有同异，相同之处是它们最终都是用“最小化代价函数技巧”来解决问题；不同之处是前者用数量少的当前数据，而后者用数量多的历史数据。

• 模型校正也可以用于量化交易上，比如校正一个均值回归例如 Hull-White 模型加上 Kalman Filter 方法可以用于配对交易 (pairs trading)。

• 模型校正还有更有挑战的内容，比如 Libor Market+SABR 模型、Local Stochastic Volatility 模型，这些内容是量化金融的巅峰，等我哪天没工作了才有精力和勇气来写 :)