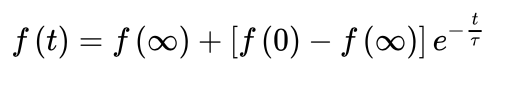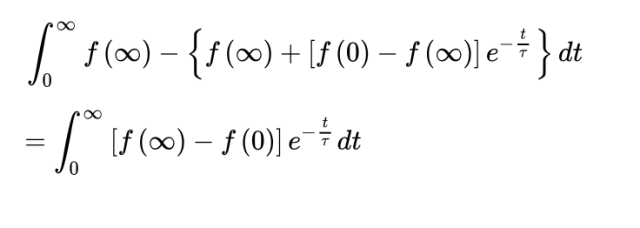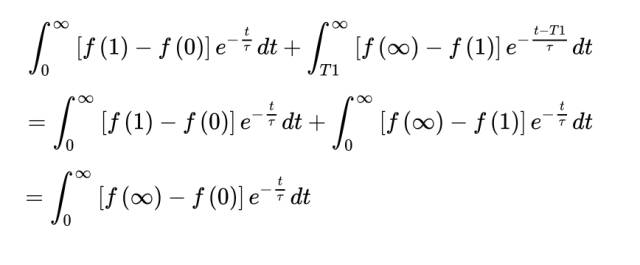做数学题比统一世界更爽,你会怎么做呢?
朋友,你知道模拟电路中的换路定律吗?
>>>>
换路定律的内容是这样的——
「如果你在一个含有电容的电路中,突然改变电路的状态,那么这个电容两端的电压并不会突变,而是会连续地,先快后慢地回归到电路后来的状态。」
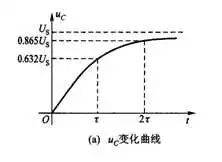
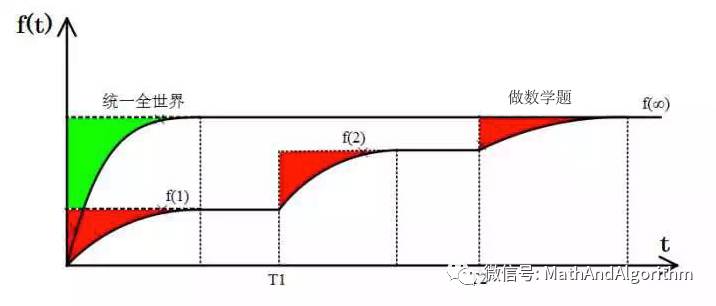
这个回归的过程大概是这个样子的:
一阶电路的全响应
在这篇回答里,我们将会在换路定律的基础上,用数学去证明,为什么这个问题下大多数的「统治世界奴役人类」的答案,其实并不是最优解。
首先要说明一件事情。
我们人生中快乐的来源,并不是我们在符合现有预期下的享受,而是我们对一件件事情的那种预期升高的过程。
换句话说,那些带给你开心的,并不是你的「位置」,而是你的「位移」。
你努力学习当上学霸,当得久了,习惯了学霸的生活,预期也慢慢调整成了学霸的预期.
你也会重新开始为了自己只是第三而不是第一而烦恼,会为了距离清北还差两步的距离而着急,会产生很多新的问题让你头疼。
在这个过程中,其实你最快乐的,是你一开始成绩飞速提升的那段过程。
你揭竿而起当上皇帝,当得久了,习惯了皇帝的地位,预期也慢慢调整成了皇帝的预期。
你也会重新开始为了百废待兴的朝政而烦恼,会为了自己各怀鬼胎的文武百官而发愁,会有一堆新的问题让你头疼。
在这个过程中,其实你最爽的,是你一开始招兵买马攻城略地的那段过程。
类似的例子还有很多:你买了一个新书包,它的体验高于使用旧书包时你所习惯的预期,所以你每用它一次就会开心一下。
但随着你的预期升高,你从中获得的快感也会慢慢降低;
再比如你升了职,它的体验比你在原职时习惯的预期要高,你每次看到同事对你尊敬的眼神,每次领到比原来更高的薪水,都会体验到这种升差带来的快感。
但久而久之,你会慢慢适应新职位,看到同事的尊敬也会觉得理所当然。
在这个过程中,影响我们快感的因素有哪些呢?
1.我们之前的处境有多惨;
2.我们后来的处境有多好;
3.适应这个变化所需要的时间。
在处境上,我们前后的「升差」越大,带来的快感也就越大。
从职员升到组长,当然不如从职员直升总经理要来得爽。
在适应时间上:比如你适应「同事尊敬的眼神」可能就比适应「更高的薪水」要快。
因为前者每天都接触好多次,在这样的频率下预期早就更新了,而后者每个月才接触一次,可能会让你高兴好久。
当然,有些人会举反例——比如相爱的人天天作伴就是爽,被人折磨虐待就是惨,无法适应。
这是因为我们的预期既有短期的成分,也有长期的成分:
比如相爱的人作伴或者被肉体折磨,它完全适应的时间就几乎是无限长,因为它触及到最长期的成分——
就是我们作为一个生物的本能,这种预期是难以动摇的。
而这三个因素,正好就是分析换路后电路状态的「一阶电路全响应的三要素」!
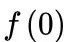
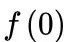
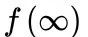
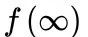
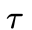
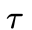
最后,在电路换路之后,系统的输出(我们的预期变化)就是这个公式:
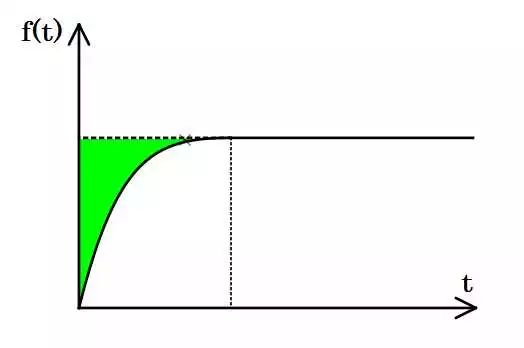
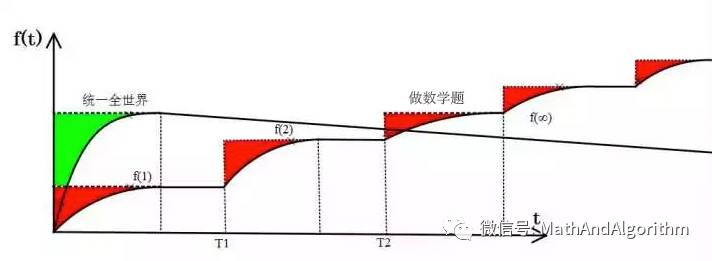
而画出来,我们每次得到的快感,就是下面这张图中的绿色部分面积——
体验变化带来的快感
在一开始的时候,你的预期提升迅速,获得的快感也就强烈;
而到了后期,你的实际体验和预期相差无几了,带来的快感也就越来越少。
总之,从开始到结束,按照时间把这个心理升差积分起来的绿色部分面积,就是下面这个式子:
那又怎样?
这个时候,可能就会产生两种分配享受的模式。
一种是「一步登天型」,一种是「细水长流型」。
一步登天型:一次性爽个够,比如获得超能力之后,就马上统一世界,奴役全人类。
下面取最典型的例子,用「统一全世界」代替;
细水长流型:慢慢地享受境遇的提升,比如慢慢积累财富,然后投入到对人类有益的事业。
下面取最典型的例子,用做数学题代替;
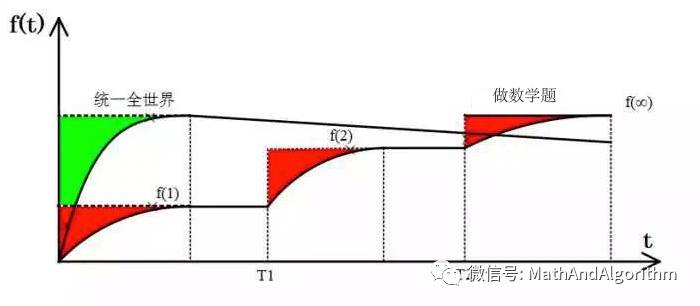
如果我们只考虑分配模式带来的区别,也就是假设三个要素都一样,只是分配方式不同,这两个过程的「总快乐值」是怎样的呢?
"统一全世界" 和 "做数学题" 的对比
这个时候,我们假设我们的升差被分成了几份(图中是三份,但是我们为了计算简便,计算时只考虑两份)。
这个时候,被分成两份的升差,积分出来的面积会是怎样的呢?
咳。还是一样嘛。
也就是说,分配方式的不同,本身并不会导致快乐总量的区别。
分配成两部分是一样的结果,显然分配成三个或更多的部分,结果也不会变。
这下麻烦了,结果居然是一样的,我还怎么去证明做数学题比统一全世界更快乐呢?
下面进入文科生部分!
还是有办法的。
我们在前面比较分配模式的时候,有一个假设——这两种方案最终能达到的上限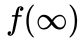
但其实是不一样的。
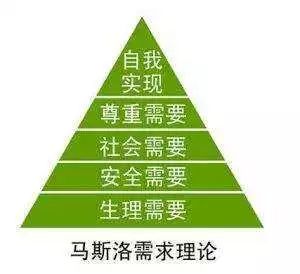
(已经被说烂了的)马斯洛的需求层次理论告诉我们,
我们人生的追求,主要分为这五个层次——
一般而言,越是高层次的追求,能够实现它的人便越少。
一个人实现了一个层次的追求,便会转而追求下一个层次,否则往往无暇奢求下一层次的需要。
而统一全世界能够实现什么需求呢?
你会:
衣食无忧(生理需要);
天下无敌(安全需要);
妻妾成群(社会需要);
万众膜拜(尊重需要);
最后还可以实现一下你的皇帝梦(自我实现需要)
这就是这个问题下其他答主主要答的点。
但是,这种满足,是没有前途的。
为什么呢?
有一首诗,叫做《山坡羊·十不足》是这么说的:
逐日奔忙只为饥,才得有食又思衣。
置下绫罗身上穿,抬头却嫌房屋低。
盖了高楼并大厦,床前缺少美貌妻。
娇妻美妾都娶下,又虑出门没马骑。
将钱买下高头马,马前马后少跟随。
家人招下十数个,有钱没势被人欺。
一铨铨到知县位,又说官小职位卑。
一攀攀到阁老位,每日思想要登基。
一朝南面坐天下,又想神仙下象棋。
洞宾陪他把棋下,又问哪是上天梯?
上天梯子未做下,阎王发牌鬼来催。
若非此人大限到,上到天上还嫌低。
——朱载堉《山坡羊·十不足》
描绘的就是人的这种欲壑难填的心理。
但是,最悲剧的是,你作为世界之王,却永远只能停留在「一朝南面坐天下,又想神仙下象棋」的阶段。
你就算天下无敌,你也只能做到这样了。
这个社会的发展活力已经被你的统治彻底挖空,再也发展不出什么更先进的东西了。
你三年后是万众膜拜妻妾成群,五年后还是万众膜拜妻妾成群,十年后还是万众膜拜妻妾成群,五十年,一百年后,还是万众膜拜妻妾成群。
没有神仙来陪你下象棋。
没有神仙来陪你下象棋。
没有神仙来陪你下象棋。
我之前并没有提到——其实「体验变好获得快乐」这种事情本身,也是一种体验。
也就是说,不仅体验的导数会影响你的快乐,它的二阶导数也会。
对于曾经体验过一步登天的,适应了疯狂涌出的多巴胺的你,忽然进入了这样一种死气沉沉毫无希望的境地,你会有什么体验?
统一世界是很无聊的!
在无数的奴隶和美女中间,你会慢慢地玩腻,获得的快感反而会慢慢降低。
我们前面知道,分成多部分的变化,产生的快感值是等效的,缓慢降低也同样,会产生同样的负的快感(只不过在图中不好画)。
这类似于吸毒,你体验过极致的快感后,看什么都会觉得闷,觉得无味,反而增加了痛苦。
而做数学题呢?
它在「自我实现」这个层面的上升空间,几乎是无穷的。
如果你采用第二种策略——
在不破坏社会的情况下慢慢积累知识与能力,然后发展对社会有益的事业,你会看到什么呢?
三年之后,你可能会看到你的行为让你身边各个专业的大学同学都能找到复习的捷径。
你能看到学物理,生物,经济,建筑,心理学的学生,在图书馆做着同样的数学书戴着耳机看着算法与数学之美;
五年之后,你可能会看到你的行为真的改变了中国的教育,让千千万万的学生能够弥补一部分阶级差异,教育资源带来的天堑。
你可以在新闻联播上看到四线小镇的居民家里,一个小孩捧着手机,学着研究算法与数学之美;
十年之后,你可能会看到你的行为开始不仅仅是一个交流数学知识的网络平台,它还能够走向世界,还能够学到绝不仅限于课本的各种知识。
你还能体验荒野求生,看到贝爷在你的APP里面讲解某种虫子的正态分布;
五十年之后,你可能会体验到你的行为掀起的教育革命,一个人在学习中从读取,到理解,到存储,到整理的学习流程中,人类所有的心理弱点都将被技术克服。
从地球到月球短短几十分钟的旅行时间里,一个普通人就可以在太空舱中学完一本《电动力学》;
一百年之后,我编不下去了……
总之,在这种情形下,虽然它的快乐来得不如一统天下快,但是,它的上限更高——
做数学题比统一全世界更爽
而我们知道,我们获得的快乐对同样升差的各种分部是相等的,也就是说,第二种策略的快乐总量更高。
因为它更有发展的深度。
所以,我们成功地通过一阶电路的全响应,用数学手段证明了,做数学题比统一全世界更爽。Q.E.D.
最后,如果我拥有以一己之力碾压全地球战力的能力,我会做什么呢?
我会用我的瞬间移动能力,去一天送10000个快递,然后拿赚到的工资,去请更好的老师,录更多的好课;
我会去中东当雇佣兵,去每天悄无声息地击毙一堆ISIS恐怖分子,然后拿赚到的报酬,去请更好的老师,录更多的好课;
我会去亲手活捉通缉令上最臭名昭著的毒枭和逃犯,然后拿赚到的赏金,去请更好的老师,录更多的好课;
所以,当你看到我拖着奄奄一息的毒贩走进警察局的时候,请不要怀疑,我是算法与数学之美粉丝中的一员。
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域。
稿件一经采用,我们将奉上稿酬。
投稿邮箱:math_alg@163.com