从比特币漏洞到完美的事务隔离性

先来看一则近文，2014年3月，曾经的第二大比特币在线银行Flexcoin，因为程序处理并发请求不当，被攻击者找到漏洞，转走了所有在线账户中的比特币，资产和信誉都破产了，被迫一夜之间关门。在这起骇人听闻的攻击中，攻击者首先在Flexcoin上开了一个比特币账户，并且存进了少量的比特币。随后，构造了几千个并发的转账请求，利用了Flexcoin对并发请求的不当处理，使得在转出账户余额不足的情况下，仍然可以转账到目标账户。然后把目标账户中的比特币继续透支转到下一个账户... ...用滚雪球的方式，最后把Flexcoin比特币账户中的所有比特币转走了。

 

 

这一起攻击事件中的漏洞是由于处理数据并发访问不当而造成的。无独有偶，今年（2017年）的另一份测试报告（酸雨测试）显示，12家重要的电商Web平台（提供电商WebApp部署到用户环境，包括开源和商业的形式），在使用低于可串行（serializable）隔离级别的数据库时，都存在处理并发请求不当而造成的各种漏洞。诸如在结算时被偷取商品，重复使用礼品卡、优惠券，破坏库存数据等等。这12家电商平台的使用非常广泛，在超过200万的网站上部署，在所有电商类Web站点中的覆盖率超过50%。

上面两则报道和其他更多的生产实践其实都说明一个问题，正确的实现并发访问数据的程序是非常困难的，具有：

• 开发成本高

• 测试困难

• 故障排查困难

• 一旦出现数据错误造成的后果极其严重

等特点。特别是如果需要针对不同业务，在业务高速发展迭代的过程中实现这些程序，更是容易引入隐秘难以发现的Bug，埋下后果严重的隐患。

所以一直以来数据正确性的保证，其实都是依赖数据库系统。数据库为用户提供“事务”（transaction）的服务，只要用户正确使用事务把业务操作封装起来就可以保证得到的数据总是正确。事务提供的隔离性服务是保证数据正确性的基石之一，它让用户通过数据库访问数据时，可以像只有自己一个人完全独占数据库一样轻松使用。同时执行的多个事务之间被完全隔离。这种完美的隔离性被称作可串行隔离。

数据库产品有时会提供低于可串行的隔离级别供用户使用，包括SQL标准的四个隔离级别，和其他几个后续出现的常用隔离级别，以换取更好的性能。然而这些不完整的隔离服务，再次把部分或全部的并发数据访问难题踢回给了用户，用户再次面临隐秘Bug和数据错误的巨大风险中，就像酸雨测试所揭示的那样。甚至，用户常常对这些风险的存在都没有足够认识，不知道自己的应用和业务有面临这么大的危险。殊不知，问题没有实际出现只是因为并发还不是很高，或者是“运气好”。这其实和数据库厂商的刻意隐瞒和误导宣传有重要关系。下面是酸雨测试报告中提供的一个简化例子:

程序（a）中的代码因为缺乏并发保护，会造成“透支转账”。程序（b）加入了使用事务服务，解决了这个问题。但是当使用的数据库使用较低的隔离级别，低于SQL标准的可重复读（repeatable read）或者是MySQL的可串行化隔离级别时，数据错误的风险依然存在。考虑更加复杂的业务场景，和业务需求的动态变化特性，只有保证完美隔离的可串行化级别才能真正满足用户的需求。

这样的情况不会永远存在下去，互联网应用越来越多，高并发的应用场景和云数据库的商业模式下，“绝对正确的数据”将是用户最高优先级的诉求，而不能讨价还价的（如果用户知道实情的话：））。

这篇文章的目标在于抠一抠事务完美的可串行隔离级别究竟是什么样的，及其背后的理论工具，这些理论工具在处理并发控制问题都十分有用。数据库领域的文献可谓浩如烟海，这篇文章抠出可串行化理论中最核心的部分，希望能为读者带来帮助。

0. 基本概念和符号

为描述准确方便，把几个用到的基本概念和它们的表示方式罗列一下。

0.1 关系

关系（relation）本质是一个集合，一个什么样的集合呢？是全集（domain）S与自身笛卡尔积S×S的一个子集。

举个栗子，全集定义为S=(1，2，3)，全集与自身的笛卡尔积为一个二元组的集合：S×S=((1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3))。S上的小于关系<，是S×S的子集，即：<=((1,2),(1,3),(2,3))。

值得说明一下，这里说的关系指的是二元关系（binary relation），更一般的关系可以是N元关系（N-ary relation），定义为全集S与自身N次笛卡尔积Sⁿ的子集。在没有特别说明时，我们说的关系就是指的二元关系。

0.2 偏序和全序

偏序

偏序（partial order）本质是一个关系，一个什么样的关系呢？

先定义几个关系的属性：

• 自反性（reflexive）: 如果对于每一个x∈S都有(x,x)∈R，则称R具有自反性

• 反自反性（irreflexisve）: 如果对于每一个x∈S都有(x,x)∉R，则称R具有反自反性

• 对称性（symmetric）：如果对于任意(x,y)∈R，都有 (y,x)∈R，则称R具有对称性

• 反对称性（antisymmetric）: 如果对于任意(x,y)∈R(x≠y)，都有(y,x)∉R，则称R具有反对称性

• 传递性（transitive）: 如果对于任意(x,y)∈R,(y,z)∈R，都有(x,z)∈R，则称R具有传递性

有了这些属性定义，偏序就是满足自反性、反对称性和传递性的关系。定义在全集S上的偏序关系<，可以记作：L(S,<)。

直观的理解，偏序关系也就是定义了全集中部分元素间的相互可比较性。

全序

全序（total order）的本质就是一个偏序，什么样的偏序呢？如果偏序L(S,<)满足：对于任意的x∈S，y∈S，都满足要么(x,y)∈<，要么(y,x)∈<，两者必有其一，那么偏序<就是一个全序。

直观的理解，全序关系就是对全集中所有元素的相互可比较性定义。

为简便起见，偏序（或全序）L(S,<)可以简写为L，符号L既可以代表全集S又可以代表偏序（或全序）关系<，并且L和<可以互换使用。

0.3 偏序的约束与前缀

偏序的约束

偏序L(∑,<)的约束(restriction)也是一个偏序L′(∑′,<′)，且满足：

• ∑′⊆∑

• 对于任意的a,b∈∑，a<′b⇔a<b

偏序的前缀

偏序L(∑,<)的前缀（prefix）是一种特殊的约束L′(∑′,<′)，对于任意的a∈∑′，a在L中的所有前序（predecessors，所有∑中的元素b，满足b<a）也都在∑′中。

1. 事务

1.1 什么是事务

事务就是一个有限的数据操作序列。这些操作最终都会转换成具体数据项（data item）上的读或者写操作。除了读写操作，在事务执行的最后还会有一个提交(commit)或回滚(abort)操作，来表示事务最终执行完成，或者是执行失败。

这里用到了数据项的概念，数据项是数据库中保存数据的元素。明确的说明一下，数据项可以有各种不同的粒度，例如一个字段、一条记录、若果条记录组成的集合、一张表等等。没有明确说明时，数据项可以指任意粒度的数据项。

工欲善其事，必先利其器，下面严格的定义一下事务：某个事务Ti，是操作集合∑i上的一个全序关系Ti(∑i,<i)。其中，操作集合给出了事务中具体执行了哪些操作，所有操作可以分为下列四种类型：

1. 事务i对某个数据项x进行读操作，记作ri(x)

2. 事务i对某个数据项x进行写操作，也包括删除操作，记作wi(x)

3. 事务i执行提交操作，记作ci

4. 事务i执行回滚操作，记作ai

一个事务中，提交和回滚两个操作有且只有一个也就是说：ai∈∑i⇔ci∉∑i。并且，提交或回滚操作一定是事务的最后一个操作。

关系<i界定了事务中操作间的先后关系。例如事务Ti首先执行了对数据项x的读操作，然后执行了对数据项y的写操作，最后执行了提交操作，可以表示为：ri(x)<iwi(y)<ici。<i是全序关系，意味着，对于任意两个操作p,q∈∑i，要么p<_iq，要么q<_ip，两者必有其一。

1.2 顺序执行与并发执行

前面讲了这么多数据并发操作的问题，为了能够准确无误的讨论如何进行并发控制，有必要来明确说明一下事务或者是操作顺序执行、并发执行的概念：

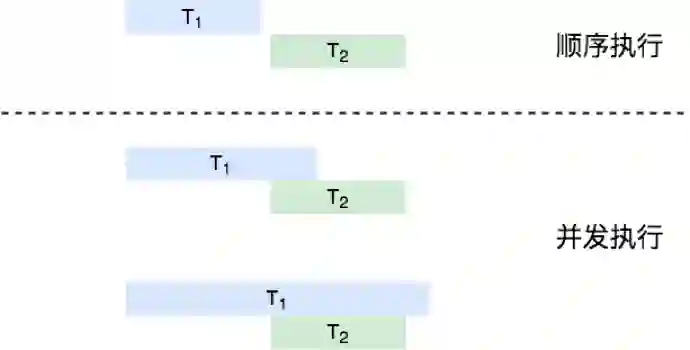
如果一个操作在另一个操作执行完成之后，再开始执行，则定义这两个操作是顺序执行，否则这两个操作就属于并发执行。同理，如果一个事务T在另一个事务 T′执行完成之后，再开始执行，则定义这两个事务是顺序执行，执行顺序为T′→T。否则这两个事务就属于并发执行。直观的，顺序执行与并发执行的概念可以用下图表示：

 

当存在事务的并发执行时，就会存在我们前面所讨论的数据并发访问问题。显然的，有下面这么一个结论：

公理1:如果所有事务都是顺序执行，那么事务中的所有操作也将顺序执行，就不会出现数据并发访问的问题。

这是并发控制理论的一个最基础的观察，是并发控制理论的基石性公理。

1.3 冲突操作

如果有两个事务，虽然是并发执行，但是它们访问的数据集完全没有交集，例如访问两个完全独立的库，各玩各的数据，那也不会发生数据并发访问问题，这很容易理解。

两个事务只有存在冲突操作（conflict operation）的时候，才会出现并发访问数据的问题。什么叫冲突操作？直观的讲，如果两个操作的计算效果（computational effect）与它们的相对执行顺序有关，则定义这两个操作为冲突操作。反之，如果计算效果与它们的相对执行顺序无关，否则它们就不是冲突操作。如何定义计算效果？由两部分组成：

1. 两个操作所取得的返回值（如果操作有返回值的话，没有则不计）

2. 这两个操作所涉及的所有数据项（0个或多个）的最终值

这两部分计算效果中的任意一部分因为两个操作的相对执行顺序不同而不同，就定义这两个操作为冲突操作。

关于冲突操作的判定有下面这个重要定理：

定理1：两个操作为冲突操作的充分必要条件是，这两个操作访问的数据项有交集，并且这两个操作中至少有一个是写操作。

根据冲突操作的定义，这个定理的成立是非常直观的，同时又为判断两个操作是否为冲突操作提供了便于操作方法。

2. 事务的调度

2.1调度器模型

数据库为用户提供了事务的概念，并以事务为单元，提供并发访问数据的保护。数据库可以用多种不同的算法对并发的数据访问进行保护，诸如两阶段锁，多版本并发控制，乐观的并发控制等等，这些具体的实现算法和在分布式环境下的新挑战，可扩展性的新需求，将在后面用系列小文章进行逐一讨论。本文把所有的这些算法，用统一的调度器模型来描述：事务的所有操作都需要依次提交到称作调度器（scheduler）的逻辑模块来调度执行。调度器在收到事务提交的操作后，可以有3种调度策略可选：

1. 立即执行：立即访问数据项，执行响应的操作并返回结果。事务在收到调度器的操作执行结果后，再继续执行下一个操作，直到完成；

2. 拒绝执行：调度器向事务返回拒绝执行，事务收到拒绝执行后将进入回滚操作；

3. 延迟执行：调度器在内部对事务提交的操作进行排队，延迟执行。操作的排队过程对事务透明，最终排队延迟执行的操作将出队，被立即执行，或者被拒绝执行。

绝大多数情况下，调度器的执行按照‘增量调度’的模式进行：调度器仅仅知道事务所有已经提交的操作，并据此进行调度，无法获得将来会执行何种操作的任何信息。也有一些调度算法，要求事先知道事务将来执行操作的某些信息，如在事务开始前就提供事务所有要读取的数据项集合（read set）和所有将修改的数据项集合（write set），并根据这些信息进行优化调度。不过在很多数据库提供的用户体验模式下，这种信息是无法获得的。后面在没有特别说明情况下，都假设调度器按照“增量调度”的模式进行。

2.2 事务的执行历史

调度器调度所有事务操作执行的结果，称作操作执行的历史(history)。直观的说，执行历史给出了事务集合中的所有操作，最终按照什么顺序执行的，是调度器工作的结果。在执行历史中，原有事务内的操作相对顺序将不变。事务之间的冲突操作，在执行历史中会给出明确的顺序关系。

下面准确的定义一下操作执行历史的概念。首先定义事务操作的完整执行历史（complete history），一个事务集合T=(T1,T2...Tn)的完整执行历史定义为一个偏序<H，满足：

1. 完整执行历史的操作全集是所有事务操作全集的并集，即：H=T1∪T2∪Tn

2. 每个事务中的全序关系在完整执行历史的偏序关系中依然成立，也就是说每个事务中各个操作的执行顺序在完整历史中依然保持，即：<H⊇(<1∪<2...<n)。

3. 对于所有有冲突的操作，完整执行历史的偏序关系，对其执行顺序有明确确定。即，对于H中任意两个有冲突的操作p和q，要么满足p<Hq，要么满足q<Hp，两者必有其一。

值得注意的的是在每个事务内部所有操作间是全序关系，在调度器调度时，事务操作的完整执行历史是一个偏序关系，也就是说不同事务间的操作，只要不是冲突操作，可以调度为并发执行。

有了操作的完整执行历史的准确定义后，操作执行历史的准确定义为：一个事务集合T=(T1,T2...Tn)的执行历史，是其完整执行历史的一个偏序前缀。直观的理解，操作执行历史是完整执行历史执行过程中的一个中间状态。完整执行历史表示了所有事务全部执行完成的全过程,执行历史则可以表示完整执行历史执行过程中的某个状态。

举个栗子，有三个事务：

• T1=r1(x)→w1(x)→c1

• T2=r2(x)→w2(y)→w2(x)→c2

• T3=r3(y)→w3(x)→w3(y)→w3(z)→c3

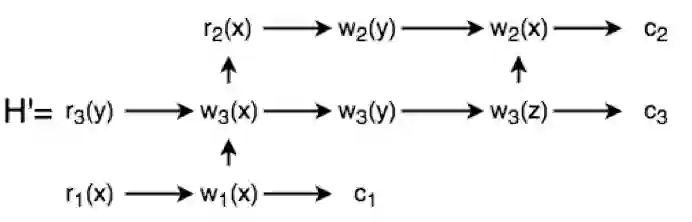
则这3个事务的一个完整执行历史可以是：

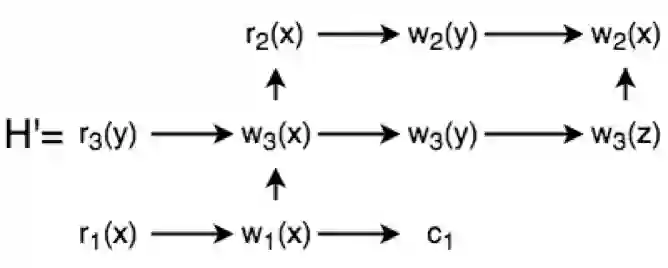
这个完整执行历史执行过程中的一个执行历史可以是：

3. 可串行化

用户通过数据库访问数据，希望得到的体验是：

• 功能上：对数据的访问尽量简单，每个事务在执行时能够像独占数据使用一样

• 性能上：能够获得越高的并行度越好，尽可能多的操作可以同时执行，充分利用系统资源

事务所有的操作都提交到调度器调度执行，要达到上述目标的关键就在于如何设计调度算法。显然的，如果调度器把所有事务都串行执行，则能满足上述的功能上的要求，但是性能上的要求就满足不了，完全串行的调度器，会浪费大量的系统资源。于是我们就需要有“可串行化”的调度器，也就是说并行事务的执行结果和把这些事务串行执行一样，但是期间可以并行的操作将会被挖掘出来，尽量的并行执行，充分利用系统资源，提高数据库的性能。

可串行化的调度算法有多种实现，这篇文章的目标是给出可串行调度算法实现的理论基础。接下去按照下面的路线图进行推导：

• 首先给出串行的完整执行历史的定义；

• 接着推导出执行历史等价的条件；

• 然后根据执行历史等价的条件定义可串行的执行历史（即与某个串行执行历史等价的历史）；

• 最后给出可串行化定理，是众多可串行调度算法设计与实现的基础。

3.1 串行的完整执行历史

一个完整执行历史H，如果对于其中的任意两个事务Ti和Tj，都满足，要么事务Ti中的所有操作都在Tj的操作之前，要么事务Tj中的所有操作都在事务Ti的所有操作之前，两者必有其一，那么就称H是一个串行的完整执行历史。

3.2 等价的执行历史

如果两个执行历史H和H'满足：

1. 两个历史中包含的事务集合和操作集合完全相同

2. 所有提交事务间的冲突操作，在两个历史中的相对执行顺序都相同。也就是说，对于任意的两个冲突操作p和q，假设它们所属的事务最终都是提交的，则若p<Hq，则必有p<H′q

那么就定义这两个事务是等价（equivalent，也称冲突等价，conflict equivalent）的。不难理解，执行历史的计算效果只与冲突操作的相对执行顺序有关，没有冲突的操作，无论相对执行顺序怎样，都不会影响最终计算效果。

3.3 可串行化的执行历史

与某个串行完整执行历史等价的执行历史就是可串行化的完整执行历史，这样的完整执行历史计算效果与串行完整执行历史相同，但却不一定要真正串行执行所有的操作。

但仔细观察不难发现，串行完整执行历史的定义是针对完整执行历史的。我们不但希望调度器产生的完整执行历史是可串行化的，而且在达成完成执行历史的任意中间执行过程，也就是调度器产生的所有历史都是可串行化的。为此，我们需要借助执行历史的提交投影的概念：

执行历史的提交投影：把某个事务执行的历史H中，所有属于未提交事务（包括回滚，或者是执行为结束的事务）的操作去掉后，剩下的部分，就称作执行历史的提交投影（commited projection），记作C(H)。

准确的说，C(H)是H的一个偏序约束，H中所有提交的事务组成了C(H)的全集。

显然的，执行历史的提交投影是一个完整执行历史，借助提交投影的概念定义可串行化执行历史：

如果一个历史H的提交投影C(H)与某个串行的完整执行历史Hs等价，那么就称执行历史H为可串行化的。

至此，我们定义了可串行执行历史的概念，只要保证数据库调度器调度产生的所有执行历史都是可串行化的，我们就能保证，在数据库执行过程中的任意时刻，事务执行的计算效果，都和事务集合的某种串行执行等价。用户在访问数据时可以像独占数据一样使用，并发执行的事务之间完全隔离。

这个定义从事务并发控制的最基础观察（串行事务一定没有数据并发访问问题）出发，一步步导出，是并发控制思想的最本质表达。下面将继续导出可串行化理论中的重要定理，它是众多可串行化调度算法的理论基础，直接指导了可串行调度算法的设计与实现。

3.4 可串行化定理

首先定义执行历史的可串行化图。执行历史H的可串行化图是一个有向图，H中的每个提交事务对应有向图中的一个节点。有向图中的所有边Ti→Tj(i≠j)都满足：至少存在一个Ti中的操作pi，与Tj中的操作qj冲突，并且pi<Hqj。

可串行化定理：执行历史H可串行化与SG(H)SG(H)无环等价。

这条定理是众多可串行调度算法的基础，证明比较直观，下面用一个例子来看一下这条定理的运用。

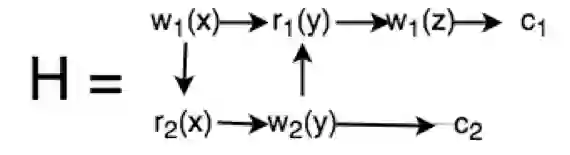
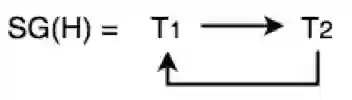
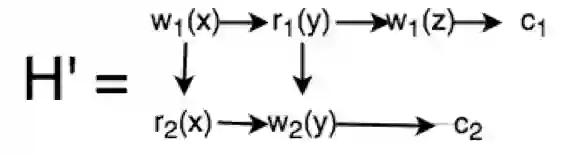
两个事务T1,T2的执行历史如下：

 

那么做出这个执行历史的可串行化图如下，有一个环，分析也不能发现，这个调度历史不是可串行化的历史。

如果把执行历史H稍加改动如下：

 

则这个执行历史就是可串行化的，做出它的可串行化图也没有环：

 

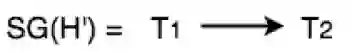
4. 小结

这篇文章以近期的一则新闻和一篇paper为背景，分析了只有完美的可串行级别事务隔离才能保证数据库数据的绝对正确，避免数据并发访问造成的问题与隐秘的Bug。并且这一特性在云数据库的商业模式和高并发的场景下显得越来越重要。在这一观察的基础上，为读者总结了可串行隔离的核心理论基础。从并发控制理论的最基础公理（完全串行执行就没有并发问题）出发，步步推导出了可串行化定理。