想研究前馈神经网络？先了解好它背后的数学吧！

作者 | Pranjut Gogoi

编译 | 聂震坤

如果你刚开始学习前馈神经网络，先了解其背后的数学原理则可以让以后事半功倍。

本文中笔者将在实践中深度探讨人工智能神经网络（ANN）技术。通常为了解决以一个问题，ANN 会拥有不同的层次，关于需要多少分层来解决一个特定问题则是另一个话题，将不在本篇中赘述。

作为一个程序员，应该比任何人都要更了解代码，无论看到什么样的代码都应该可以快速做出反应。因此，程序员可以直接从代码中来学习 ANN。然而，在开始了解 ANN 算法之前，了解算法背后的数学可以加快理解的速度。所以，在看代码之前，先关注代码背后的数学。尽管 ANN 有多种架构，我们先从下图的这一种前馈神经网络开始。

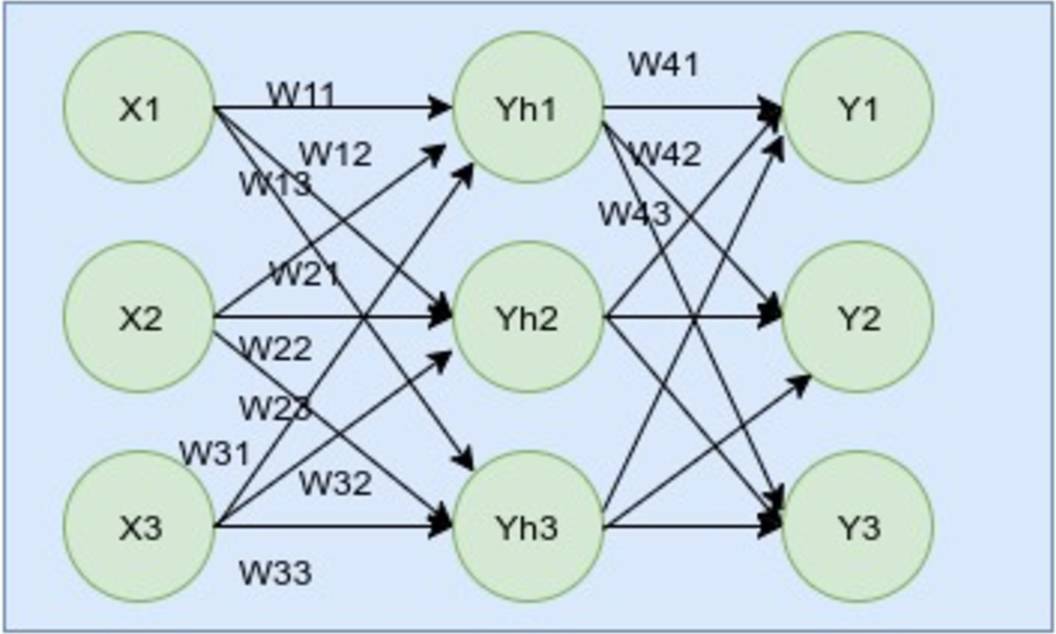
如图不难看出，此网络有3层：输入层，隐藏层，输出层。在输入层，我们有输入 X1, X2, …. Xn. 在中间和隐藏层我们有他的输出 Y1, Y2, Y3。我们将输出目标作为 , , …。同理，不同的神经元具有不同的比重，我们可以并将其命名为 X11 至 Yh1 之间的 W11；X1 至 Yh2 之间的 W12；X1 至 Yh3 之间的 W13，以此类推。我们也为输出层神经元做了类似的工作。这里要注意的一个重要事情是，ANN 是基于实值，离散值和向量值输入的。

下表是对上述内容的简单总结。如果你是新手，则强烈建议你看完他们。

• Inputs = X1, X2, X3

• Hidden outputs = Yh1, Yh2, Yh3

• Putputs = Y1, Y2, Y3

• Targeted outputs = Ŷ1, Ŷ2, Ŷ3

• Weights to Yh1 = W11, W12, W13

• Weights to Yh2 = W21, W22, W23

• Weights to Yh3 = W31, W32, W33

• Weights to Y1 = W41, W42, W43

• Weights to Y2 = W51, W52, W53

• Weights to Y3 = W61, W62, W63

现在，我们的准备工作已经完成，可以开始应用在神经网络上了。每一个神经元都有自己的激活方程，比如 f(x)=sigmoid(x)。激活方程将需要一个参数。我们的第一步便是为这个激活方程创建一个输入，通过将比重乘输入值来实现。公式如下：

• XWh1 = X1.W11 + X2. W21 + X3. W31

• XWh2 = X1.W12 + X2. W22 + X3. W32

• XWh3 = X1.W13 + X2. W23 + X3. W33

隐藏层的输出则为：

• Yh1 = sigmoid(XWh1)

• Yh2 = sigmoid(XWh2)

• Yh3 = sigmoid(XWh3)

隐藏层的输出值变成了输出层的输入值，并且与刚刚一样乘以比重。因此，过程应该如下：

• YhWo1= Yh1.W41+Yh2.W51+Yh3.W61

• YhWo2= Yh1.W42+Yh2.W52+Yh3.W62

• YhWo3= Yh1.W43+Yh2.W53+Yh3.W63

输出层的最终输出结果为：

• Y1 = sigmoid(YhWo1)

• Y2 = sigmoid(YhWo2)

• Y3 = sigmoid(YhWo3)

如果你刚开始学习神经网络，并且不了解什么是 Sigmoid 方程。下面附上其公式：

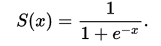
我们可以用 ANN 的各种激活方程来解决不同的问题。但简而言之， Sigmoid 函数在放在图上时会产生 S 形曲线。当神经网络的输入值是实值并可微分时，我们使用 Sigmoid 方程，因为我们可以很容易的找到他的梯度。

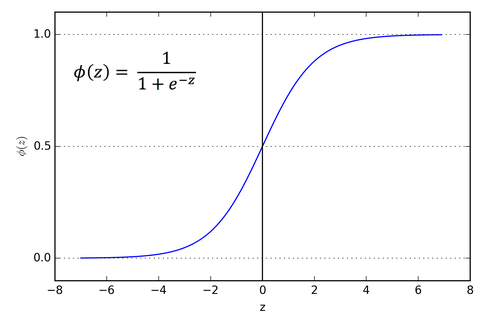
如果应用上文中所涉及的知识点，那么神经网络则应该已经准备就绪了。

原文：Learn the Math for Feedforward Neural Networks 

审校：屠敏 

---

7月22-23日，本年度中国人工智能技术会议最强音——2017 中国人工智能大会（CCAI 2017）即将在杭州国际会议中心拉开序幕。汇集超过40位学术带头人、8场权威专家主题报告、4场开放式专题研讨会、超过2000位人工智能专业人士将参与本次会议.

目前，大会 8 折优惠门票正在火热发售中，扫描下方二维码或点击【阅读原文】火速抢票。