小议 bootstrap （上）

当我们想从一个 sample 去推测 population 的某些参数时候，比如 population mean，我们可以用 sample mean 来作为 estimator，不论 population 的概率分布是什么样的都可以这样做。

那么，由于 sample 的随机性，显然 sample mean 会随着 sample 的不同而变化，也就是说 sample mean 本身就是一个随机变量。我们想知道这个随机变量的 variance，或者 confidence interval，怎么来求呢？

当然，如果 population 本身是 normal 分布的，那么 sample mean 也自然是 normal 分布的 (准确地说是 t distribution)。它的 variance 和 confidence interval 都可以通过 sample 自身的 variance 和 z-score 来估算，事情变得简单了许多。

但是，对于大部分非 normal distribution 的情况来说，想求得一个解析式是极其困难的。Bootstrapping 就是一个非常好的解决方法。

举个非常简单的例子，从一个任意分布的 population 中抽取 samples，设为 X1, X2, …, Xn，那么 sample mean 为 X.mean = (X1 + X2 + … + Xn) / n。假设 population mean 为 u，u 的 point estimate 为 X.mean，下面我们来讲怎么利用 bootstrapping 方法来计算 mean 的 90% confidence interval。

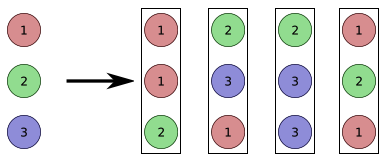
第一步，从这个 sample 中做 random sampling with replacement (每次抽取都是以原来那 n 个 data 为基准，所以每次抽取不影响后面的 sampling)。我们从中抽取 n 个 data（很多 data 会被重复抽取到），这 n 个新的 data 组成一个 bootstrap，计算它的 mean 为 Y.mean。

第二步，重复第一步，做很多次 bootstrapping（比如1000次），每次的 mean 为 Y1.mean, Y2.mean, …, Y1000.mean。

第三步，利用 Y1.mean, Y2.mean, …, Y1000.mean 来计算 X.mean 的 confidence interval。

至于怎样求 confidence interval，一个最简单的方法就是利用 Y.mean 的 empirical distribution (实际数据的分布) 来近似 x.mean 的 distribution，这个 empirical distribution 的 5% 到 95% 区间便是 u 的 90% confidence interval。

很多人都会按照上述方法来计算 confidence interval。在这里大家需要清楚一点，这个方法虽然简单，但同时也是最不准确的方法。

它需要很强的假设条件。第一，x.mean 的值需要离真实的 mean 也就是说 u 的值很近，往往 sample size 足够大的时候才可能满足该条件，具体需要多大的 size 也要取决于原来 population 的概率分布。第二，Y.mean 的概率分布需要和 X.mean 的真实分布很相近。第二点假设在很多情况下并不成立，比如最起码的一个要求就是 estimator 不能有任何 bias。

其实，bootstrapping 的理论并不简单，只不过直观上很好理解，而且实现起来特别容易。在下面一期，我们会讲到怎样用别的方式更准确地计算 confidence interval，其实也不难。

---

DeepLearning中文论坛公众号的原创文章，欢迎转发；如需转载，请注明出处。谢谢！

长按二维码，轻松关注数据科学文章