一文看懂线性回归（3个优缺点+8种方法评测）

线性回归是很基础的机器学习算法，本文将通俗易懂的介绍线性回归的基本概念，优缺点，8 种方法的速度评测，还有和逻辑回归的比较。

什么是线性回归？

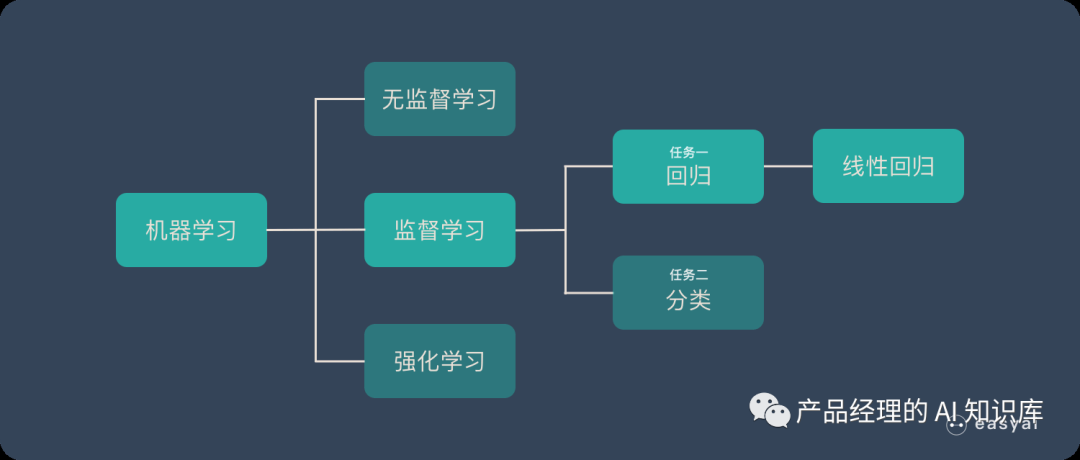
线性回归的位置如上图所示，它属于机器学习 - 监督学习 - 回归 - 线性回归。

扩展阅读：

《机器学习》

《监督学习》

什么是回归？

回归的目的是为了预测，比如预测明天的天气温度，预测股票的走势…

回归之所以能预测是因为他通过历史数据，摸透了“套路”，然后通过这个套路来预测未来的结果。

什么是线性？

“越…，越…”符合这种说法的就可能是线性个关系：

「房子」越大，「租金」就越高

「汉堡」买的越多，花的「钱」就越多

杯子里的「水」越多，「重量」就越大

……

但是并非所有“越…，越…”都是线性的，比如“充电越久，电量越高”，他就类似下面的非线性曲线：

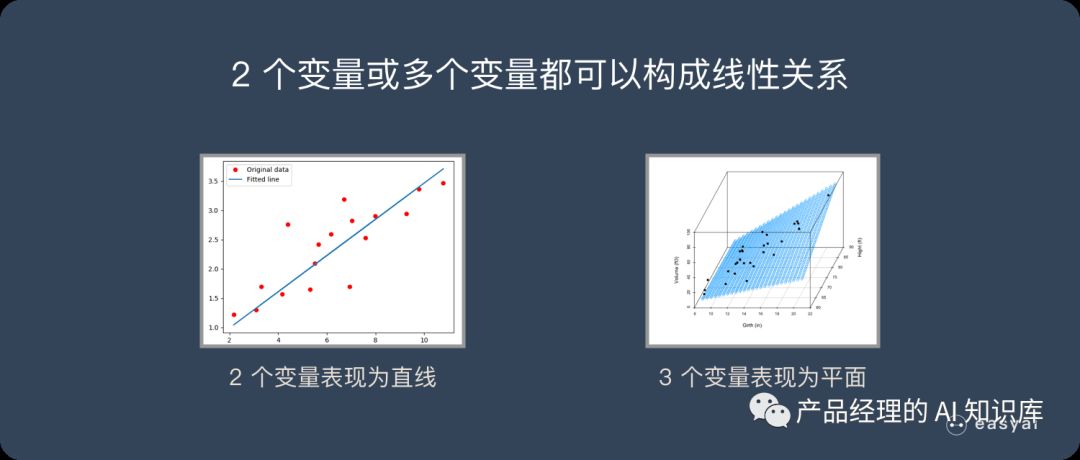
线性关系不仅仅只能存在 2 个变量（二维平面）。3 个变量时（三维空间），线性关系就是一个平面，4 个变量时（四维空间），线性关系就是一个体。以此类推…

什么是线性回归？

线性回归本来是是统计学里的概念，现在经常被用在机器学习中。

如果 2 个或者多个变量之间存在“线性关系”，那么我们就可以通过历史数据，摸清变量之间的“套路”，建立一个有效的模型，来预测未来的变量结果。

线性回归的优缺点

优点：

1. 建模速度快，不需要很复杂的计算，在数据量大的情况下依然运行速度很快。

2. 可以根据系数给出每个变量的理解和解释

缺点：不能很好地拟合非线性数据。所以需要先判断变量之间是否是线性关系。

为什么在深度学习大杀四方的今天还使用线性回归呢？

一方面，线性回归所能够模拟的关系其实远不止线性关系。线性回归中的“线性”指的是系数的线性，而通过对特征的非线性变换，以及广义线性模型的推广，输出和特征之间的函数关系可以是高度非线性的。另一方面，也是更为重要的一点，线性模型的易解释性使得它在物理学、经济学、商学等领域中占据了难以取代的地位。

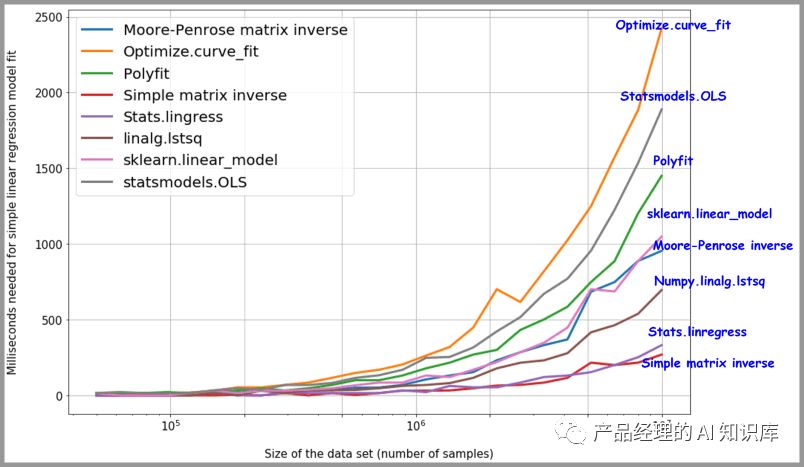
8 种Python线性回归的方法的速度评测

1. Scipy.polyfit( ) or numpy.polyfit( )

2. Stats.linregress( )

3. Optimize.curve_fit( )

4. numpy.linalg.lstsq

5. Statsmodels.OLS ( )

6. 简单的乘法求矩阵的逆

7. 首先计算x的Moore-Penrose广义伪逆矩阵，然后与y取点积

8. sklearn.linear_model.LinearRegression( )

结果：令人惊讶的是，与广泛被使用的scikit-learnlinear_model相比，简单矩阵的逆求解的方案反而更加快速。

详细评测可以查看原文《Data science with Python: 8 ways to do linear regression and measure their speed》

https://www.freecodecamp.org/news/data-science-with-python-8-ways-to-do-linear-regression-and-measure-their-speed-b5577d75f8b/

线性回归 VS 逻辑回归

线性回归和逻辑回归是 2 种经典的算法。经常被拿来做比较，下面整理了一些两者的区别：

1. 线性回归只能用于回归问题，逻辑回归虽然名字叫回归，但是更多用于分类问题（关于回归和分类的区别可以看看这篇文章《监督学习》）

2. 线性回归要求因变量是连续性数值变量，而逻辑回归要求因变量是离散的变量

3. 线性回归要求自变量和因变量呈线性关系，而逻辑回归不要求自变量和因变量呈线性关系

4. 线性回归可以直观的表达自变量和因变量之间的关系，逻辑回归则无法表达变量之间的关系

注：

自变量：主动操作的变量，可以看做「因变量」的原因

因变量：因为「自变量」的变化而变化，可以看做「自变量」的结果。也是我们想要预测的结果。

---