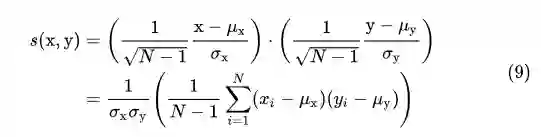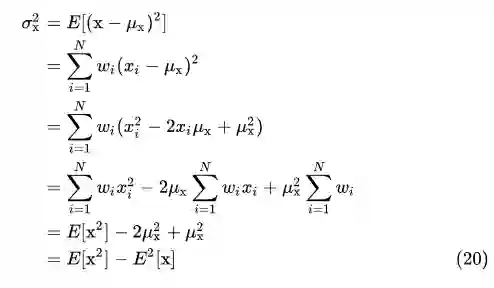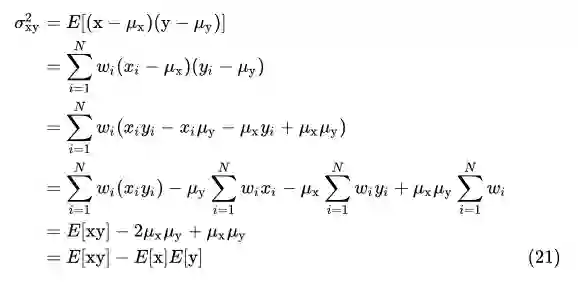源码解析 | 图像质量损失函数SSIM Loss的原理详解和代码具体实现

2019 年 6 月 2 日 人工智能前沿讲习班

首先，本文解读一篇2004年的文献：Image Quality Assessment: From Error Visibility to Structural Similarity 。该文献提出了一种衡量重建图像和原图的相似性的metric：Structural Similarity (SSIM)，这个 metric 被广泛采纳，至今已经有两万多引用量了。然后，本文将提炼论文内容，结合 skimage 下的代码讲解 SSIM metric 的具体实现，并给出 SSIM Loss在pytorch下的代码链接。

作者：SIGAI人工智能平台

出处：SIGAI人工智能平台

公众号：SIGAI

背景

在图像重建、压缩领域，有很多算法可以计算输出图像与原图的差距，其中最常用的一种是 Mean Square Error loss（MSE）。它的计算公式很简单：

就是 element-wise 地计算重建图像与输入图像的像素差的平方，然后在全图上求平均。

但作者认为，传统基于 MSE 的损失不足以表达人的视觉系统对图片的直观感受。例如有时候两张图片只是亮度不同，但是之间的 MSE loss 相差很大。而一幅很模糊与另一幅很清晰的图，它们的 MSE loss 可能反而相差很小。下面举个小例子：

import cv2import numpy as npimport matplotlib.pyplot as plt
origin = cv2.imread('c.png', 0)dark = (origin*0.9).astype('uint8')blur = cv2.GaussianBlur(origin, (5,5), 0)
mse_dark = np.mean((origin-dark)**2)mse_blur = np.mean((origin-blur)**2)
fig, axes = plt.subplots(1, 3)axes[0].imshow(origin, 'gray')axes[0].title.set_text('origin')axes[0].axis('off')
axes[1].imshow(dark, 'gray')axes[1].title.set_text('0.9 dark mse: {:.2f}'.format(mse_dark))axes[1].axis('off')
axes[2].imshow(blur, 'gray')axes[2].title.set_text('blur mse: {:.2f}'.format(mse_blur))axes[2].axis('off')
plt.show()
print('MSE dark : {}'.format(mse_dark))print('MSE blur : {}'.format(mse_blur))

从图中可以看出 MSE 反映的距离和我们人类的直观感受有很大区别

上图左侧为原图，中间为把灰度值调整为原来 0.9 的图，右侧为高斯模糊后的图。我们人眼明显感觉到中间的图比右边的图清晰，然而 MSE 距离显示，右侧的图与原图的距离远小于中间的图与原图的距离，即右侧的图质量比中间的高。

作者结合神经科学的研究，认为我们人类衡量两幅图的距离时，更偏重于两图的结构相似性，而不是逐像素计算两图的差异。因此作者提出了基于 structural similarity 的度量，声称其比 MSE 更能反映人类视觉系统对两幅图相似性的判断。

那么作者是怎么做的呢？

图像的 Structural Similarity

作者把两幅图 x, y 的相似性按三个维度进行比较：亮度（luminance）l(x,y)，对比度（contrast）c(x,y)，和结构（structure）s(x,y)。最终 x 和 y 的相似度为这三者的函数：

作者设计了三个公式定量计算这三者的相似性，公式的设计遵循三个原则：

对称性：
有界性：
极限值唯一：当且仅当 x = y

首先研究亮度。如果一幅图有 N 个像素点，每个像素点的像素值为，那么该图像的平均亮度为：

作者用如下公式衡量两幅图 x 和 y 的亮度相似度：

这里是为了防止分母为零的情况，且：

其中是一个常数，具体代码中的取值为 0.01，L 是灰度的动态范围，由图像的数据类型决定，如果数据为 uint8 型，则 L=255。可以看出，公式 (4) 对称且始终小于等于1，当 x = y 时为1。

接下来研究对比度。所谓对比度，就是图像明暗的变化剧烈程度，也就是像素值的标准差。其计算公式为：

对比度的相似度公式和公式 (4) 极为相似，只不过把均值换成了方差，作者定义：

其中：

一般在代码中取 0.03。公式 (7) 也对称且小于等于1，当 x = y 时等号成立。

最后研究结构相似度。需要注意的是，对一幅图而言，其亮度和对比度都是标量，而其结构显然无法用一个标量表示，而是应该用该图所有像素组成的向量来表示。同时，研究结构相似度时，应该排除亮度和对比度的影响，即排除均值和标准差的影响。归根结底，作者研究的是归一化的两个向量：和之间的关系。根据均值与标准差的关系，可知这两个向量的模长均为。因此它们的余弦相似度为：

上式中第二行括号内的部分为协方差公式：

同样为了防止分母为0，分子分母同时加：

结合 (4) (7) (11)，作者定义两图的相似度公式为:

令，的分子和的分母可以约分，最终得到 SSIM 的公式：

因此，可以结合公式 (3) (6) (10) (13) 计算两个向量 x，y 的 structural similarity，。

Mean Structural Similarity

然而，上面的 SSIM 不能用于一整幅图。因为在整幅图的跨度上，均值和方差往往变化剧烈；同时，图像上不同区块的失真程度也有可能不同，不能一概而论；此外类比人眼睛每次只能聚焦于一处的特点。作者采用 sliding window 以步长为 1 计算两幅图各个对应 sliding window 下的 patch 的 SSIM，然后取平均值作为两幅图整体的 SSIM，称为 Mean SSIM。简写为 MSSIM（注意和后续出现的 multi-scale SSIM：MS-SSIM 作区分）。

代码中，计算每个 patch 的均值和方差时，作者采用了方差为 1.5 的高斯卷积核作加权平均，滑窗大小为 11*11 。

如果像素对应的高斯核权重为。那么加权均值，方差，协方差的公式为：

假如整幅图有 M 个 patch，那么 MSSIM 公式为：

在具体研究代码之前，我们先调用一下 skimage.measure 下的 compare_ssim 看看 MSSIM 的效果是不是比 MSE 好。同样以开头的两图为例：

import cv2import numpy as npimport matplotlib.pyplot as pltfrom skimage.measure import compare_ssim
origin = cv2.imread('c.png', 0)dark = (origin*0.9).astype('uint8')blur = cv2.GaussianBlur(origin, (5,5), 0)
# mse_dark = np.mean((origin-dark)**2)# mse_blur = np.mean((origin-blur)**2)ssim_dark = compare_ssim(origin, dark)ssim_blur = compare_ssim(origin, blur)
fig, axes = plt.subplots(1, 3)axes[0].imshow(origin, 'gray')axes[0].title.set_text('origin')axes[0].axis('off')
axes[1].imshow(dark, 'gray')axes[1].title.set_text('0.9 dark ssim: {:.2f}'.format(ssim_dark))axes[1].axis('off')
axes[2].imshow(blur, 'gray')axes[2].title.set_text('blur ssim: {:.2f}'.format(ssim_blur))axes[2].axis('off')
plt.show()
print('SSIM dark : {}'.format(ssim_dark))print('SSIM blur : {}'.format(ssim_blur))

运行结果如下图所示：

中间单纯调节亮度的图片和原图的相似性大于高斯模糊后的图，符合人类的感受

我们发现单纯调节亮度后，中间的图和原图的相似度仍然是 0.99 ，而高斯模糊后的图，和原图的相似性只有 0.85，果然 MSSIM 比 MSE 效果要好。

skimage 代码实现

详细代码请直接看 skimage 的源码，这里限于篇幅只复制粘贴本人认为重要的部分。此外由于 pytorch 自带的自动求导机制，我们不必手推求导公式，本文将忽略 skimage 代码中 MSSIM 对输入图像求梯度的部分。感兴趣的可以参考 skimage 给出的文献[2]：Avanaki, A. N. (2009). Exact global histogram specification optimized for structural similarity.

import numpy as npfrom scipy.ndimage import uniform_filter, gaussian_filter
from skimage.util.dtype import dtype_rangefrom skimage.util.arraypad import crop

def compare_ssim(X, Y, win_size=None,                 dynamic_range=None,                 gaussian_weights=False, full=False, **kwargs):
    # 下面三个参数都是原始论文中给定的    K1 = 0.01    K2 = 0.03    sigma = 1.5
    # 计算方差和协方差时，采用无偏估计（除以 N-1）    # 数学上虽然好看，但其实影响不大    use_sample_covariance = True
    if win_size is None:        # 两种计算均值的方式，第一种是计算高斯加权后的均值和方差、协方差        # 第二种是直接计算这三个统计量        # 两种方式对应的滑窗尺寸不同        if gaussian_weights:            win_size = 11  # 11 to match Wang et. al. 2004        else:            win_size = 7   # backwards compatibility
    if not (win_size % 2 == 1):        # 滑窗边长必须是奇数，保证有中心像素        raise ValueError('Window size must be odd.')
    if dynamic_range is None:        # 根据图像数据类型确定动态范围        # 如果是 uint8 型则为 0 到 255        # 如果是 float 型则为 -1 到 1        dmin, dmax = dtype_range[X.dtype.type]        dynamic_range = dmax - dmin
    # 灰度图像为 2，彩色图像为3，    # 但计算彩色图像的 MSSIM 时，其实是把它分解为各个通道的灰度图像分别计算，然后再求平均    ndim = X.ndim
    # 确定到底采用哪种类型的滑窗    if gaussian_weights:        # sigma = 1.5 to approximately match filter in Wang et. al. 2004        # this ends up giving a 13-tap rather than 11-tap Gaussian        filter_func = gaussian_filter        filter_args = {'sigma': sigma}
    else:        filter_func = uniform_filter        filter_args = {'size': win_size}
    # ndimage filters need floating point data    # 把 uint8 型数据转为 float 型    X = X.astype(np.float64)    Y = Y.astype(np.float64)        # 滑窗所覆盖的像素点的个数    NP = win_size ** ndim
    # filter has already normalized by NP    if use_sample_covariance:        # filter 函数求的是在 NP 个点上的平均        # 现在想要无偏估计，则需要乘以 NP 再重新除以 NP-1        cov_norm = NP / (NP - 1)  # sample covariance    else:        cov_norm = 1.0  # population covariance to match Wang et. al. 2004
    # compute (weighted) means    # 计算两幅图的平均图，ux，uy 的每个像素代表以它为中心的滑窗下所有像素的均值(加权) E(X), E(Y)    ux = filter_func(X, **filter_args)    uy = filter_func(Y, **filter_args)
    # compute (weighted) variances and covariances    # 计算 E(X^2), E(Y^2)    uxx = filter_func(X * X, **filter_args)    uyy = filter_func(Y * Y, **filter_args)    # 计算 E(XY)    uxy = filter_func(X * Y, **filter_args)    # sigma_x^2 = E(x^2)-E(x)^2，下文会给出推导    vx = cov_norm * (uxx - ux * ux)    # sigma_y^2 = E(y^2)-E(y)^2    vy = cov_norm * (uyy - uy * uy)    # cov(x,y) = E(xy)-E(x)E(y)，下文会给出推导    vxy = cov_norm * (uxy - ux * uy)
    R = dynamic_range    # paper 中的公式    C1 = (K1 * R) ** 2    C2 = (K2 * R) ** 2        # paper 中的公式    A1, A2, B1, B2 = ((2 * ux * uy + C1,                       2 * vxy + C2,                       ux ** 2 + uy ** 2 + C1,                       vx + vy + C2))    D = B1 * B2    S = (A1 * A2) / D
    # to avoid edge effects will ignore filter radius strip around edges    # 截去边缘部分，因为卷积得到的边缘部分的均值并不准确，是靠扩充边缘像素的方式得到的。    pad = (win_size - 1) // 2
    # compute (weighted) mean of ssim    # 计算 SSIM 的均值    mssim = crop(S, pad).mean()
    if full:        return mssim, S    else:        return mssim

skimage 的源码十分简洁明了，唯一需要知道的数学公式大概是：

非加权平均包含在加权平均的情况之下，因此这里只推导加权的情况，若为权重，根据 (15)：

想求图像的方差，只需做两次卷积，一次是对原图卷积，一次是对原图的平方卷积，然后用后者减去前者的平方即可。

根据 (16)：

求两图的协方差，只需做三次卷积，第一次是对两图的乘积卷积，第二次和第三次分别对两图本身卷积，然后用第一次的卷积结果减去第二、三次卷积结果的乘积。

Pytorch 实现

下面的链接是计算 SSIM 的 pytorch 代码：https://github.com/Po-Hsun-Su/pytorch-ssim/blob/master/pytorch_ssim/__init__.py如果看懂了 skimage 的代码，相信你肯定也能理解这个代码。该代码只实现了高斯加权平均，没有实现普通平均，但后者也很少用到。

对比 SSIM 损失与 MSE 损失，SSIM 收敛更快，而且初期就能捕捉到图片的结构信息，随着迭代次数的增加，随机噪声很快消失了。而 MSE 只是单纯独立地优化每个像素点，导致即使到后期，画面上仍然出现很多噪点。

-----END-----