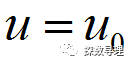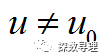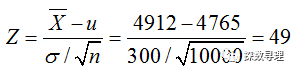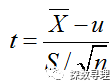如何通俗地理解假设检验基本原理
浩彬老撕,R语言中文社区特邀作者,好玩的IBM数据工程师,立志做数据科学界的段子手。
个人公众号:探数寻理
前文推送:
假设检验的基本原理
在日常的统计分析当中,我们针对所研究问题的全体对象,称之为总体。例如我们想要研究2017年大学生毕业生的薪酬水平,那么在2017年所有大学毕业生就是研究问题的总体。
但事实上,假如要研究这个问题,我们并不会对该年的所有应届毕业生进行问卷调查,因为数量实在太多了!
那怎么办?
一般情况下,我们可以从总体当中,按照一定的方法抽取部分的研究对象作为研究,而这部分的抽取对象,我们称之为样本。
事实上,由于总体分布未知,通过抽取样本数据进行测量,从而对总体作出理论的方法,我们称之为统计推断。假设检验是统计推断的重要组成内容。它是通过构造假设条件,并通过样本数据对假设条件进行检验,从而得出结论的方法。
例如,从过往的资料中,我们知道2016年大学毕业生平均薪酬为4765元,标准差为300元,现在从2017年的大学毕业生中随机抽取10000名,调查得到其平均薪酬为4912元,现在我们想知道2017年大学毕业生的平均薪酬和2016年相比是否有显著差异?
从抽样调查结果,我们知道17年的平均薪酬为4912元,相比于16年增加了147元,但现在问题在于这147元的差异可能有两种可能引起:第一种可能是,17年和16年的平均薪酬其实并没有太大差别,只是由于抽样误差引起了147元的波动;第二种可能是17年和16年的平均薪酬确实有明显差异,由于经济的增长,17年的平均薪酬确实增加了。
事实上,假设检验的核心正是判断这个差异是否足以通过抽样的随机性来解释。
因此,首先我们构造两个假设,第一个假设称之为原假设,也被称为H0,例如假定前后两个总体没有显著差异:
第二个假设称之为备设假设,也被称为H2,假定前后两个总体有显著差异,
之后,我们可则以构造一个与此相关的统计量,如果该统计量非常的大(即已经超过了一定的临界值),我们则可以认为这种差异并不仅仅是由抽样误差带来的,因此我们可以拒绝原假设,认为两个总体有显著差异。
值得注意的是,假设检验是一种“小概率反证”的思想。即原假设成立的前提下,小概率事件在一次试验中不太可能发生,如果发生了,则认为原假设并不成立。
在这里,小概率事件的阈值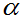
假设检验的一般步骤
我们继续以上一节中的大学毕业生工资水平变动情况的例子来说明假设检验的步骤。
1. 建立假设检验
零假设H0: 2017年大学毕业生平均工资与2016年大学毕业生平均工资无显著差异;
备设假设H1:2017年大学毕业生平均工资与2016年大学毕业生平均工资有显著差异;
设定显著性水平: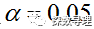
2. 选择假设检验方法和计算检验统计量
根据研究分析的目的和数据类型,确定检验方法。常用的检验方法包括Z检验,t检验,卡方检验等。
在本例中,我们属于单组样本检验,并已知总体均值和方差,因此可以常用Z检验。在原假设成立的前提下,可以采用如下Z统计量:
另外,在某些情况下,由于不知道总体方差,可以采用t检验代替:
(该检验统计量服从自由度n-1的t分布)
3. 判断临界值,作出结论
因为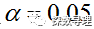
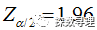

进一步来看,除了通过计算检验统计量是否超过临界值进行判断之外,还可以计算P值。P值的含义是,当原假设为真的情况下,根据样本所计算得到的检验统计量的结果或更极端结果的概率。因此可知,当P值小于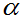
最好玩
最通俗
最易懂
de
机器学习课程
Now
限免
限免
限免
现在扫描下方二维码即可免费学习
点击阅读原文即可购买配套教材书籍