首次观测到超低温度下钠钾基态分子和钾原子碰撞的散射共振

2019 年 6 月 13 日 中国物理学会期刊网

作者：杨欢^1,2 赵博^1,2 潘建伟^1,2

(1 中国科学技术大学合肥微尺度物质科学国家研究中心

(2 量子信息与量子科技前沿协同创新中心)

量子计算和量子模拟具有强大的并行计算和模拟能力，不仅为经典计算机无法解决的大规模计算难题提供有效解决方案，也可有效揭示复杂系统的物理规律，为新能源开发、新材料设计等提供指导^[1]。量子计算研究的终极目标是构建通用型量子计算机，但这一目标需要制备大规模的量子纠缠并进行容错计算，实现这一目标仍然需要经过长期不懈的努力。当前，量子计算的短期目标是通过发展专用型量子计算机，即专用量子模拟机，能够在某些特定的问题上解决现有经典计算机无法解决的问题。例如，超冷原子分子量子模拟^[2，3]，利用高度可控的超冷量子系统来模拟复杂的难于计算的物理系统，可以对复杂系统进行细致和全方位的研究，从而在化学反应和新型材料设计中具有广泛的应用前景。

在化学物理领域，通过量子力学计算原子分子相互作用势能面以及模拟粒子在这一势能面下分子碰撞的动力学是一个重要科学问题^[4]。理论上计算原子分子的势能面需要求解多电子体系的薛定谔方程来得到电子系统的基态能量。由于电子之间存在强关联，其基态能量无法精确求解。因此理论量子化学发展各种方法来近似求解势能面，并在小质量少电子的分子体系取得了成功^[5—8]。但是对大质量多电子的分子体系，理论计算的势能面已经无法可靠地模拟分子碰撞中的动力学问题。

通过构建针对特定问题的专用量子模拟系统，势能面的信息可以由实验测量原子分子的散射共振来获得。散射共振的测量结合理论建模可以准确地反推出势能面的全局信息，从而给出势能面最精准的刻画^[9]。分子的散射共振是典型的量子现象，只有在超低温度下才会显现出来。近年来，随着超冷原子分子技术的发展，完全可控的超冷基态分子可以从接近绝对零度的原子气中被制备出来^[10—15]。但由于这种大质量多电子分子体系的散射共振无法在理论上进行预测，十余年来观测超冷分子的散射共振一直是该研究领域在实验上的重大挑战。

对于超低温度下分子的反应性碰撞，分子的化学反应速率仅仅决定于分子之间的长程相互作用。当进入短程相互作用区域时，分子会因为发生化学反应而立即损失，导致分子碰撞的散射共振完全被抑制^[16，17]。而对于超低温度下分子间的非反应性碰撞，由于分子相互作用势能面非常深，能够支持数目非常多的束缚态，导致在分子的入射能量附近束缚态密度可能非常高，散射共振能否分辨在理论上已经无法预测^[18]。尤其是在考虑核自旋和外加磁场的情况下，理论已经无法精确地给出分子碰撞的散射共振信息^[19]。在这种情况下，理论提出一个描述散射共振密度的统计模型^[18]，该模型预测温度在1 μK以下，分子和原子碰撞s 波散射共振平均间距将小于1 G，然而实验是否能够分辨散射共振仍然是未知的。

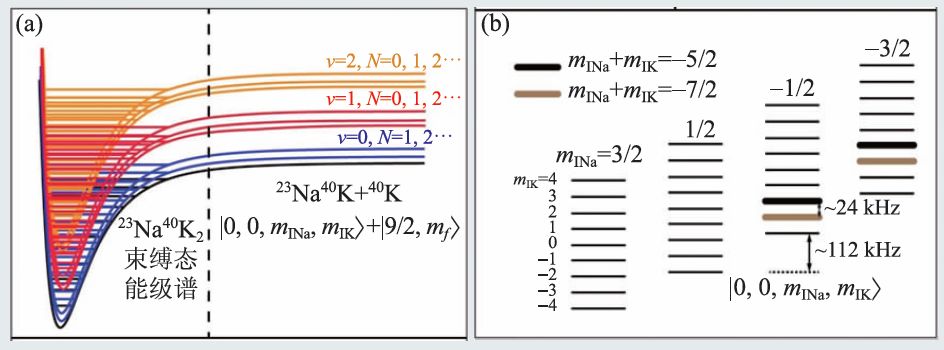
在实验中我们将超冷钠钾基态分子和钾原子混合气体作为研究对象。基态钠钾分子和基态钾分子束缚能分别为5212 cm^-1^[20]和4405 cm^-1^[21]，使得在超低温度下吸热反应²³Na⁴⁰K+⁴⁰K→⁴⁰K₂+²³Na由于能量不足而不会发生，超冷钠钾基态分子和钾原子混合气化学稳定。钾—钠—钾三原子相互作用势能曲面深度约为7125 cm^-1^[22]，能够支持非常多的三原子分子束缚态(图1(a))。实验通过调节磁场，可以对钠钾基态分子和钾原子散射态与钾—钠—钾三原子分子束缚态之间的能量差进行精确操控。同时基态钠钾分子和钾原子都是费米子，在超低温度下只会发生基态分子和原子间的两体碰撞，因此通过观测不同磁场下钠钾基态分子和钾原子之间的共振增强碰撞损失，可以观测分子和原子之间的散射共振。

图1 钠钾基态分子和钾原子散射示意图(a)钾—钠—钾三原子相互作用势能面能够支持非常多的三原子分子束缚态。当钠钾基态分子和钾原子入射能量与三原子束缚态能量接近时，将发生散射共振现象；(b)钠钾基态分子在100 G下的超精细能级结构。m_INa、m_IK分别代表钠、钾原子的核自旋投影。图中加粗标记的能级，为实验制备的基态分子量子态^[23]

我们的实验从温度约500 nK的钠、钾原子超冷混合气体出发，利用钠钾原子间Feshbach 共振，采用拉曼合成方法合成弱束缚钠钾Feshbach分子。合成钠钾Feshbach 分子后，立即将剩余在光阱中的钠原子选择性地移除，再利用绝热受激拉曼技术(STIRAP)将Feshbach 分子绝热转移至基态，从而制备出超低温度钠钾基态分子和钾原子混合气。由于Feshbach 分子合成效率约15%，导致钠钾基态分子和钾原子混合气中，基态分子数目比原子数目低约一个量级。实验通过测量不同磁场下钠钾基态分子寿命，则可以寻找钠钾基态分子和钾原子碰撞的散射共振。分子的内态可以用|v，N，m_INa，m_IK>表示，其中v，N分别表示分子振动和转动量子数，m_INa和m_IK分别表示钠原子和钾原子的核自旋量子数，当分子处于基态时，振动和转动量子数都为零。在我们的实验中，通过在受激拉曼过程选择不同的中间态，可以将分子制备在|0，0，-3/2， - 2> ， |0，0， - 3/2， -1> ，|0，0，－1/2， - 3> 和|0，0，- 1/2，-2> 态上( 图1(b))。同时，实验利用射频脉冲可以将钾原子制备在不同内态|F，m_F> = |9/2，m_f>，m_f= - 9/2，…，-1/2 。最终可以制备20 种钠钾基态分子和钾原子不同内态组合的超冷混合气体。

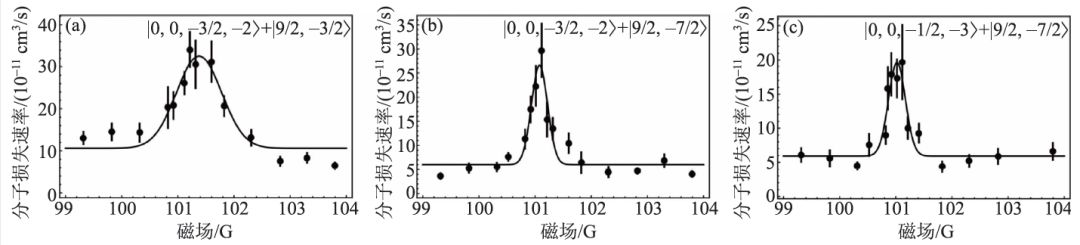
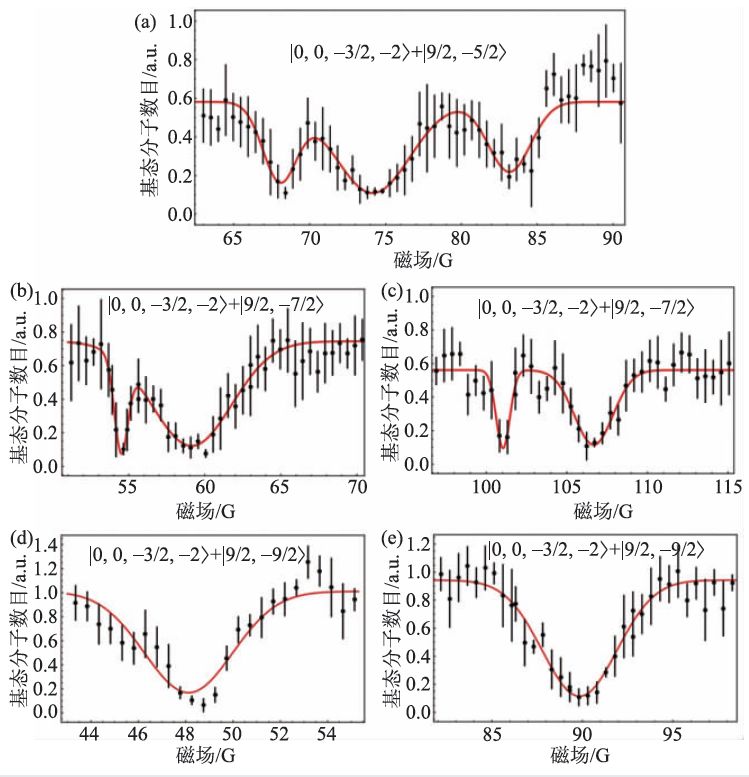
在实验中，钠钾基态分子制备和探测都需要在原子Feshbach 共振磁场附近完成。在该条件下，实验首先在钠钾原子Feshbach 共振磁场附近小范围磁场测量基态分子和原子的碰撞损失，并在101 G附近找到3 个基态分子的共振损失峰(图2)。为了能够扩大磁场测量范围，实验通过线圈电流补偿涡旋电流的方法，在制备钠钾基态分子和钾原子混合气后，快速地将磁场扫描至目标磁场。并将基态分子和钾原子混合气在目标磁场保持约7 ms，移除钾原子，再将磁场扫描回起始磁场，测量剩余的钠钾基态分子数量，寻找钠钾基态分子和钾原子碰撞的散射共振。利用这种方法，实验扫描了43—120 G磁场范围，并成功观测到9 个钠钾基态分子和钾原子的散射共振，如图3 所示。其中|0，0， - 3/2，-1> 态钠钾分子与|9/2， - 7/2>态钾原子混合体系在110 G的散射共振在两种方法中都被观测到，相互验证了两种方法的可靠性。综合两种实验方法，实验共观测了11 个钠钾基态分子和钾原子的散射共振。

图2 利用分子损失速率观测到的钠钾基态分子与钾原子碰撞的散射共振。通过测量钠钾基态分子在不同磁场下的损失速率，实验观测到(a)| 0，0，－3/2，－2> + |9/2，－3/2> 、(b) |0，0，－3/2，－2> + |9/2，－7/2> 和(c) |0，0，－1/2，－3> + |9/2，－7/2> 散射通道在101 G附近的散射共振^[23]

该工作最近在Science (《科学》)杂志上发表^[23]。分子的散射共振现象一直是超冷分子领域研究的重要问题，该工作首次在钠钾基态分子和钾原子超冷混合气中观测到散射共振现象。这些散射共振提供了对含有高达49 个电子的钾—钠—钾三原子分子复杂体系势能面的超高精度测量，成功获取了势能面在短程部分的重要信息，为实验研究和理解超低温度下分子的相互碰撞提供新的机遇。同时，超低温度下分子和原子之间的散射共振也许可以用来合成超冷三原子分子，为实验研究超低温度多原子分子开辟新的方向。

图3 通过扫描磁场测量的基态分子在不同磁场下的共振损失。扫描磁场，测量钠钾基态分子和钾原子在特定磁场保持相同时间后剩余的钠钾基态分子数目，寻找到的钠钾基态分子与钾原子间的散射共振。其中|0，0， - 3/2， - 2> + |9/2， - 7/2> 于101 G附近的散射共振在两种方法中都得到观测^[23]

参考文献

[1]Wilczek F. Physics Today，2016，69(4)：32

[2] Bloch I et al. Nature Physics，2012，8：267

[3] Cirac J I et al. Nature Physics，2012，8：264

[4] Herschbach D. Faraday Discussions，2009，142：9

[5] Qiu M et al. Science，2006，311：1440

[6] Vogels S N et al. Science，2015，350：787

[7] Chefdeville S et al. Science，2013，341：1094

[8] Yuan D F et al. Science，2018，362：1289

[9] Chin C et al. Rev. Mod. Phys.，2010，82：1225

[10] Ni K K et al. Science，2008，322：231

[11] Park JWet al. Phys. Rev. Lett.，2015，114：205302