中科院计算所沈华伟:图神经网络表达能力的回顾和前沿
作者 | 蒋宝尚
编辑 | 丛末

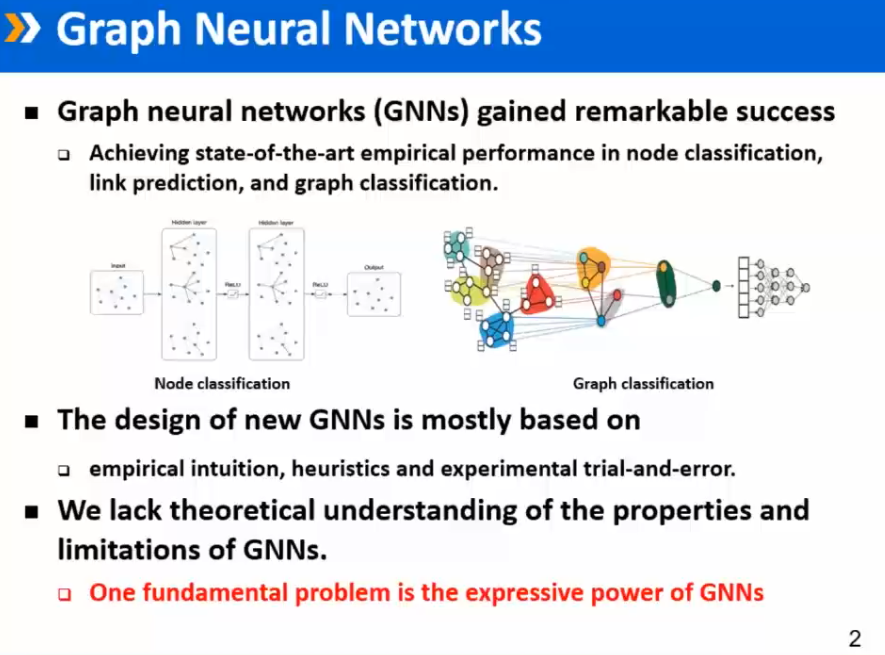
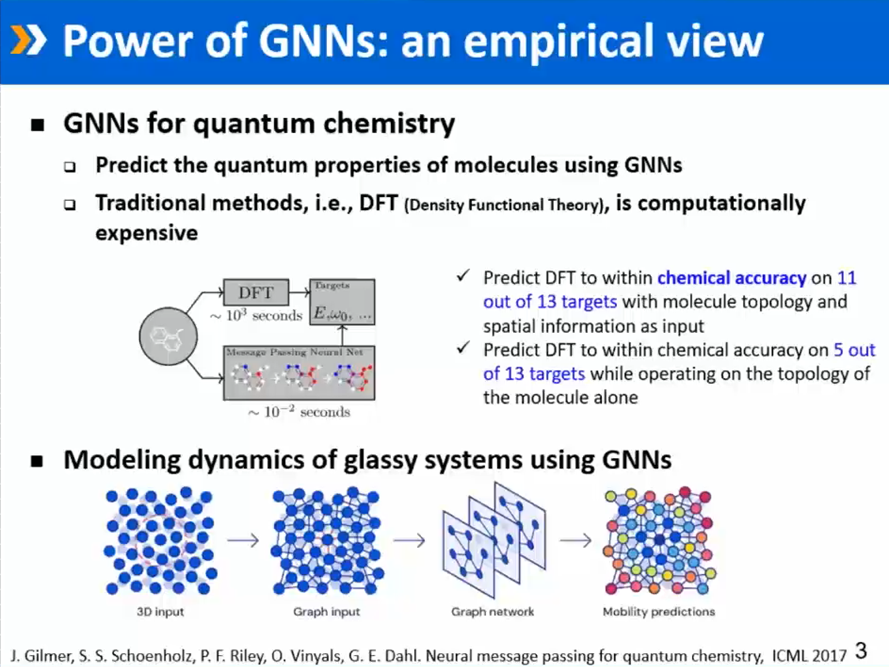
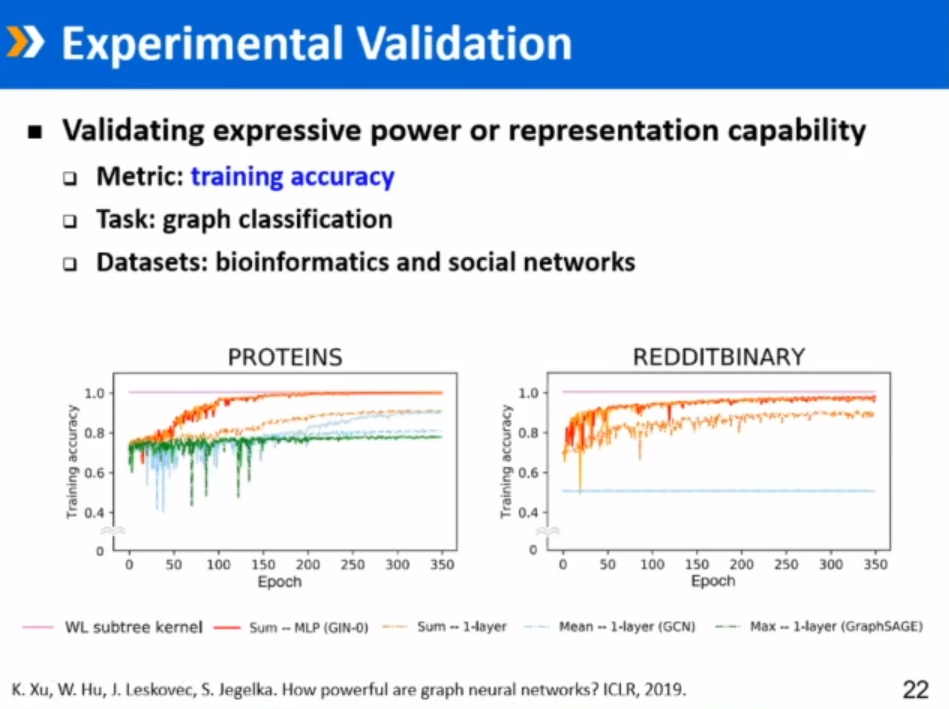
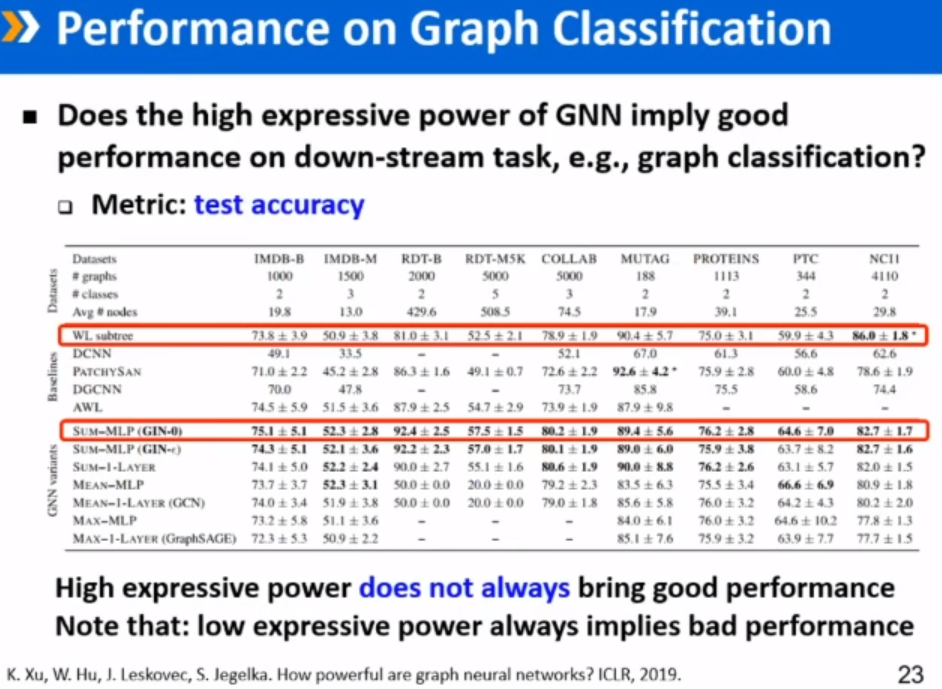
GNN表达能力的经验性证明
GNN基本知识


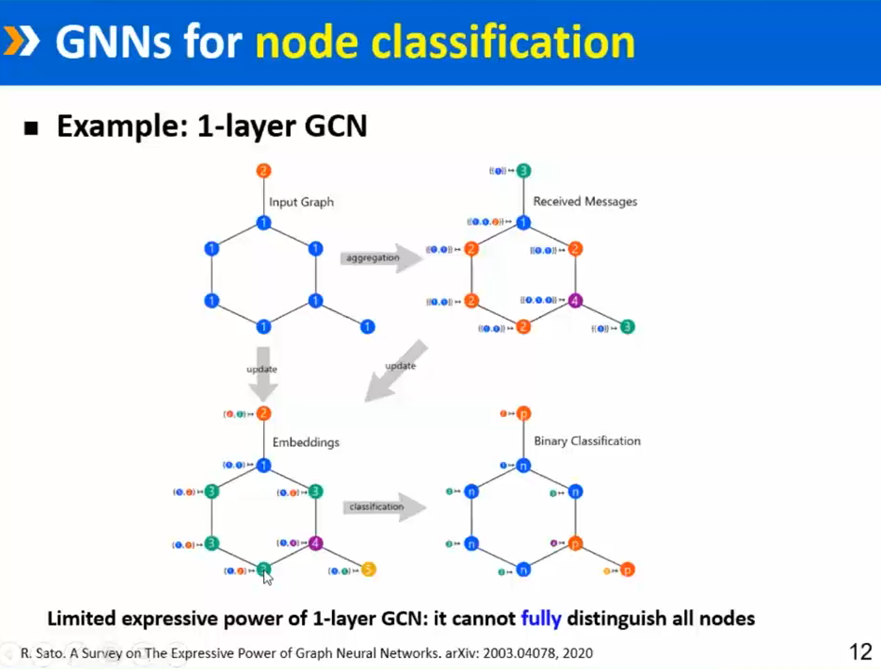
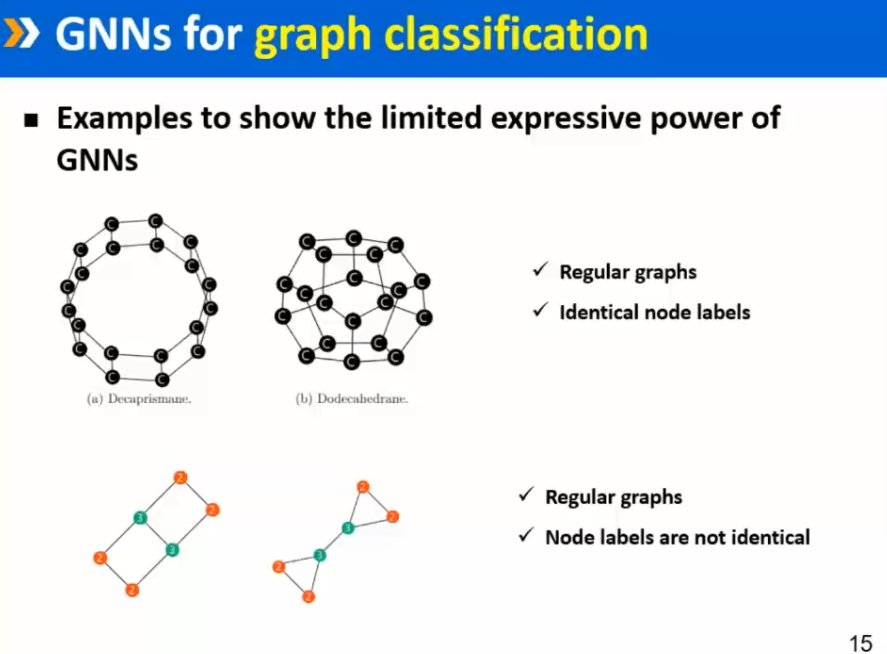
图神经网络的表达能力如何

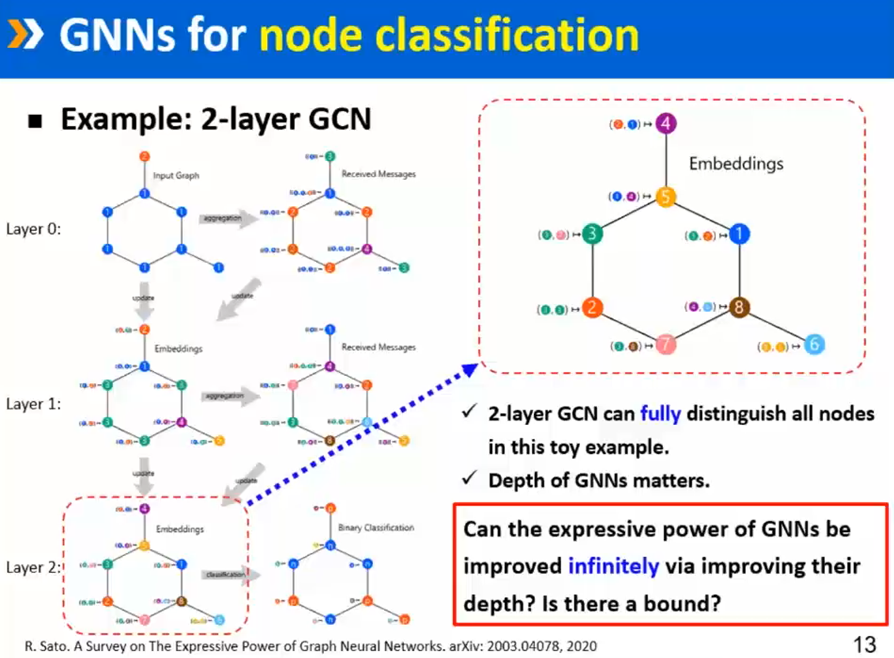


待讨论问题:图神经网络的前沿





登录查看更多
相关内容
沈华伟,博士,中国科学院计算技术研究所研究员,中国中文信息学会社会媒体处理专委会副主任。主要研究方向:社交网络分析、网络数据挖掘。先后获得过CCF优博、中科院优博、首届UCAS-Springer优博、中科院院长特别奖、入选首届中科院青年创新促进会、中科院计算所“学术百星”。2013年在美国东北大学进行学术访问。2015年被评为中国科学院优秀青年促进会会员。获得国家科技进步二等奖、北京市科学技术二等奖、中国电子学会科学技术一等奖、中国中文信息学会钱伟长中文信息处理科学技术一等奖。出版个人专/译著3部,在网络社区发现、信息传播预测、群体行为分析等方面取得了系列研究成果,发表论文100余篇。担任PNAS、IEEE TKDE、ACM TKDD等10余个学术期刊审稿人和KDD、WWW、SIGIR、AAAI、IJCAI、CIKM、WSDM等20余个国际学术会议的程序委员会委员。
Arxiv
20+阅读 · 2020年3月10日
Arxiv
59+阅读 · 2020年1月20日
Arxiv
11+阅读 · 2018年5月16日
Arxiv
8+阅读 · 2018年2月6日
Arxiv
7+阅读 · 2018年1月26日




