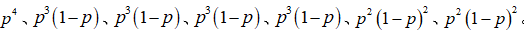数学建模研究过程指导(精编版) Part IV

向上滑动阅览说明及建模目录 

说明：此文稿为朱浩楠老师于2018年11月-12月北京地区联校数学建模活动的课题研究阶段中，每天一篇发布给各课题组的研究方法指导文件的汇总。为方便更多的同学参考使用，现调整为正序后通过遇见数学公众号发布，版权归朱老师和遇见数学公众号所有。

目录

1如何开题

2如何进行问题的分析和数据的获取

3挖掘情境中数学模式的两种方法

4连续模型的使用范围、建立和求解方法

5从连续模型到离散模型&离散模型的常见类型及其研究方法

6确定性与不确定性

7以支持向量机为例谈机器学习的本质

8以神经网络为例谈深度学习的本质

9到底算法能不能算作数学模型或研究成果？

10科学中的香芬迷雾

11问题重述与基本假设部分的检查表

12符号约定部分的检查表

13模型建立部分的检查表

14模型求解部分的检查表

15模型分析部分和参考文献部分的检查表

16数学建模论文摘要的写作建议

17从高中数学体会数学概貌和数学建模

18感性认知如何驱动理性认知

19我们应该抱着什么心态去学习数学与科学

20新生代青年在变革时代中的机会与责任

到底算法能不能算作数学模型或研究成果？

研究方法指导 09

今天的短文很短，但是要谈的是一个非常关键的问题——到底算法能不能算作数学模型或研究成果？这个问题也是很多同学心中的困惑。注意，我下面的论述不仅仅限于数学建模或数学领域，对于一般的科学研究也适用。

我不希望和稀泥，所以一定要斩钉截铁地告诉你一个真相——任何没有经过论证和检验的算法都不能算作科学研究的成果，最多算是科学发现。

有的同学看到这个结论可能会有不同的意见，觉得“很多成果就是一个算法啊”，“历史上很多大的奖项，例如图灵奖中的很多奖，就是颁发给某个算法及其发明者啊”。

你说的没错，而且我非常赞同，在你说的这两个例子里的算法都是科学研究的成果。区别就在于，这些成果并非是简单地提出一个算法，而是配套了严格地论证和检验。而没有严格论证和检验的算法，只能算是科学发现——当然，科学发现不见得就不伟大，我在数学建模课程中一般都会讲到一种方法，叫“重整化方法”，它就是还没有被证明的方法，但是使用起来极为有效，所以在微分方程、神经网络、网格上的概率论乃至超导理论中都有非常关键的计算上的使用。但是它还没有被证明，所以即使很有效，也只能叫做科学发现，而非科学成果。

很多数学建模的初学者或者做项目研究的初学者很容易走入到一个误区，他们提交上来的论文或者研究报告中，充斥着流程图和算法代码（或伪码）。但是通篇看下来，并没有论证过算法的有效性，也没有建立出算法基于的数学模型。所以在应用时，即使是面对类似的问题，别人也不敢使用，或者需要重新建立数学模型去使用。这其实已经偏离了科学研究的主要目的之一——“建立泛知识体系以方便迁移使用”。

但是话说回来，如果你研究的是一个操作性很强的问题，例如研究魔方或者拼图或者某些游戏的必胜策略，那么你肯定是要给出一个算法（注意：给出算法不是只给代码，算法需要用语言文字精准表达，代码一般都放在附录中，因为同一个算法可以用不同的编程语言实现，但是代码不可以）。但是算法后面一定要有论证和分析，以及实证效果的检验与说明。实际上，科学研究中通常称一个算法是“合格”的，就指的是这个算法既经过了理论的论证，又经过了实证检验。

如果一个算法很难进行有效性的理论证明，例如刚才说过的“重整化方法”，那么很有可能你遇到了一个值得用更大力气更加深入研究下去的领域。这是非常幸运的，因为你开创了一个新的领域。但是前提是你要能抓的住这份幸运，而抓住这份幸运需要三个前提：（1）扎实的学术基本功；（2）对未知的好奇心驱动；（3）对自然真理和实践敬畏以寻求理论论证同时配以实证检验。

科学中的香芬迷雾：重整化方法

研究方法指导 10

为了形象展现重整化思想，下面我通过图像处理和超导物理中的渗流理论来分别阐述。

1.重整化思想用于图像处理

熟悉卷积神经网络的同学都知道，最大池化为卷积神经网络中的关键技巧。最大池化可以看作重整化思想的一个应用。图1是我爱人2018年6月的一张生活照，原始尺寸为1440像素×1080像素，我们将其视为一个以向量为元素的张量 G=(gij)，其中 gij 代表照片中第 i 行第 j 列的RGB向量（一个三维向量，三个坐标分别代表三原色的色阶），i=1,2,...,1440，j=1,2,...,1080。取定 L∈N，L<1080，称 GL=(giL,jL) 为 G 的重整化张量，其中 i=1,2,...,⌊1440/L⌋ ，j=1,2,...,⌊1080/L⌋ 。称为重整化比例。表1中给出了图1在不同重整化比例下的重整化图像。

图1 我爱人在2018年6月于京郊古北水镇拍摄的一张生活照，像素尺寸为1440像素×1080像素。

从图1和表1中诸图的对比中可以看到，随着重整化比例逐渐升高，重整化后的图片尺寸越来越小（实际上，像素数量大约变为原来的1/L²），但图片中的信息也越来越少，图片越来越粗糙。到 L=30 和 L=50 时依然可以看到人像轮廓，但是到 L=100 时就很难分辨出人像了。

 

2. 1.重整化思想用于渗流理论

重整化方法可以看作是对信息的采样。采样越密集，则信息流失越少，但样本规模越大；采样越稀疏，则信息流失越多，但样本规模越小。

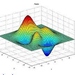
神奇的是，重整化方法蕴藏着深刻的自然法则。在超导和流体力学的研究中，有一种理论称为渗流理论。渗流理论在数学上隶属于随机图论，是对自然规律进行数学建模的一个典型例子。假设平面内有一个尺寸非常大（或无穷大）的方格网络（如图2所示），其中每个网格各自独立地以概率 p，p∈(0,1) 染成黑色，以概率 1-p 染成白色。如果两个黑色网格有一条边重合，则称这两个网格连通；否则称这两个网格不连通（如图3所示）。渗流理论的问题是：当所有网格均染色后，从网络最上方到最下方是否存在一条由黑色网格形成的通路？如果存在这样的通路，概率 p 的最小值为多少？这个最小的概率值 p 如果存在，则被称为临界概率。

图2 平面上横、纵尺寸均为无穷大的方格网络。

                                                    

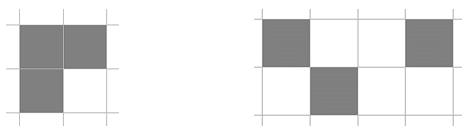
图3 连通（左）和不相通（右）的黑色网格。

渗流理论目前已发展为一套专门的分支，本书不做展开讨论。下面要说的是利用重整化方法来求临界概率的近似数值。

一个基本的思路是：如果能将田字形排布的4个相邻染色方格按照“是否连通上端与下端”的准则对应为一个新网络中的一个染色方格，并重复这个步骤，那么网络上方和下方的方格的距离就被逐渐降低，直到化为一个染色方格，则连通性的判别就迎刃而解了。为了让这个过程得以进行下去，对应关系格外重要。依据图3中对于连通与否的定义，可得如下对应：

图4 重整化对应法则，依据上、下两端是否连通。

假设临界概率存在，重整化过程提供了一种计算其大约数值的方法：

由于各个方框的染色情况是相互独立的，图4中箭头左侧7种染色出现的概率分别为

同时箭头右端染色出现的概率为 p，根据重整化思想和概率的分类加法原理，可得方程

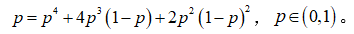
解得 p=(√5-1)/2≈0.618。这个数值刚好为黄金分割比例。作为例子，图5中给出了 p=0.3, p=0.5, p=0.618 和 p=0.8 时对一个 30×30 方形网络的随机染色图。

 p=0.3, p=0.5, p=0.618, p=0.8
图5 不同染色概率 p 下对 30×30 方形网络的随机染色结果。

如果我们换一种重整化模式，将九宫格排列的的9个方格按照类似于图4中的对应法则对应到一个方格，并重新计算临界矩阵的值，可得（具体计算留给同学们作为练习，并非很容易，可以作为排列组合的一个很好的训练）

p≈0.614。

所以重整化模式的改变会影响求得的值。实际上，重整化模式中，当 n 的取值改变时，将 n×n 的 n² 个方格按照类似于图4中的方法对应到一个方格，计算 p 出的值（记为 pn）均不相同。我们不加证明地指出，存在 ，且 。

 

3.重整化思想并非是单一方法

重整化思想的奇妙之处在于，它与不同的学科、领域、分支结合之后，都能生发出具有该学科、领域、分支的独立方法。重整化思想模拟了人类对自然的理解方式——人类的记忆只储存概貌，而非细节，就像我们对父母的长相很熟悉，但是如果没有受过专业训练，很难说出父母的每一个体貌细节，而往往只能描述其体貌特征。人是靠特征去理解自然界的，重整化是对特征的一种提取方式。因为不同的学科、领域、分支的特征的体现形式不同——图像、声音、颜色等等，所以重整化思想在其中的应用形式会有差别。

一个非常可惜的事情是，重整化方法在很多时候经过实证检验很有效果，但是很难对其有效性做理论证明。例如刚才我们说的  这件事，其实就很难证明。