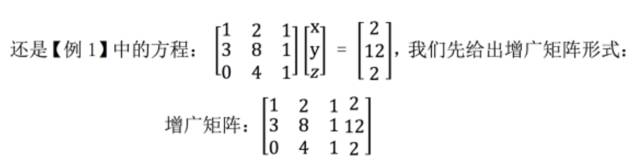干货|MIT线性代数课程精细笔记2

干货|MIT线性代数课程精细笔记[第二课]

前言

MIT线性代数课程精细笔记[第一课]笔记见MIT线性代数课程精细笔记1。

该笔记是连载笔记，希望对大家有帮助。

1

知识概要

这一节中我们介绍一下消元法，即是上一节中我们提到的“系统化”求解方程所用的方法，通过矩阵消元运算可以很轻松地求解复杂方程。

另外还介绍了消元矩阵，即我们的消元运算在矩阵乘法中所表现的形式。并从消元矩阵引入，介绍逆矩阵的基础知识。

2

 消元法求解方程 

2.1 消元法介绍

对于一些“好”的系数矩阵（可逆矩阵）A 来说，我们可以使用消元法来求解方程 Ax = b，我们还是从一个例子谈起。

所谓矩阵的消元法，与我们初等数学中学习的解二元一次方程组的消元法其实师出同门，都是通过将不同行的方程进行消元运算来简化方程，最后能得到简化的方程组，只不过这里我们把系数单独抽出来进行运算，寻找一种矩阵情况下的普遍规律而已。

注：

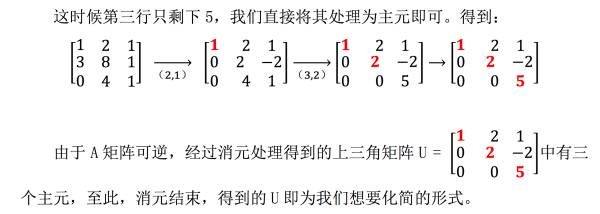
并不是所有的 A 矩阵都可消元处理，需要注意在我们消元过程中，如果主元位置（左上角）为 0，那么意味着这个主元不可取，需要进行 “换行”处理：

首先看它的下一行对应位置是不是 0，如果不是，就将这两行位置互换，将非零数视为主元。如果是，就再看下下行，以此类推。若其下面每一行都看到了，仍然没有非零数的话，那就意味着这个矩阵不可逆，消元法求出的解不唯一。

下面是三个例子：

2.2 回带求解

其实回带求解应该和消元法同时进行，只不过本课中以及一些软件工作原理中它们是先后进行的，所以我们这里分开讨论，先介绍增广矩阵：

一下子就看出来了，就是把系数矩阵 A 和向量 b 拼接成一个矩阵就行了。

3

 消元矩阵 

3.1 行向量与矩阵的乘法

上面的消元法是从简单的变换角度介绍了消元的具体操作，接下来我们需要 用矩阵来表示变换的步骤，这也十分有必要，因为这是一种“系统地”变换矩阵的方法。

导致错误。其实学过矩阵之间的乘法之后这些东西都极为简单，但这里还是建议大家尽量从向量的角度去考虑问题。

3.2 消元矩阵介绍 

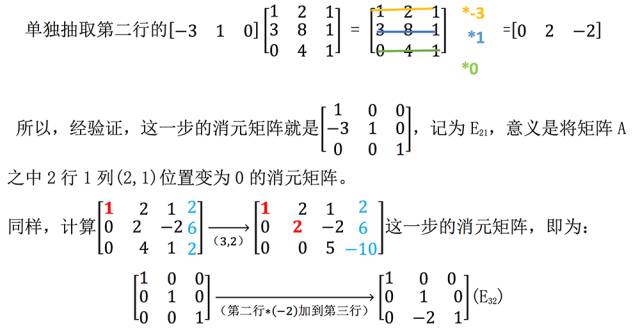
好的，接下来是重点。学会了行向量与矩阵之间的乘法，我们就可以使用行 向量对矩阵的行做操作了。所谓消元矩阵，就是将消元过程中的行变换转化为矩阵之间的乘法形式。

我们消元过程是将第一行乘 -3 加到第二行，这是对第二行的操作，那么就从单位阵的第二行着手：

3.3 行交换矩阵与逆矩阵

3.3.1 行变换与列变换

3.3.2 逆矩阵初探

可以说我们学会了消元矩阵，就相当于我们可以用矩阵乘法对一个矩阵进行任 何变化了，那么我们考虑一个反过程，即我们把一个消元结束的矩阵 U 如何变为 未经消元的矩阵 A 呢？

答案就是乘上一个逆矩阵。

4

 学习感悟

---

本节从矩阵消元的角度，介绍解方程的通用做法，并介绍了消元矩阵，使我们从矩阵乘法层面理解了消元的过程，并延伸了消元矩阵的应用：就是基于单位阵 I 的变化，对矩阵 A 进行行列变换的过程。

这一节的消元法以后会常用，要熟练掌握才可以。

希望对大家有帮助~

---

☞  哈尔莫斯：怎样做数学研究

☞  扎克伯格2017年哈佛大学毕业演讲

☞  线性代数在组合数学中的应用

☞  你见过真的菲利普曲线吗？

☞  支持向量机(SVM)的故事是这样子的

☞  深度神经网络中的数学，对你来说会不会太难？

☞  编程需要知道多少数学知识？

☞  陈省身——什么是几何学

☞  模式识别研究的回顾与展望

☞  曲面论

☞  曲面论（第二讲）

☞  曲面论（第三讲）

☞  自然底数e的意义是什么？

☞  如何向5岁小孩解释什么是支持向量机（SVM）？

☞  华裔天才数学家陶哲轩自述

☞  代数，分析，几何与拓扑，现代数学的三大方法论

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域。

稿件一经采用，我们将奉上稿酬。

投稿邮箱：math_alg@163.com