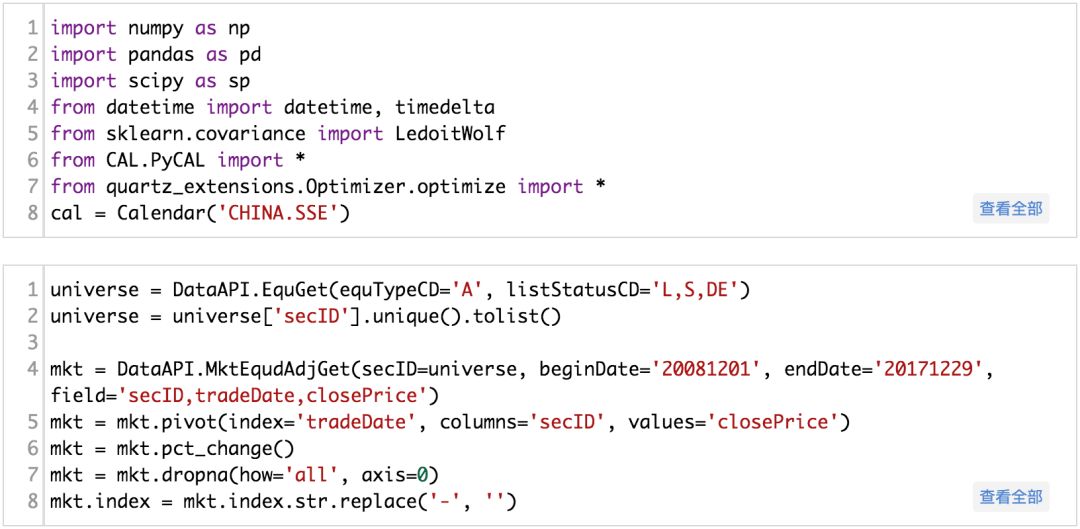
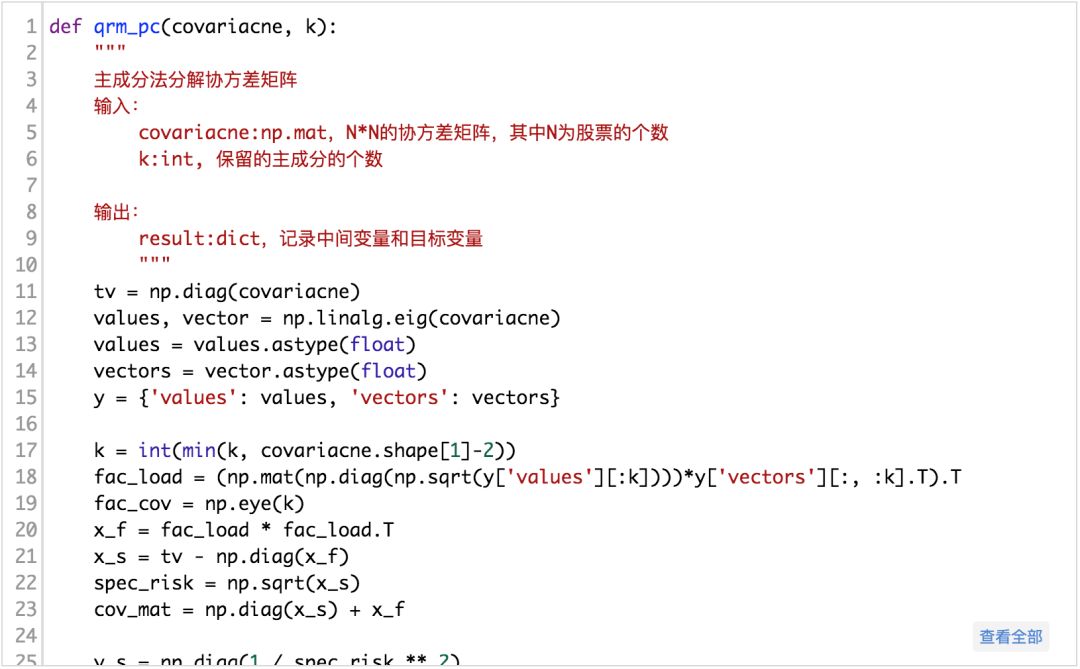
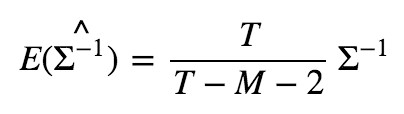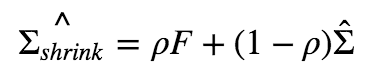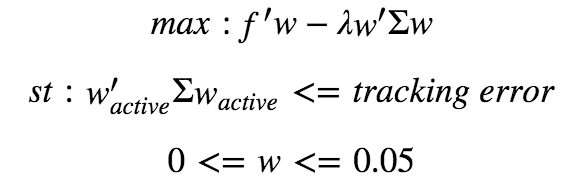【量化学堂】统计风险模型再探——与基本面风险模型的比较

2018 年 5 月 17 日 优矿量化实验室 充满智慧的👉

在前面的文章《统计风险模型初探》里，我简单的对统计风险模型进行了大致的探索，实测下来效果一般。本文参考东方证券《风险模型提速组合优化的另一种方案》，将统计风险模型与压缩估计法进行结合，同时将得到的协方差矩阵的预测与优矿的基本面风险模型所得到的协方差矩阵的预测进行对比测试。本文有两个目的:

探索因子模型在求解组合优化问题上是否具有计算优势
比较统计风险模型与基本面风险模型孰优孰劣

（完整版请点击文末“阅读原文”获取）

1模型原理

关于统计风险模型的原理在前面的文章已经做初步的说明。此处不再赘述，这次把对协方差矩阵进行分解的代码一并提供，也算是一个小小的福利吧。其实对于压缩估计，经常使用优矿的矿友一定不会陌生，此前占据社区头条一年多的热帖MultiFactors Alpha Model - 基于因子IC的多因子合成里面就介绍了这种方法。不过该文是对IC的协方差矩阵进行压缩，意义不大(在因子数量不多的情况下，我们能够直接把这个协方差矩阵算出来并保证其性质良好)。本文将这种方法应用于股票收益率的协方差矩阵上。（文章可在优矿社区获取）

从统计的角度来说，样本协方差的估计完全依赖于数据，而先验的协方差矩阵可以来源于主观的判断、历史经验或者模型。样本协方差矩阵是无偏的，但是有大量的估计误差。而先验的协方差矩阵由于具有严格的假设，因此其设定存在偏差，但是其待估的参数少，所以估计误差也小。事实上，当股票数量很多时，样本协方差矩阵不一定可逆，即使它可逆，协方差矩阵的逆矩阵也不是协方差矩阵逆矩阵的无偏估计，实际上在正态分布假设下有：

这时候，如果T表示观察的期数，M表示股票数量，这时候，如果T和M很接近，那就会给模型带来很大的偏误。

协方差的压缩估计量可以表示为样本协方差矩阵和压缩目标的一个线性组合，即：

其中F为压缩目标，Σ̂ 为样本协方差矩阵，ρ为压缩强度。

压缩估计量的关键在于压缩强度的确定，可以通过一定的损失函数来估计压缩强度。Ledoit&Wolf(2013)使用协方差矩阵压缩估计量与真实协方差矩阵之间的距离来作为损失函数，压缩强度则可以最小化损失函数求解得出。而压缩目标的选择有以下形式进行参考：

Ledoit(2004) 单参数形式，可以表示为方差乘以一个单位矩阵
Ledoit(2003b) CAPM单因子结构化模型估计
Ledoit(2003a) 平均相关系数形式

本文使用了第一种形式。

2主成份个数的选择

事实上，统计风险模型好比是使用了统计学上的因子分析法，甚至更具体的是因子分析当中的主成份法。在前文当中，我们也留下来这样一个思考，保留的公共因子的个数k取多少合适？这里，我们使用主成份分析中的方差解释度这个概念，计算前k个最大的特征值之和占所有特征值之和的比例。

（完整版请点击文末“阅读原文”获取）

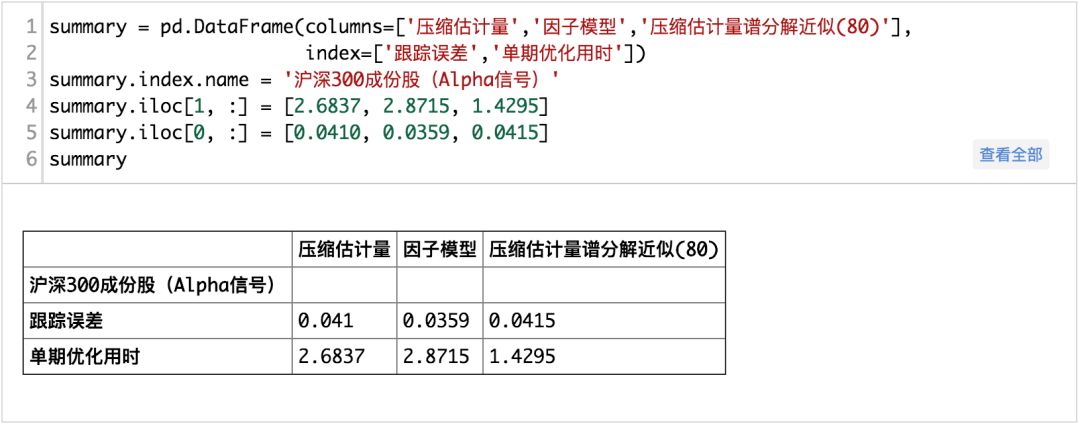
从上表的结果来看,对于沪深300成份股、中证500成份股前20个最大特征值之和占比就超过了50%；当k取100时,沪深300成分股超过了80%，但是中证500成份股依然没有达到80%，并且对于全市场来说，k取100方差解释度不足70%。

Zura Kakushadze & Willie Yu在《Statistical Risk Models》论文当中也提到了两种关于k的选择的方法，论文附录了R语言的代码，有兴趣的读者可以参考一下。

3实证分析

cvxpy在其文档中提供了一个组合优化的例子，在其例子中，详细的说明了对于一个标准的组合优化问题，使用因子模型进行组合优化的时间复杂度和使用原始的股票之间的协方差矩阵的时间复杂度的大小。不难发现，使用因子模型进行组合优化在计算上有优势。

简单起见，我们使用四个例子：沪深300指数增强（成份股内，信号随机生成），沪深300增强（全市场，信号随机生成），沪深300指数增强（成份股内，Alpha信号），沪深300增强（全市场，Alpha信号）。读者也可以参考本文构造例子进行测试。本文分别测试标准压缩估计量，风险模型，和不同K取值下谱分解近似方法的优化速度和效果。组合优化问题设置如下:

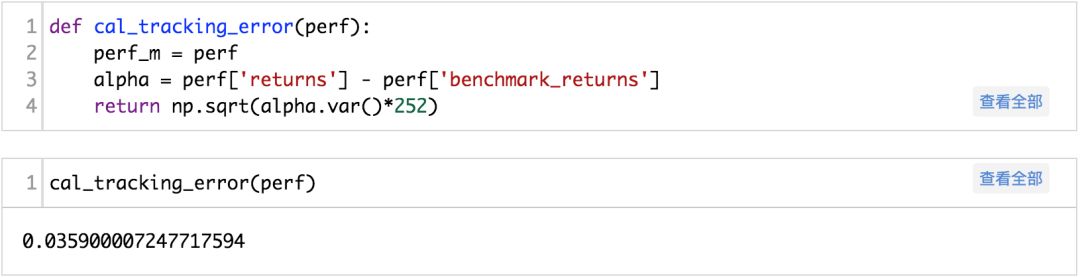
为了避免其它约束对风险预测的影响，我们只设置跟踪误差约束，以及个股权重的上限,λ设为0.05。我们比较组合实际的跟踪误差与预先设置的跟踪误差的差别。同时为了检验我们模型对风险的预测能力，我们使用随机的组合来进行测试。再把这些结果，输入到优化器内进行求解，得到权重之后，使用优矿最新的quartz回测框架进行测试(新版回测速度很快，大家多多使用，多提建议啊)，回测的模板将在附录当中给出。下表给出了统计结果(求解时间包括数据载入的时间，实际上，在问题维度较大的情况下，我们本地测试下来，我们的优化器的性能要显著优于cvxpy+ecos)

我们做两组实验,一组随机生成Alpha信号,一组使用真正的信号.通过两种不同的场景综合地进行比较：

（完整版请点击文末“阅读原文”获取）

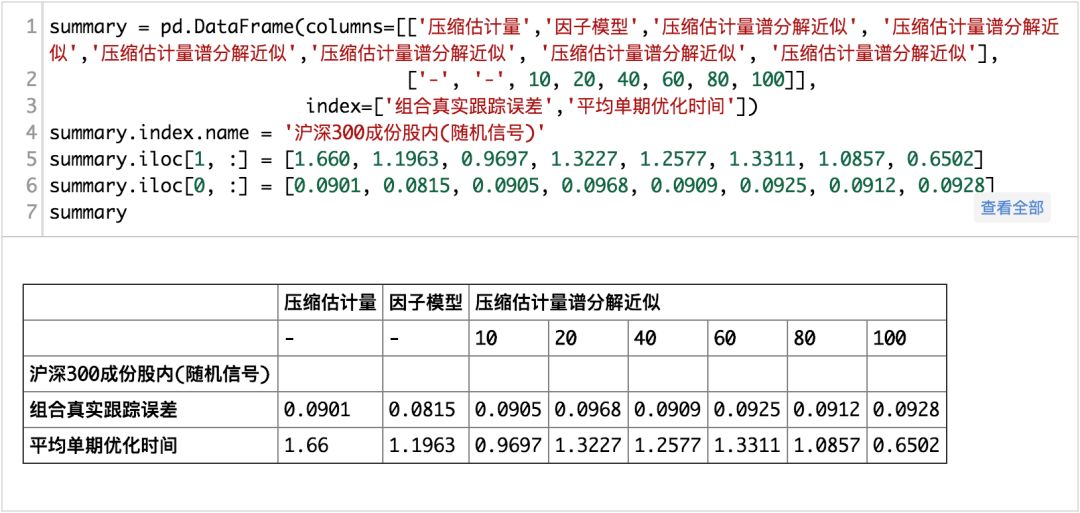
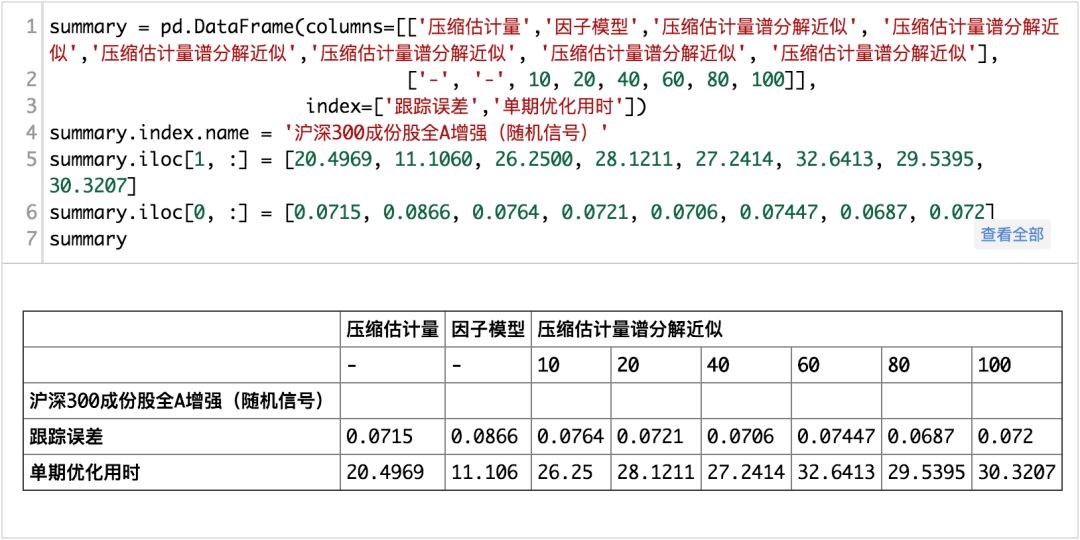
从结果来看：

单期优化用时与k的取值并没有呈现出明显的单调性，而且所花费的时间甚至比简单的压缩估计要多。
同时我们可以看到无论是使用压缩估计量，还是使用压缩估计量谱分解近似所得到协方差矩阵来控制组合跟踪误差，效果均要略优于基本面风险模型。
也就是说，如果单单是从组合风险的估计上，压缩估计+谱分解理论上是可行的。

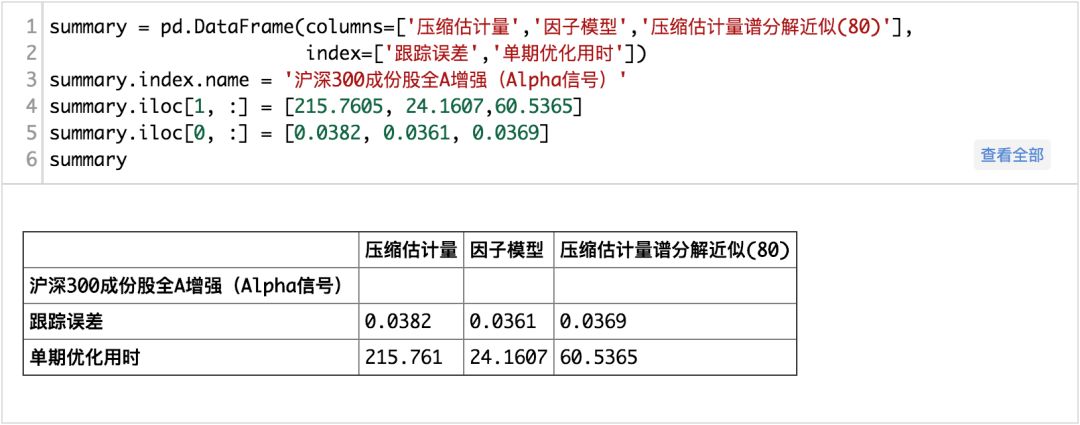
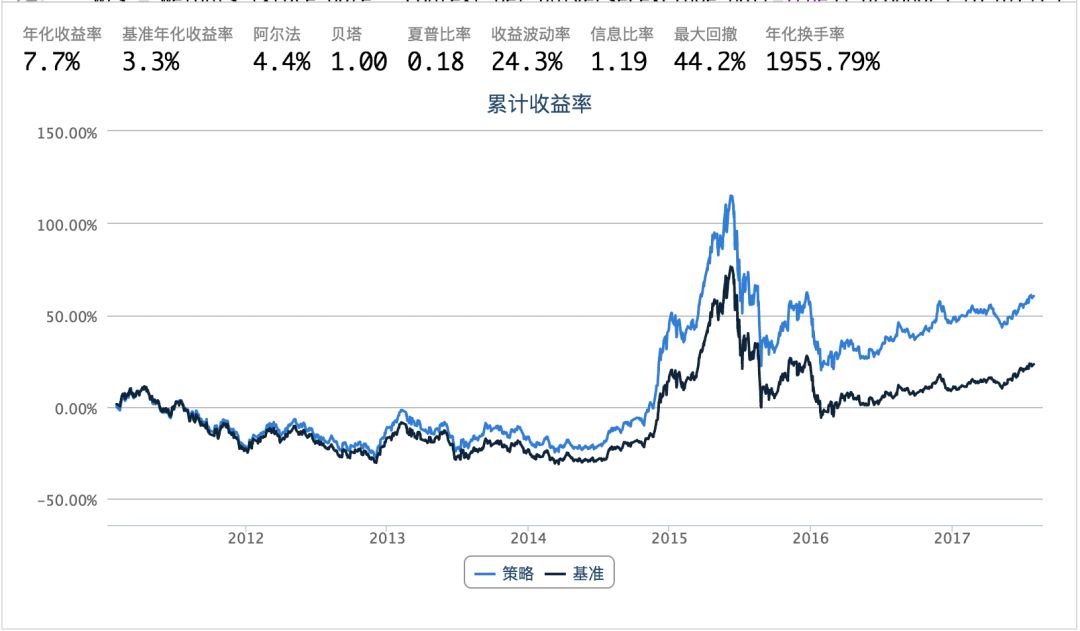
那么实际上是否真的可行？本文使用两一组真实的信号来进行分析，一组为全A范围内的沪深300指数增强策略，另一组为沪深300成分股内的指数增强测了。在使用Alpha信号进行对比测试的时候,我们去除组合优化当中个股权重的上限约束,将跟踪误差约束目标值进一步下调至年化3%,然后比较压缩估计量,因子模型,以及谱分解近似(80个主成分)三个模型的效果。

（完整版请点击文末“阅读原文”获取）

从真实的信号测试的结果来看，在全A范围内使用压缩估计所耗费得到的协方差矩阵进行组合优化所求解的时间明显要多于基本面风险模型和，而压缩矩估计+主成份分解的方法次之，基本面风险模型是最快的而且也是效果最好的，而在沪深300成分股内，则不明显。整体上来说，使用压缩矩估计+主成分分解来估计协方差矩阵是可行的。

回测部分可以使用下面的框架，对于不同的股票池，只需要修改对应不同的域,不同的权重输入即可。

（完整版请点击文末“阅读原文”获取）

4结论

风险模型主要实现三个功能：组合优化、绩效归因、以及Alpha因子中性化。后面两个功能都需要基本面风险模型的相关数据，估算协方差矩阵可以使用结构化因子模型，也能通过纯统计方法（例如:压缩估计量，统计风险模型）得到。
用因子模型的好处是可以大幅缩减要估计的参数数量,降低估计误差，同时也降低了组合优化过程中协方差相关计算的计算复杂度，在股票数量较多时可以将组合优化速度提升一至两个数量级，节约策略回溯调试时间。
本文我们先用线性压缩估计量方法得到协方差矩阵估计，再对协方差矩阵进行因子分析，得到类似于基本面风险模型的结构，然后对比这三类模型使用的效果。
但是从本文测试的结果来看，基本面风险模型对风险的估计略优于统计风险模型，使用真实的信号求解组合优化问题速度也会快一些，但最终差别不大。