初学者系列:递归神经网络简介-实现文本情感分类
导读
递归神经网络(RNN)是一种专门处理序列的神经网络。它们经常用于自然语言处理(NLP)任务,因为它们在处理文本方面相当有效。在这篇文章中,我们将探讨RNN是什么,了解它们是如何工作的,并在Python中从头开始构建一个真正的RNN(仅使用numpy)。
作者 | Victor Zhou
编译 | Sha Li
为什么选择RNN
01
最初的神经网络(以及CNN)的一个问题是它们只能使用预定大小:它们采用固定大小的输入并产生固定大小的输出。而 RNN可以让我们将可变长度序列作为输入和输出。 以下是RNN的外观示例:
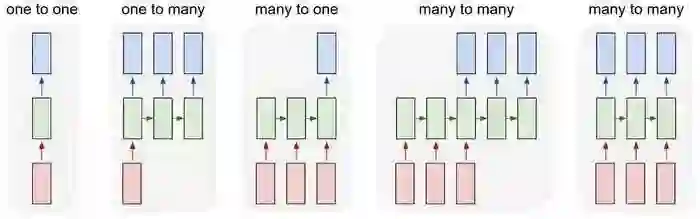
输入为红色,RNN本身为绿色,输出为蓝色。
图片来源于:Andrej Karpathy
这种处理序列的能力使RNN非常有用。 例如:
机器翻译(例如Google翻译)由“多对多”RNN完成。 原始文本序列送入RNN,RNN产生翻译的文本作为输出。
情感分析(例如,这是一个积极的还是负面的评论?)通常是用“多对一”的RNN完成的。 将要分析的文本输入RNN,然后生成单个输出分类(例如,这是一个积极的评论)。
在本文后面,我们将从头开始构建“多对一”RNN,以执行基本的情感分析。
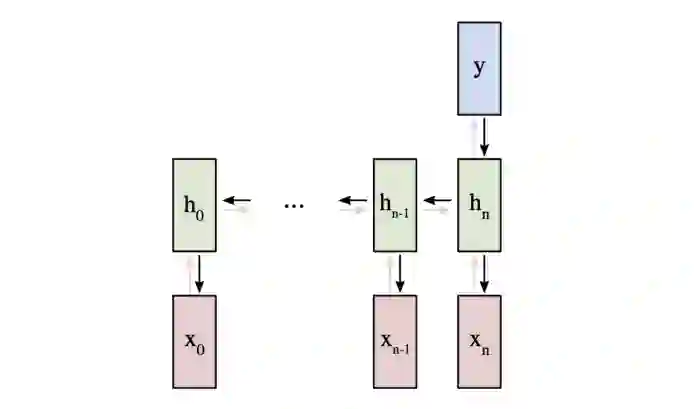
RNN是怎样工作的
02
让我们考虑一个“多对多”的RNN,其输入x_0,x_1,... x_n想要产生输出y_0,y_1,... y_n。 这些x_i和y_i是矢量并且可以具有任意尺寸。
RNN通过迭代地更新隐藏状态h来工作,隐藏状态h是可以具有任意维度的向量。
在任何给定的步骤t:
使用先前的隐藏状态h_{t-1}和下一个输入x_t来计算下一个隐藏状态h_t。
使用h_t计算下一个输出y_t。
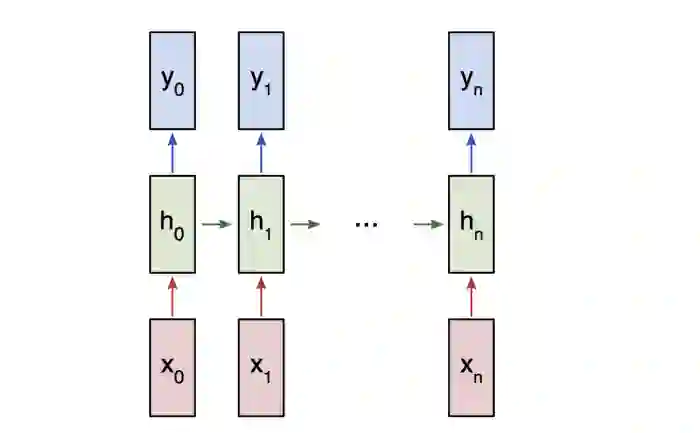
“多对多” RNN
这就是RNN工作的原因:RNN的每一步都使用相同的权重。 更具体地说,典型的 RNN仅使用3组权重来执行其计算:
W_{xh}用于所有x_t→h_t 的连接
W_{hh},用于所有h_{t-1}→h_t的连接
W_{hy},用于所有h_t→y_t的连接
我们还将为我们的RNN使用两个偏差:
b_h,在计算h_t时添加
b_y,在计算y_t时添加
我们将权重表示为矩阵,将偏差表示为向量。 这3个权重和2个偏差构成了整个RNN!
以下是将所有内容组合在一起的公式:
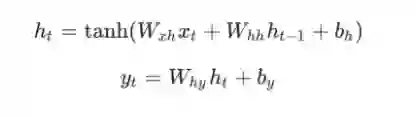
tips:不要浏览这些方程式。 停下来盯着这一分钟。 另外,请记住权重是矩阵,其他变量是向量。
对所有权重使用矩阵乘法,并将偏差添加到所得结果中。 然后我们使用tanh作为第一个等式的激活函数(但也可以使用其他激活,如sigmoid)。
开始实践
03
我们将从头开始搭建RNN以执行简单的情感分析任务:确定给定的文本字符串是正还是负。
以下是我为这篇文章整理的小数据集中的一些示例:

由于这是一个分类问题,我们将使用“多对一”RNN。 这类似于我们之前讨论过的“多对多”RNN,但它只使用最终隐藏状态来生成一个输出y:
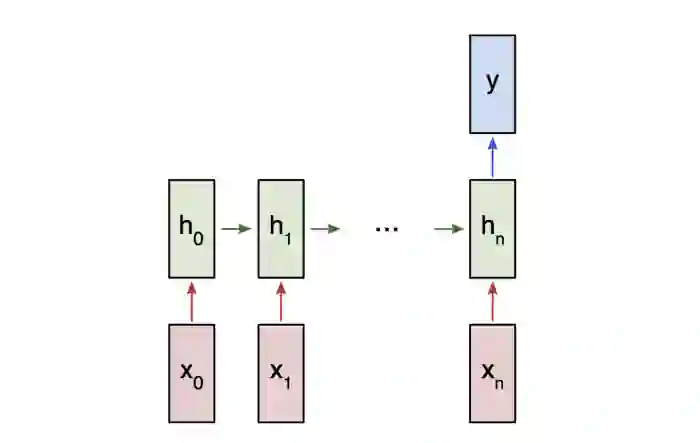
“多对一”RNN
每个 将是表示文本中的单词的向量。 输出y将是包含两个数字的向量,一个表示正数,另一个表示负数。 我们将应用Softmax将这些值转换为概率,并最终在正/负之间做出决策。
让我们开始构建我们的RNN!
预处理
04
我之前提到的数据集包含两个Python字典:

我们必须进行一些预处理才能将数据转换为可用的格式。 首先,我们将构建我们数据中所有单词的词汇表:
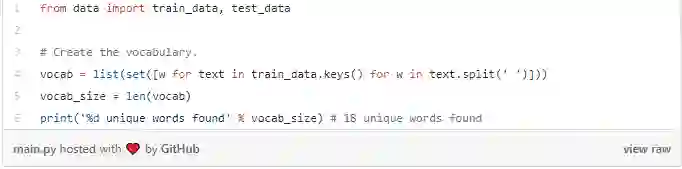
vocab现在包含至少一个训练文本中出现的所有单词的列表。 接下来,我们将指定一个整数索引来表示我们词汇表中的每个单词。
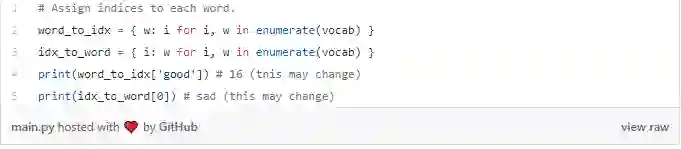
我们现在可以用相应的整数索引表示任何给定的单词! 这是必要的,因为RNN无法理解单词 ,我们必须给它们数字。
最后,回想一下我们RNN的每个输入 都是一个向量。故我们将使用one-hot矢量,其中包含除了单个零之外的所有零。 每个one-hot矢量中的“1”将位于单词的相应整数索引处。
由于我们的词汇表中有18个独特的单词,因此每个 将是一个18维的one-hot矢量。
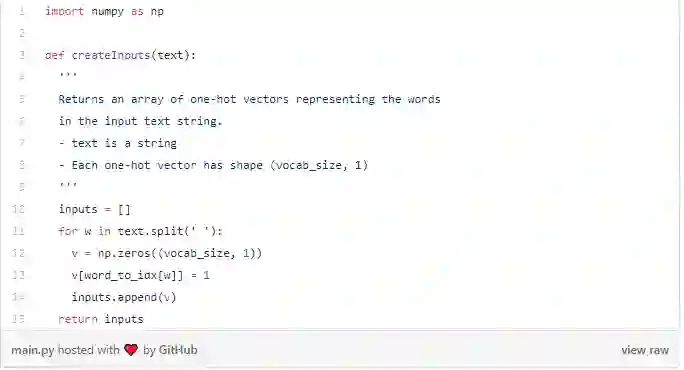
稍后我们将使用 createInputs( )创建矢量输入以传入我们的RNN。
前向传播阶段
05
现在是时候开始构建我们的RNN了! 我们首先初始化RNN需要的3个权重和2个偏差:
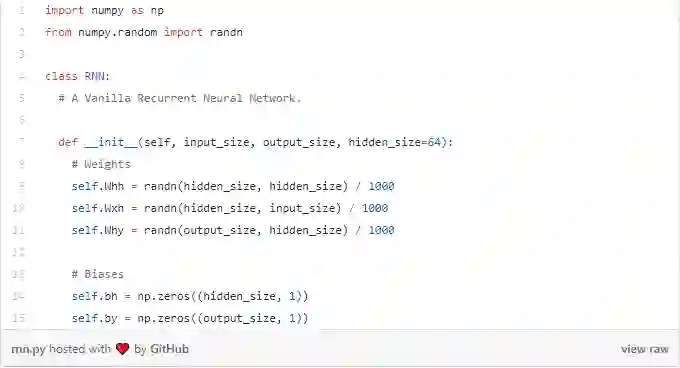
tips:我们除以1000以减少权重的初始方差。 这不是初始化权重的最佳方法,但它很简单,适用于这篇文章。
我们使用np.random.randn()从标准正态分布初始化权重。
接下来,让我们实现我们的RNN前向传播。 还记得我们之前看到的这两个方程吗?
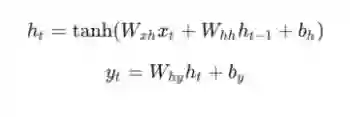
以下是该方程式在代码中的表示:
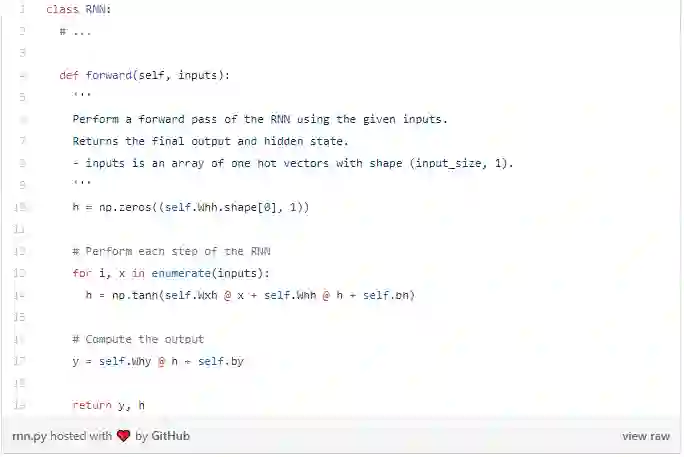
很简单吧! 请注意,我们在第一步中将h初始化为零向量,因为在此之前没有隐藏状态h。我们来试试吧:
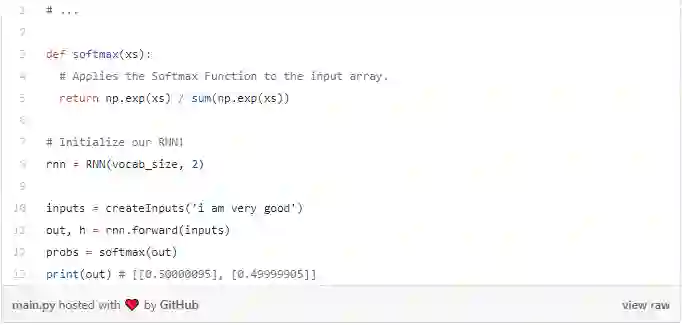
我们的RNN有效,但它还不是很有用。 让我们改变一下......
反向传播阶段
06
为了训练我们的RNN,我们首先需要一个损失函数。 我们将使用交叉熵损失,这通常与Softmax配对。 这里我们按如下公式计算它:
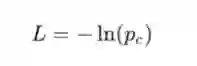
p_c为我们的RNN预测正确等级(正面或负面)的概率。 例如,如果我们的RNN预测正面文本为90%,那么损失是:
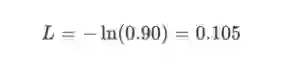
现在我们有了损失,我们将使用梯度下降训练我们的RNN,以尽量减少损失。 这意味着我们要开始计算梯度了!
Note:以下部分假定了你已经了解多变量微积分的基本知识。 如果你愿意,你可以跳过它,但即使你不太了解,我也建议去浏览。 在我们推导出结果时,我们将逐步编写代码,甚至表面层次的理解也会有对你有所帮助。
准备好了么?我们继续进行。
定义
首先,一些定义:
设y代表我们RNN的原始输出。
设p表示最终概率:p = softmax(y)。
设c指某个文本样本的真实标签,换句话说就是“正确”类。
令L为交叉熵损失:L=-ln(p_c)
设W_{xh},W_{hh}和W_{hy}是RNN中的3个权重矩阵。
设b_h和b_y为RNN中的2个偏置向量。
设置
接下来,我们需要编辑前向传播阶段以缓存一些数据,便于在反向传播中使用。 在我们处理它的同时,我们还将为我们的反向阶段设置框架。 这是看起来像:

梯度
这是数学时间! 我们首先计算∂L/∂y。 我们知道:

我将使用链规则作为练习留下实际的∂L/∂y推导,但结果非常好:
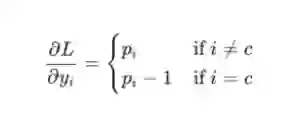
例如,如果我们有p = [0.2,0.2,0.6]并且正确的类是c = 0,那么我们得到∂L/∂y= [ - 0.8,0.2,0.6]。 这也很容易变成代码:
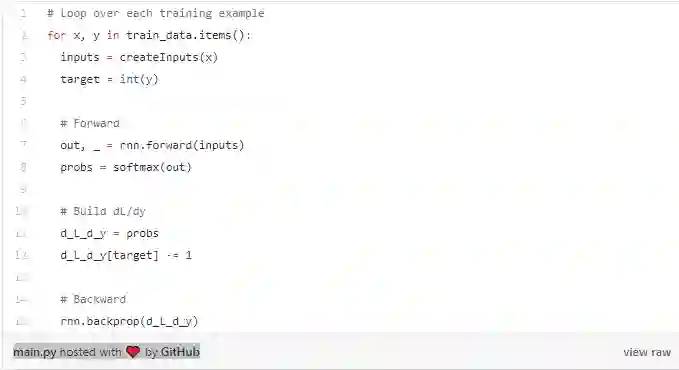
接下来,让我们来对梯度进行分析看看是什么原因并且通过什么方式可以仅将最终隐藏状态转换为RNN的输出。 我们有:
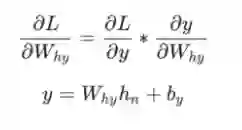
其中h_n是最终的隐藏状态。 从而,

同样地,
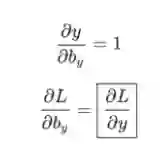
我们现在可以开始实现backprop()了!
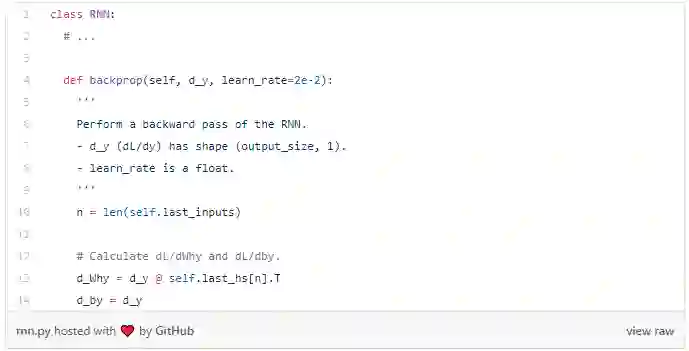
Note:我们之前在forward()中创建了self.last_hs。
最后,我们需要W_{xh},W_{hh}和b_h的梯度,这些梯度在RNN反向传播期间的每一步都使用。 我们有:
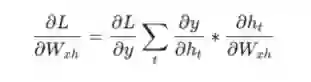
因为改变W_{xh}会影响每个h_t,它们都会影响y并最终影响L.为了完全计算W_{xh}的梯度,我们需要反向传播所有时间步长,这称为随时间反向传播(BPTT):
W_{xh}用于所有 x_t→h_t前向链接,因此我们必须反向传播回每个连接。
一旦我们到达给定的步骤t,我们需要计算∂h_t/∂W_{xh}:
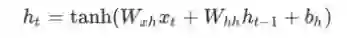
tanh的导数是众所周知的:
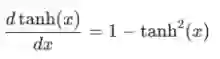
我们像往常一样使用链式规则:
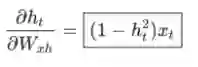
同样地,
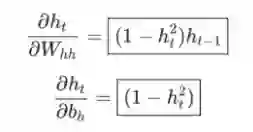
我们需要的最后一件事是∂y/∂h_t。 我们可以递归地计算:

我们将从最后一个隐藏状态开始实现BPTT,所以当我们想要计算∂y/∂h_t时,我们已经有了∂y/∂h_{t+1}! 例外的是最后一个隐藏状态,h_n:
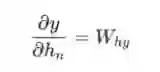
我们现在拥有了最终实现BPTT和backprop()所需的一切:

有几点需要注意:
为方便起见,我们将∂L/∂y*∂y/∂h合并为∂L/∂h。
我们不断更新一个包含最新∂L/∂h_{t+1}的d_h变量,我们需要计算它的∂L/∂h_t。
在完成BPTT之后,我们使用np.clip()去除梯度值低于-1或高于1的值.这有助于缓解爆炸梯度问题,即由于具有大量乘法项而使梯度变得非常大。 梯度爆炸或消失对于传统RNN来说是相当成问题的 ,像LSTM这样的更复杂的RNN通常能够更好地处理它们。
计算完所有梯度后,我们使用梯度下降更新权重和偏差。
我们做到了! 我们的RNN已经完成。
验证
07
这是我们等待的那一刻 ——让我们测试我们的RNN!
首先,我们将编写一个函数来帮助我们的RNN处理数据:
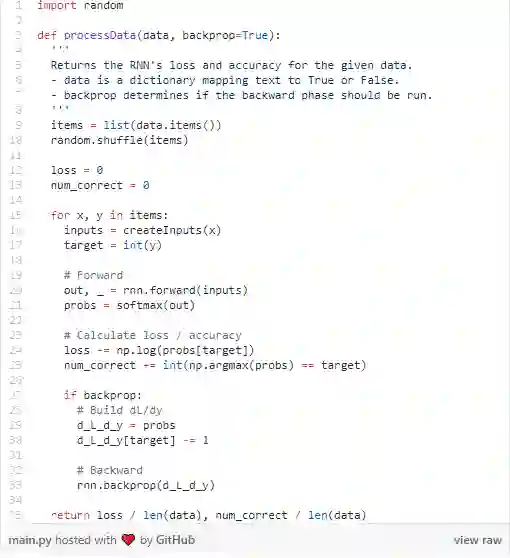
现在,我们可以编写循环训练的部分:

运行main.py应输出如下内容:

我们自己构造的RNN效果不错。
尾声
08
在这篇文章中,我们完成了递归神经网络的演练,包括它们是什么,它们如何工作,为什么它们有用,如何训练它们以及如何实现它们。 不过,你还可以做更多的事情:
了解长期短期记忆(LSTM)网络,一种功能更强大且更受欢迎的RNN架构,或关于门控再生单元(GRU),这是众所周知的LSTM变体。
使用适当的ML库(如Tensorflow,Keras或PyTorch)尝试更大/更好的RNN。
了解双向RNN,它可以处理前向和后向序列,因此输出层可以获得更多信息。
尝试像GloVe或Word2Vec这样的Word嵌入,可用于将单词转换为更有用的矢量表示。
查看自然语言工具包(NLTK),这是一个用于处理人类语言数据的流行Python库。
原文链接:https://victorzhou.com
项目地址:
https://github.com/vzhou842/rnn-from-scratch
-END-
专 · 知
专知,专业可信的人工智能知识分发,让认知协作更快更好!欢迎登录www.zhuanzhi.ai,注册登录专知,获取更多AI知识资料!
欢迎微信扫一扫加入专知人工智能知识星球群,获取最新AI专业干货知识教程视频资料和与专家交流咨询!
请加专知小助手微信(扫一扫如下二维码添加),加入专知人工智能主题群,咨询技术商务合作~

专知《深度学习:算法到实战》课程全部完成!550+位同学在学习,现在报名,限时优惠!网易云课堂人工智能畅销榜首位!
点击“阅读原文”,了解报名专知《深度学习:算法到实战》课程