【博士论文】关于经典变量、对易与量子版本洛瓦兹局部引理的研究

来自中科院计算所何昆的博士论文，入选2020年度“CCF优秀博士学位论文奖”初评名单！

https://www.ccf.org.cn/Focus/2020-12-03/717578.shtml

关于经典变量、对易与量子版本洛瓦兹局部引理的研究

洛瓦兹局部引理，也简称局部引理，是组合数学和概率论中一种强有力的工 具，它可以用来证明，当一系列“坏事件”满足一定的概率约束和“弱相关”约束 时，可以同时避开所有的坏事件。在最近十年，局部引理因为算法化方面的工作 以及向量子领域的扩展，又重新得到了理论计算机界的大量关注。目前领域内存 在着不同版本的局部引理，主要有抽象版本，变量版本，对易版本和量子版本。这些局部引理有各自的应用。抽象版本局部引理是最经典的局部引理，Shearer 首先给出了抽象版本局部引理的紧的条件。变量版本局部引理假设事件由一系 列独立的随机变量决定，尽管变量版本局部引理涵盖了局部引理的绝大多数应 用，但人们对变量版本局部引理的紧的条件却知之甚少。2009 年，Ambainis 等 人引入了量子版本局部引理，该引理是研究量子可满足性问题的强有力工具。量 子版本局部引理的紧的条件也是未知的。还有人研究对易版本局部引理，相关研 究主要集中在对易版本局部引理的算法化上，目前还没有对其紧的条件的研究。

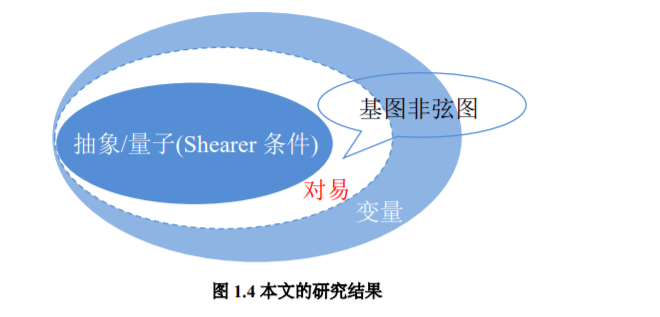
第一，我们从数学上刻画了变量版本局部引理紧的条件，并证明了变量版本 局部引理同抽象版本是不同的，解决了 Szegedy 提出的开放问题。基于该条件， 我们得到了两类很重要的事件-变量图，即树和圈的边界刻画，这是变量版本局 部引理的边界首次在某类非平凡的二部图上被刻画清楚。我们还给出了变量版 本局部引理同抽象版本有差异的充分必要条件。基于这一条件，我们得到了很多 变量版本与抽象版本有差异与无差异的例子。

第二，我们证明了 Shearer 条件对量子版本局部引理是紧的，即最小的未被 覆盖的子空间的相对维度完全由独立集多项式刻画。从而解决了 Sattath 等人的 猜想，证明了 Gilyen 和 Sattath 的算法是紧的，同时还揭示了在 qudit 维度足够大 时几乎所有局域哈密尔顿量的量子可满足性问题都由晶格气模型的配分函数刻 画。

第三，我们证明了对易版本局部引理同量子版本（或抽象版本）是不同的。同时，我们还给出了在给定 qudit 维数的情况下，树的对易版本局部引理紧的条 件。该结果意味着，对于对易的局域哈密尔顿量，原则上可以设计出在 Shearer 界之外依然高效的算法。

https://www.ccf.org.cn/ccf/contentcore/resource/download?ID=143742

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“局部引理” 就可以获取《【博士论文】关于经典变量、对易与量子版本洛瓦兹局部引理的研究》专知下载链接

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源