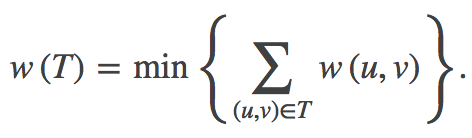Prim 算法及其高效实现

会员服务 ·

Prim 算法及其高效实现

2018 年 3 月 29 日 算法与数据结构

来自：ivy-end

http://www.ivy-end.com/archives/943

背景

最小生成树（Minimum Spanning Trees），简称MST。是图论中一个非常重要的概念。解决这个问题有两种算法，今天暂且先来讨论一下Prim Algorithm。不做特别说明，讨论的都是无向图。

首先介绍一下最小生成树的概念，我们知道，图可以这样定义 G=(V,E) ，其中 G 表示图，V 表示顶点集合，E 表示边集合。最小生成树是这样一棵树，它满足：

通俗地讲，就是使得图GG连通时，所选取的边的长度的和最小。

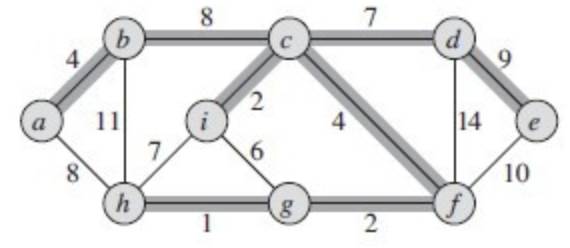
如上图，加粗的路径就是在最小生成树上的路径。

算法讲解：

现在，我们开始讨论Prim Algorithm。这个算法可以分为下面几个步骤：

将顶点集 V 分成两个集合 A 和 B，其中集合 A 表示目前已经在MST中的顶点，而集合 B 则表示目前不在 MST 中的顶点。

寻找与集合 A 连通的最短的边 (u,v)，将这条边加入最小生成树中。（此时,与(u,v) 相连的顶点，不妨设为 Bi，也应加入集合 A 中）重复第二步，直至集合 B 为空集。

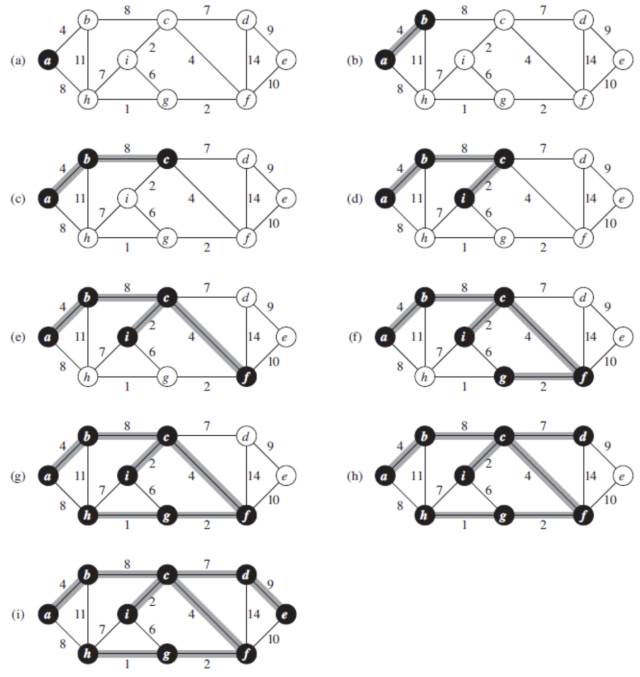
算法的大体思想就是这样了。为了方便理解，我们先来看一下下面一张图片：

对照上面的图片，想必对于Prim Algorithm也有了一定的理解。

下面我们来设计算法，显然，我们需要遍历集合 A 中所有顶点及与之相连的边，取连接到集合B的权值最小的边，加入最小生成树。这样一来，复杂度将达到 O(n3)。

我们可以对这个想法进行优化。我们维护一 pCost[i] 数组，用来表示从集合A到与之相邻的节点的最小费用。这样，我们只要每次取这个数组中的最小值，把它在集合B中所对应的结点Vi加入到集合A中。

每次加入结束以后，都要更新pCost[i]数组。即枚举所有与结点Vi相连的边，判断是否比pCost[i]数组中的最小费用小，如果比它小，则更新。这样可以将算法优化到O(n2)。

代码如下：

#include <iostream>

#include <memory.h>

#include <vector>

using namespace std;

const int MAX = 1024;

const int INF = 2147483647;// 设置最大权值

int N, M;

vector<pair<int, int> > pMap[MAX];// 邻接表

void Prim();

int main()

{

cin >> N >> M;

for(int i = 1; i <= M; i++)

{

int u, v, w;

cin >> u >> v >> w;

pMap[u].push_back(make_pair(v, w));

pMap[v].push_back(make_pair(u, w));

}

Prim();

return 0;

}

void Prim()

{

int nCost = 0;

vector<int> pMST;// 储存MST的结点

int pCost[MAX];// 储存与集合A相邻的顶点的最小权值，0表示该结点已经在MST中

pMST.push_back(1);// 将结点1加入MST

pCost[1] = 0;

for(int i = 2; i <= N; i++)// 初始化，切记要将除1以外的都置为INF

{ pCost[i] = INF; }

for(int i = 0; i < pMap[1].size(); i++)// 处理与结点1相连的顶点

{ pCost[pMap[1][i].first] = pMap[1][i].second; }

for(int i = 1; i <= N - 1; i++)// 剩余N-1个顶点，循环N-1次

{

int nVertex = 0, nWeight = INF;// 用于寻找最短的边

for(int j = 1; j <= N; j++)

{

if(nWeight > pCost[j] && pCost[j] != 0)

{

nVertex = j;

nWeight = pCost[j];

}

}

pCost[nVertex] = 0;

pMST.push_back(nVertex);// 将节点nVertex加入MST

nCost += nWeight;// 计算MST的费用

for(int j = 0; j < pMap[nVertex].size(); j++)// 更新pCost数组

{

if(pCost[pMap[nVertex][j].first] != 0 &&

pCost[pMap[nVertex][j].first] > pMap[nVertex][j].second)

{

pCost[pMap[nVertex][j].first] = pMap[nVertex][j].second;

}

}

}

cout << "MST Cost is " << nCost << endl;

cout << "The vertexs in MST are ";

for(int i = 0; i < pMST.size(); i++)

{ cout << pMST[i] << " "; }

cout << endl;

}