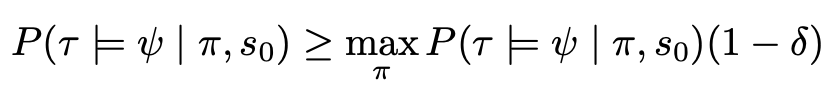走向通用人工智能之路，世界模型为何不可或缺？

摘要

世界模型是灵活的目标导向行为的必要因素，还是无模型学习就足够了？我们对这个问题给出了正式的答案，表明任何能够泛化到多步目标导向任务的智能体都必须已经学习到了其环境的预测模型。我们证明了可以从智能体的策略中提取出这个模型，并且提高智能体的性能或其能够达成的目标的复杂性需要学习越来越精确的世界模型。这带来了诸多影响：从开发安全且通用的智能体，到界定复杂环境中智能体的能力，以及提供从智能体中获取世界模型的新算法。

关键词：世界模型 (world model)、模型无关学习 (model-free learning)、目标条件策略 (goal-conditioned policy)、后悔界 (regret bound)、环境预测 (predictive model)、线性时序逻辑 (Linear Temporal Logic)********************************

彭晨丨作者

论文题目：General agents need world models 发表时间：2025年6月2日论文地址：https://arxiv.org/abs/2506.01622 论文会议：ICML 2025 **

背景

近年来，随着少样本（few-shot）与零样本（zero-shot）学习在大语言模型中的突破，人们对通用智能体（general agents）是否必须构建“世界模型”展开了激烈争论。一方面，纯粹的无模型学习（model-free learning）已在诸多任务中展现出惊人泛化能力；另一方面，心理学与认知科学则强调人类在进行多步规划时依赖丰富的环境表征（world models）。本文由Richens等人正式回答了这一问题：任何能够在多步目标导向任务上保持较低后悔（regret）的智能体，都必然学会了环境的预测模型。

人类智能与世界模型

人类可以凭借心智表征预演未来、设定抽象目标，进而在从未见过的场景中灵活行动。这些“世界模型（world models）”早在1983年就被提出[1]，用以解释我们如何从感官输入中跳脱出来，进行主动规划。然而，在机器学习领域，Brooks等人曾宣称“世界即模型”，纯粹依赖感知-动作循环的模型无关智能体同样能够涌现出智能行为。本文在此争论框架下出发，给出了一个严谨的数学答案。

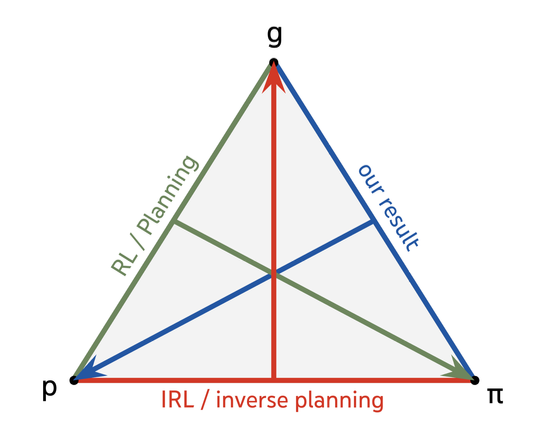
图 1. 本文的结果补充了之前关于规划和逆向RL的见解。规划使用世界模型和目标来确定策略，逆向RL和逆规划使用智能体的策略和世界模型来确定其目标，而本文使用智能体的策略和目标来确定世界模型。

问题描述：受控马尔可夫过程与目标条件策略

研究者将环境形式化为受控马尔可夫过程（controlled Markov process），只包含状态空间 S、动作空间 A 以及转移函数Pss'(a)，未指定奖励或折扣。智能体被定义为一类“目标条件策略”（goal-conditioned policy），即策略π(at|ht;Ψ)同时依赖历史ht和用户指定的复合目标Ψ。为了对比不同目标复杂度，对“复合目标”引入线性时序逻辑（Linear Temporal Logic, LTL），将单步目标（Now/Next/Eventually）和子目标序列（sequential goals）、或并组合（disjunction）纳入统一框架。

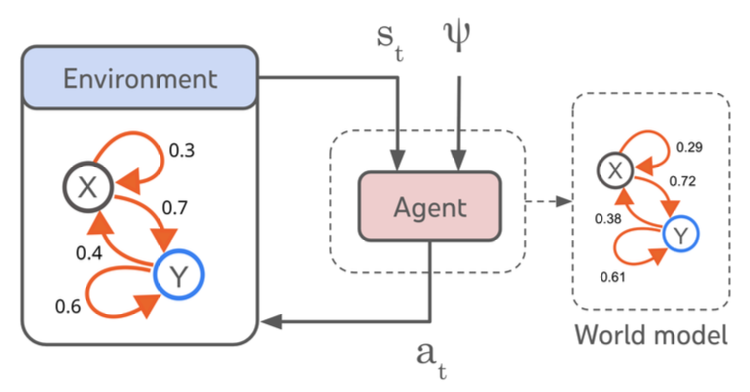
图 2.智能体-环境系统。智能体是从状态st（或历史）和目标ψ到动作at的映射。

核心理论：后悔界与世界模型的等价性

对任何一个有限深度 n 的复合目标集合 Ψₙ，若一个策略 π 能够在所有 ψ∈Ψₙ 上满足

即保持最大策略的 1–δ 成绩（δ为后悔界），则可以从该策略本身精确地“回收”出一个转移函数近似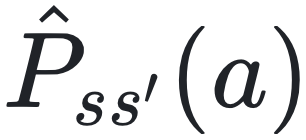。研究证明：随着目标深度 n 增大、或后悔界 δ→0，近似误差以 O(δ/√n)+O(1/n) 速度收敛于 0。这一结果表明，若智能体能在多步长进程目标上保持较低后悔水平，就必然学到了环境的预测模型，二者在信息论上等价。

算法实践：从策略抽取环境模型

基于上述定理，作者进一步设计了一个无监督且通用的世界模型回收算法。该算法仅与策略 π 和目标生成器交互，不依赖智能体内部网络激活或对环境的额外访问。它构造一系列“互斥子目标”ψ₁∨ψ₂，统计策略 π 在不同时刻对两者的选择概率，通过二项分布中位数的猜测反演出转移函数Pss'(a)的估计值，并以理论界限保证估计误差。

实验验证：模型精度随任务深度演进

在一组随机生成的 20 状态、5 动作受控马氏过程环境中，研究训练了多批智能体，并测量它们对不同目标深度 ψ 的平均后悔⟨δ⟩。结果显示，即使这些智能体在某些目标上后悔达 1（完全失效），只要它们对深度 n 目标在平均后悔 ⟨δ⟩ 水平较低，算法依然能以 ∼O(n⁻¹ᐟ²) 速率回收高精度环境模型。这一实证验证了定理的鲁棒性：即便严格假设不完全满足，策略中隐含的“世界模型”依然可提取。

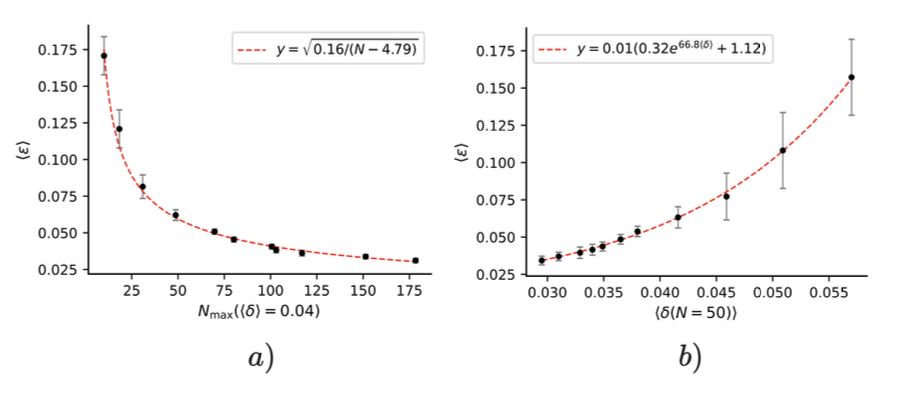
图 3. a) 根据算法重建的世界模型中的平均误差， ⟨λ⟩，随着智能体学习推广到更高深度的目标而减少。B)⟨δ(n= 50)⟩的平均误差缩放，智能体为深度n= 50个目标实现的平均后悔。

深度讨论：模型学习的多重意义

本文的理论与实证结果带来多重启示：首先，无模型通向通用智能之路并不存在——任何长期目标泛化都要求模型学习，否则后悔将不可避免；其次，隐式世界模型或许正是大规模语言模型等“基础模型”（foundation models）中涌现能力的根本机制；再次，对安全与可解释性的需求也因而得到理论保障：我们可从“黑箱”策略中提炼出预测模型，用于计划验证与风险评估；最后，定理反转了“好调节者定理”（Good Regulator Theorem），不仅展示剂对环境的最优控制暗示模型存在，也给出了可构造回收映射。

拥抱世界模型，迈向通用智能

研究从信息论视角正式回答了“通用智能体是否需要世界模型”的基础问题：要想在多步复杂目标中保持低后悔，就必须学会环境转移函数的近似，二者在本质上等价。未来，通用人工智能研究应正视世界模型学习的挑战与价值，不再将其视作可选项，而是通向可靠性、效率与可解释性的核心路径。

如果你对大模型可解释性的话题感兴趣，欢迎你报名集智最近策划的「破解AI黑箱的四重视角：大模型可解释性读书会」，详情见文末。

参考文献：