【CVPR2024】MoReVQA:探索视频问答的模块化推理模型

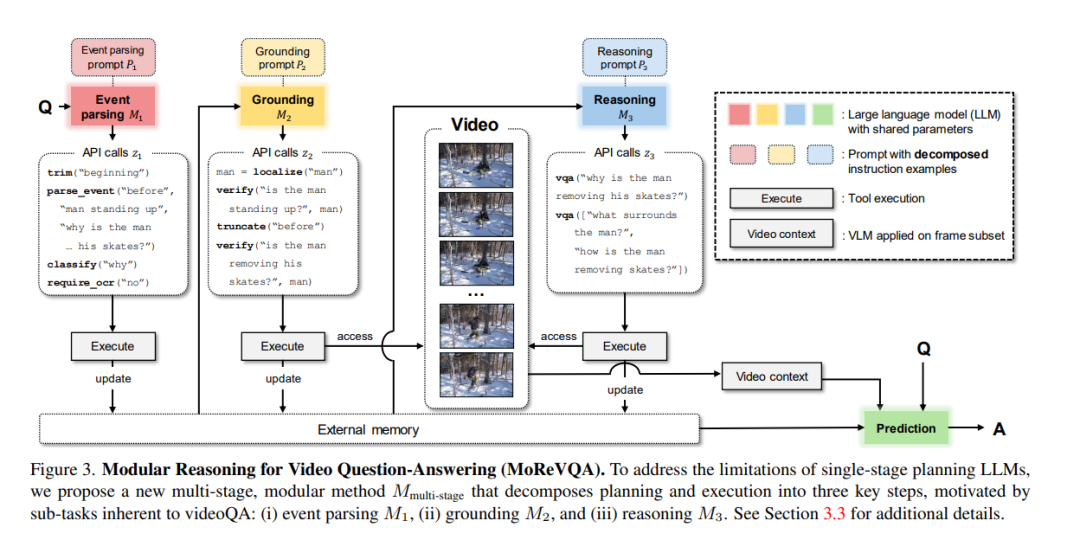
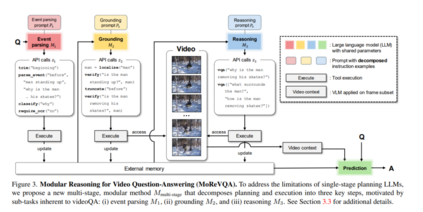
本文通过一个分解的多阶段、模块化推理框架来解决视频问答（videoQA）任务。以往的模块化方法已经在视觉内容未涉及的单一规划阶段显示出潜力。然而，通过一个简单有效的基线，我们发现这样的系统在实践中对于具有挑战性的视频问答设置可能导致脆弱的行为。因此，与传统的单阶段规划方法不同，我们提出一个包括事件解析器、基础阶段和最终推理阶段以及外部存储的多阶段系统。所有阶段都无需训练，并通过大模型的少数次提示进行，每个阶段都产生可解释的中间输出。通过分解基础规划和任务复杂性，我们的方法MoReVQA在标准视频问答基准（NExT-QA、iVQA、EgoSchema、ActivityNet-QA）上超越了以往的工作，取得了最新的成果，并扩展到相关任务（基于视频的问答、段落标题生成）。