《导弹规避的优化控制方法》200页论文

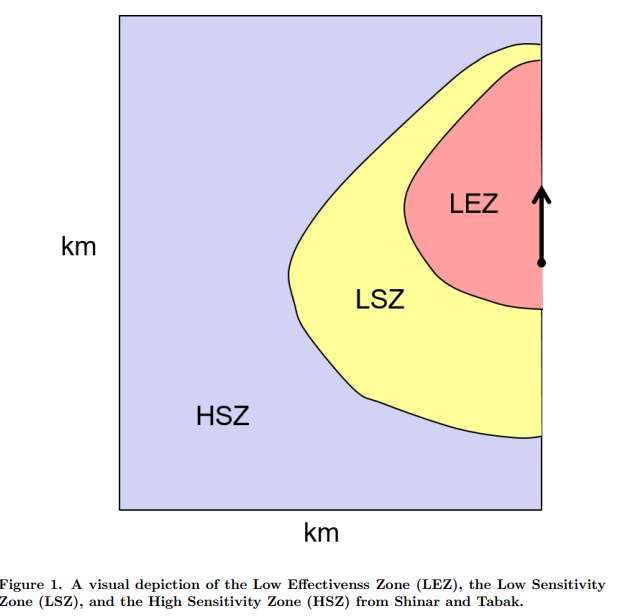
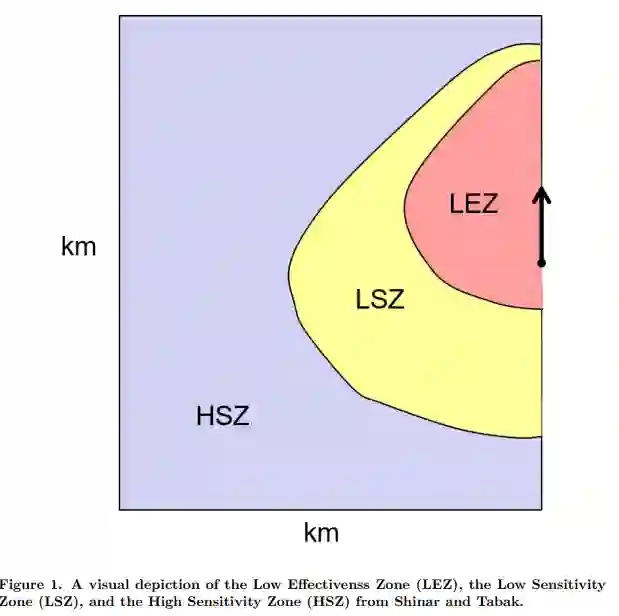
最优控制理论被应用于导弹规避的研究，特别是在单个追击导弹与单个规避飞机的情况下。建议将规避问题分为两个阶段，分别以能量和机动性为主要考虑因素。在机动性阶段使用的传统规避战术有据可查。为了表示以能量管理为主导的第一阶段，最优控制问题可以从两个方面提出：一个是以最大化躲避者与追击者之间的最终距离为目标的固定最终时间问题；另一个是以最大化导弹与躲避者之间达到一定捕获距离时的最终时间为目标的自由最终时间问题。

这两个最优控制问题是在关于追击者假设的几种不同情况下进行研究的。首先，对追击者采用次优控制策略，即比例导航。其次，假设追逐者的行为是最优的，这就要求解决一个双面最优控制问题，也就是所谓的微分博弈。由此得出的轨迹称为最小最大值，可以证明它考虑了追逐者控制策略的不确定性。最后，在 "后退地平线控制 "和 "实时最优控制 "的背景下研究了运动和状态都不确定的追逐者。结果凸显了更新最优控制轨迹如何降低所产生的错过距离的不确定性。