时间序列预测的全面综述：架构多样性与开放挑战

时间序列预测是一个至关重要的任务，它为经济规划、供应链管理和医学诊断等各个领域的决策提供了关键信息。过去，传统统计方法和机器学习曾被广泛应用于时间序列预测问题，然而，随着多种基础的深度学习架构如多层感知机（MLP）、卷积神经网络（CNN）、递归神经网络（RNN）和图神经网络（GNN）的发展，这些架构被逐步应用于时间序列预测问题的解决。然而，由于每种深度学习架构的归纳偏置所带来的结构性限制，它们的性能也受到了制约。变换器模型（Transformer），擅长处理长期依赖关系，已经成为时间序列预测中的重要架构组件。然而，近期的研究表明，简单的线性层等替代方案能够超越变换器模型。这些发现为使用多样化架构提供了新的可能性。在探索各种模型的背景下，时间序列预测的架构建模已经进入了一个复兴阶段。本综述不仅为时间序列预测提供了历史背景，还对向架构多样化发展的趋势进行了全面而及时的分析。通过比较和重新审视多种深度学习模型，我们揭示了新的视角，并呈现了时间序列预测中的最新趋势，包括混合模型、扩散模型、Mamba模型和基础模型的出现。通过聚焦时间序列数据的内在特性，我们还讨论了时间序列预测中受到关注的开放挑战，如通道依赖性、分布变化、因果关系和特征提取等。本综述探讨了通过多样化方法提升预测性能的关键要素。这些贡献有助于降低新入门者进入时间序列预测领域的门槛，同时为经验丰富的研究者提供了广阔的视野、新的机会和深刻的见解。 关键词：时间序列预测，深度学习，基础模型，分布变化，因果关系

1 引言

时间序列预测（Time Series Forecasting, TSF）是一个基于历史数据序列预测未来值的任务（Cryer, 1986）。它作为各个领域的关键决策工具，广泛应用于经济与金融、供应链管理、交通运输、能源、气象和医疗保健等领域（Danese 和 Kalchschmidt, 2011；Abu-Mostafa 和 Atiya, 1996；Alghamdi 等, 2019；Nti 等, 2020；Dimri 等, 2020；Soyiri 和 Reidpath, 2013）。这些应用提供了诸多机会，包括降低成本、提高效率和增强竞争力（Danese 和 Kalchschmidt, 2011）。然而，时间序列数据固有的多样性和复杂性使得预测变得极具挑战性。除了显而易见的信息外，各种隐藏的模式使得学习时间依赖关系变得更加困难，而在某些时候不规则的值进一步加剧了这一问题。在多变量问题中，诸如通道相关性等额外因素使得任务变得更加复杂（见第2.1节）。此外，时间序列数据因领域的不同而展现出不同的特征，数据采集的时间和环境也导致了显著不同的模式（见第2.3节）。因此，TSF问题通常具有有限的模型泛化能力，需要多样化的架构和方法。日益复杂的TSF问题给研究人员带来了更大的挑战，近期这也促使了新方法和算法的积极发展，以应对这些问题（Lim 和 Zohren, 2021）。

在主要的人工智能和机器学习会议上接受的论文数量急剧增加（见图2），证明了TSF研究在人工智能和机器学习领域的重要性不断上升。随着越来越多的研究致力于解决时间序列预测问题，综述性论文也频繁发表（见表1）。随着时间的推移，许多综述性论文系统地整理了TSF的广泛领域，提供了深入的研究，给研究人员提供了宝贵的指导和方向。然而，现有的综述论文仍有改进的空间，特别是在应对模型多样性日益增加和领域中的开放挑战方面。

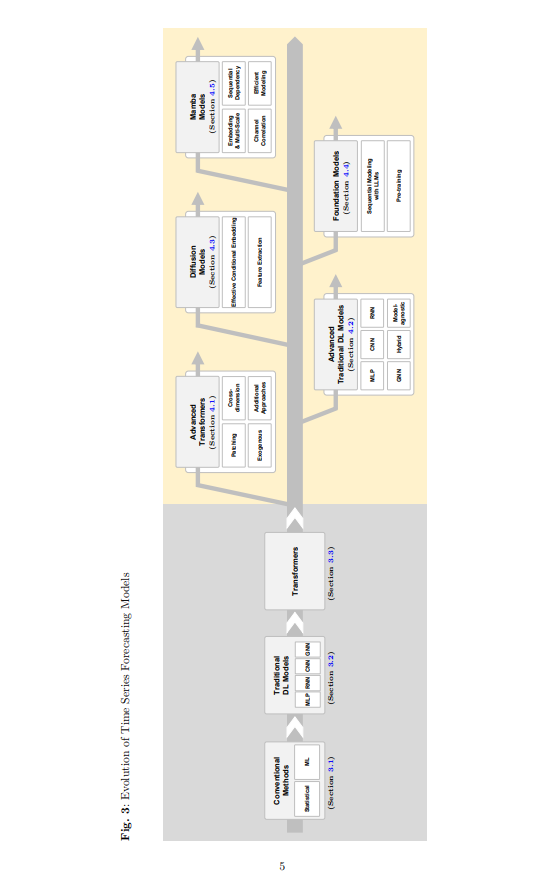
TSF模型经历了长时间的发展。过去，主要使用基于移动平均的统计方法，后来发展成了传统方法，如指数平滑和自回归综合滑动平均（ARIMA）（Bartholomew, 1971）。机器学习技术，如决策树模型（Quinlan, 1986）和支持向量机（SVM）（Cortes, 1995），也曾被广泛应用，但它们在学习复杂的非线性模式方面存在局限性（见第3.1节）。随着可用数据量的增加和硬件计算能力的提升，各种深度学习架构如多层感知机（MLP）（Rumelhart 等, 1986）、递归神经网络（RNN）（Hopfield, 1982）、卷积神经网络（CNN）（LeCun 等, 1998）和图神经网络（GNN）（Scarselli 等, 2008）被开发出来，能够学习更复杂的模式。然而，这些早期的深度学习架构的性能受限于它们的内在设计。为了克服这些结构性限制，像长短期记忆网络（LSTM）（Hochreiter 和 Schmidhuber, 1997a）和时序卷积网络（TCN）（Bai 等, 2018）等变种被广泛应用（见第3.2节）。变换器（Transformer）（Vaswani, 2017）因其处理长期依赖关系的能力，在自然语言处理领域表现出色，随后也自然地扩展到时间序列数据。尽管变换器在TSF中表现良好并且广泛流行，但近期的研究表明，简单的线性模型也可以超越变换器模型（见第3.3节）。因此，重新审视传统深度学习方法的兴趣显著增加，并且对各种架构（如基础模型、扩散模型和Mamba模型等）产生了越来越多的关注（见第4.2、4.3、4.4、4.5节）。变换器模型仍在持续改进，并在TSF中扮演着重要角色（见第4.1节）。因此，TSF进入了一个建模的复兴阶段，各种方法正在积极竞争，且没有任何单一方法占据主导地位（见图3）。在这种背景下，本综述具有两个主要优点，使其与以往的TSF综述论文区别开来。

首先，我们关注架构多样性的不可避免性，提供了一个及时和全面的视角，帮助理解当前架构多样化的趋势。现有的TSF综述论文，如（Wen 等, 2022a；Zhang 等, 2024c；Lin 等, 2024a；Meijer 和 Chen, 2024；Patro 和 Agneeswaran, 2024a），主要集中在对特定架构的详细分析，但在广泛比较多样化架构，包括新兴架构方面存在局限性。本论文系统地比较了各种架构（MLP、CNN、RNN、GNN、Transformer、扩散模型、基础模型、Mamba）的发展进展，并分析了每种架构的优缺点和贡献。此外，本文还探讨了结合多种架构优点的混合模型的性能，清晰地展示了TSF中的关键趋势。通过这些贡献，读者能够有效地理解该领域不断发展的趋势和方向。通过这一方式，它降低了新入门者进入TSF领域的门槛，并为经验丰富的研究人员提供了广阔的视野和新的研究机会。

其次，我们从开放挑战的角度进行探讨。尽管许多先进的架构已经解决了许多问题，但TSF中的核心挑战仍然存在。特别是，通道相关性、分布变化、因果关系和特征提取等问题（见第5节）依然是需要解决的重要挑战（见图4）。本综述探讨了旨在解决这些挑战的最新方法，并为读者提供了宝贵的解决问题的见解。尽管先前的综述提供了有关开放挑战的有用视角，但它们在这些问题的探讨深度上有所不足。本综述旨在弥补这一空白，提供更为全面的分析并提出新的解决方案。 本综述首先介绍了时间序列数据的基本概念和预测问题定义（第2节），然后回顾了过去方法的发展历程（第3节）。在第4节中，分析了最新模型的关键特征，最后在第5节中，探讨了TSF中的开放挑战及其解决方案。通过这些内容，读者将获得对TSF研究过去和现在的广泛理解，并为未来的研究提供新的思路。