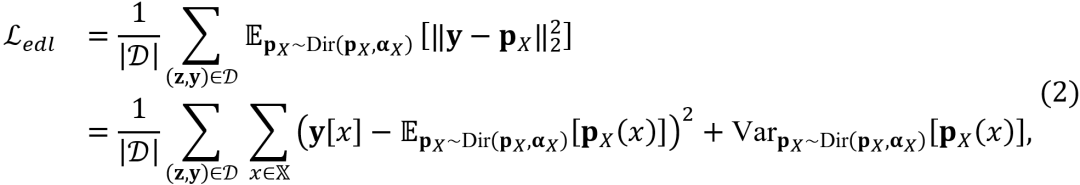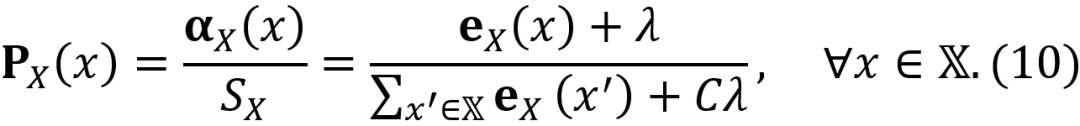证据深度学习是一种新兴的不确定性估计算法,可以在几乎不增加额外计算量的前提下得到可靠的不确定性估计。本文提出了名为Relaxed-EDL的扩展算法,重新审视并放宽了传统证据深度学习方法中的若干非必要设置,在多个不确定性估计任务上取得了优异性能,被ICLR2024接收为Spotlight工作。
**
论文标题:R-EDL: Relaxing Nonessential Settings of Evidential Deep Learning 论文作者:陈孟沅,高君宇,徐常胜 作者单位:中国科学院自动化研究所 论文链接: https://openreview.net/pdf?id=Si3YFA641c 代码链接: https://github.com/MengyuanChen21/ICLR2024-REDL
摘要 一种新兴的不确定性估计方法——证据深度学习(Evidential Deep Learning,简称EDL),能够在单次前向传播中获得可靠的预测不确定性,因此受到了越来越多的关注。在主观逻辑理论的指导下,EDL 从深度神经网络中获得狄利克雷浓度参数,从而构建狄利克雷概率密度函数,以建模类别概率的分布。尽管已经取得了巨大成功,我们认为EDL在模型构建和优化的两个阶段都仍然保留了一些非必要的设置。在构建狄利克雷概率密度函数时,有一个常被忽略的先验权重参数,在利用证据比例和其大小来推导预测分数之间起到了平衡作用。在模型优化时,传统EDL采用的最小化方差正则项会促使狄利克雷概率密度函数逼近狄拉克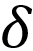
01
- 引言 在高风险领域,如自动驾驶和医学分析中,模型能够可靠地传达其预测置信度是至关重要的 [1-2]。然而,先前的研究表明,大多数现代深度神经网络,尤其是通过监督学习进行分类训练的网络,普遍表现出较差的校准能力,倾向于给出过度自信的预测结果 [3]。尽管目前已经开发出了基于贝叶斯理论和集成技术的不确定性量化方法,这些主流方法在推理阶段都需要多次前向传播 [4-9],从而带来了大量的计算开销,阻碍了在工业界的广泛应用。这个限制促使研究人员们继续探索如何在尽量少的额外成本下实现高质量的不确定性估计。 证据深度学习(Evidential deep learning,简称EDL)[10]是一种新兴的单次前向传播不确定性估计方法,由于其在各种模式识别任务中的成功[11-19],已经引起了人们越来越多的关注。基于主观逻辑理论[20-21],EDL利用类间收集到的证据比例及其幅值来实现高质量的不确定性估计,可以有效缓解模型在误分类和分布外样本上的过度自信。具体来说,在C类任务中,EDL 构建了一个狄利克雷分布
来在主观逻辑的指导下对类概率的分布进行建模,浓度参数由以下公式给出:
其中,先验分布 通常设为
上的均匀分布,其标量系数C作为一个参数称为先验权重。随机变量X表示输入样本的类别索引,
表示样本与类别相关的收集证据。随后,为了优化模型,传统的EDL方法在假设类概率
服从上述狄利克雷分布的基础上,结合类概率
上的均方误差(MSE)损失,得出优化目标为:
其中,训练集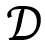
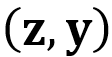
的MSE损失的积分的优点。通过弃用最小化方差的正则项来放宽EDL优化目标已被证明可以缓解过度自信问题。 * 在多个不确定性估计任务上进行了广泛实验,包括置信度估计和分布外检测,全面展示了我们提出的 R-EDL 的有效性,并在经典、小样本、带噪等设置下表现出显著的性能。
02
- 主观逻辑理论 正如二值逻辑和概率逻辑的名称所暗示的那样,二值逻辑中的命题必须是真或假中的一种,而概率逻辑中的命题可以取值为 [0,1] 范围内的概率,以表达部分为真的含义。此外,主观逻辑[20–21]通过明确包含对概率的不确定性来扩展概率逻辑。具体来说,主观逻辑中的命题,也称为主观意见,被形式化如下:
分配给x的信念质量表示对x为真的支持,不确定性质量可以解释为分配给整个域的信念质量。因此,主观逻辑通过根据先验分布将不确定性质量重新分配到域内的每个单个值,从而提供了一个符合传统概率理论加法要求的投影概率,如下所示:
此外,主观逻辑理论指出,如果给定先验分布和称为先验权重的参数W,则多项式意见与狄利克雷概率密度函数之间存在双射。这种关系源于通过概率密度解释二阶不确定性,并在主观逻辑中发挥重要作用,因为它提供了利用概率密度函数的计算推理方式。
03
- R-EDL:通过放宽EDL中的非必要设置来缓解过度自信 尽管EDL及其相关工作取得了显著成功,我们认为现有的EDL方法(第3.1节)在狄利克雷分布的构建上(定理1)和优化目标的设计上保持了一些死板的设置,这些设置虽然被广泛接受,但并不是主观逻辑框架(第2节)本质上所要求的。本节的理论分析和第5节的实验均表明,这些非必要的设置阻碍了该类方法更准确地量化不确定性。具体来说,本节我们仔细分析并放宽了EDL中的两种非必要设置,包括:(1)在模型构建中,先验权重参数被固定为类别数(第3.2节);(2)在模型优化中,传统的优化目标包含一个最小化方差的正则项,这可能会加剧过度自信(第3.3节)。需要注意的是,我们对上述EDL非必要设置的放宽都是严格遵循主观逻辑理论的。
3.1****预备知识:证据深度学习
基于主观逻辑理论,[10] 提出了一种名为证据深度学习(EDL)的仅需单次前向传播的不确定性估计方法,该方法使深度神经网络充当分析员的角色,提供样本的信任质量和不确定性质量。例如,在C类分类的情况下,输入样本的信任质量 和不确定性质量
,其类别索引为随机变量X的取值x,具体定义如下:
其中,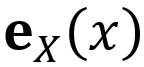
. 为了进行模型优化,EDL假设类概率服从双射中指定的狄利克雷概率密度函数,并整合了传统的均方误差损失函数,从而得出等式2所示的优化目标。在推理中,EDL利用投影概率(参见定义2)作为预测得分,并使用等式5计算分类不确定性作为不确定性质量
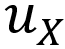
**
**
3.2 放松模型构建中先验权重的固定设置 在本小节中,我们阐明了先验权重W如何在利用证据的比例和大小来计算预测得分之间调整平衡。我们反对W将固定为类别数量的设置,并提出可以将其视为一个可调节的超参数。 先验权重的命名源自于等式1的表达式。这里,作为先验权重的标量系数C表示先验分布的权重。在定理 1 中,应该注意到双射的存在依赖于某些前提条件;即必须提供先验分布和先验权重。通常,在没有先验信息的情况下,我们默认将先验分布设置为域上的均匀分布。 然而,先验权重的设置是值得进一步讨论的。 我们认为将先验权重固定为域的基数(这是EDL研究者广泛采用的方法)并非主观逻辑所本质要求的,并且可能导致违反直觉的结果。例如,一个 100 类的分类任务中通常强制W=100,即使神经网络给出一个极端的证据分布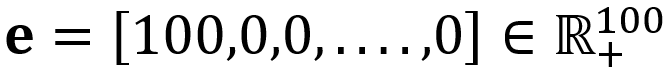
, 这显然是非常违反直觉的。上述现象的根本原因在于W的值事实上决定了投影概率受证据大小还是证据比例的影响程度。为了更清楚地阐明这一点,我们首先在不将先验权重固定为C的情况下重新审视等式 5 和等式 6。通过这种方式,我们可以得到投影概率的泛化形式,如下所示:
当先验权重W被设置为零时,等式 7 中的投影概率将退化为传统的概率形式,这种形式仅依赖于各类证据的比例,而不受证据大小的影响,因为将证据按常数系数缩放不会影响投影概率。然而,当W不为零时,我们有
等式 8 表明,在极端证据分布的情况下,即除了类别x之外的所有类别的证据均为零时,投影概率的上限由类别x证据与先验权重的比率决定。换句话说,当给定先验权重时,投影概率的上限纯粹依赖于 的大小,较小的证据大小会导致投影概率的上限和1之间的差距更大。 从上述两个情况可以看出,先验权重的值决定了投影概率分别受证据大小和比例影响的程度。具体来说,小的先验权重意味着投影概率主要受证据分布比例的影响,而大的先验权重则使投影概率主要考虑证据的大小而忽略证据的比例。 直观地说,对于任何特定情况,都应该存在一个先验权重的最佳值可以权衡利用证据比例和其大小,从而缓解模型对误分类和分布外样本的过度自信。然而,考虑到影响网络输出的复杂因素众多,这样的最佳值不太可能普遍地适用于所有情境。因此,我们建议放弃将类别数量分配给先验权重的死板做法,而是将先验权重视为神经网络中的一个可调节超参数。因此,我们重新审视等式4,从而推导出所构建的狄利克雷PDF的浓度参数的泛化形式:
其中 是一个超参数。值得注意的是,投影概率的形式与等式4中一致,但不确定性质量的表达式为
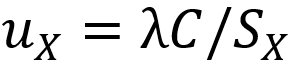
3.3 弃用模型优化中的最小化方差正则化
在前一小节中,我们强调了将先验权重视为可调超参数的重要性,这使得投影概率能够有效平衡利用收集证据的比例和大小。因此,在本小节中,我们阐明了我们优化目标背后的逻辑,该目标侧重于直接优化投影概率。通过与EDL中使用的传统损失函数进行比较,我们的方法抛弃了一个常用的最小化方差正则化项。我们仔细阐述了排除该项来放宽EDL优化目标的动机。在得到等式 9后,投影概率将具有以下变体:
因此,通过将传统均方误差损失中的类别概率替换为等式10中的投影概率,在放宽的EDL框架中可以无缝地推导出适当的优化目标
采用上述优化目标的原因,是我们认为投影概率可以减轻由优化到硬性独热标签而导致的过度自信问题。如前所述,投影概率利用了收集到的证据的大小和比例,以更准确地表示给定输出的实际可能性。从优化的角度来看,相对于类别间证据的比例,投影概率对不确定性质量的存在更具宽容性,因为根据先验分布,不确定性质量也对投影概率有所贡献。换句话说,当模型尚未收集到足够的证据时,项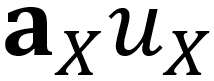
这可以由等式10和狄利克雷分布的性质推导得到。因此,通过将等式12代入等式11,再与等式2进行比较,我们可以发现这两个优化目标之间的本质区别在于:EDL优化的是传统MSE损失在构建的狄利克雷 PDF上的期望,而我们提出的R-EDL直接优化的是构建的狄利克雷PDF的期望的MSE损失。因此,试图最小化狄利克雷分布方差的正则化项 将被弃用,这一项的表示式如下:
我们可以更深入地探讨这个最小化方差的正则化项。当狄利克雷分布的方差接近于零时,狄利克雷概率密度函数将呈现为狄拉克 函数的形式,即无限高且薄。因此,在整个训练阶段,正则化项
会持续要求收集目标类别的无限大证据,这进一步加剧了我们试图缓解的过度自信问题。从另一个角度来看,当狄利克雷分布的方差接近于零时,用于建模一阶概率的狄利克雷分布将逐渐退化为传统的一阶概率点估计,从而失去在建模二阶不确定性时主观逻辑理论的优势。因此,我们认为忽略这个正则化项有助于缓解不确定性估计中的过度自信问题,同时保留主观逻辑的优点。我们的后续消融研究进一步证实了这一论断。
04
- 相关工作 EDL的扩展与应用:在第3.1节中可以找到对EDL的详细介绍,这里将简要介绍EDL的后续工作。在[10]提出EDL之后,深度证据回归 [11,23]通过将证据先验引入传统的高斯似然函数,扩展了这一范式,从而增强了回归网络中不确定性的建模。[24]结合EDL、神经过程和神经图灵机提出了证据调整过程(Evidential Tuning Process),该方法比EDL表现更强,但需要相当复杂的记忆机制。[25]进一步深入探讨了DER在不确定性参数过多表示情况下的经验有效性。最近,[22]提出的I-EDL通过引入费舍尔信息矩阵来衡量样本所携带证据的信息量,大大超过了EDL。在应用方面,DEAR[12]通过提出一种新颖的模型校准方法来规范EDL训练,在开放集动作识别中取得了令人印象深刻的表现。此外,EDL在计算机视觉的其他应用中也取得了巨大成功[13,15,18,26,28]。与之前的工作相比,我们的方法是第一个在严格遵循主观逻辑理论的同时,考虑放宽传统EDL的非必要设置的方法。
基于DNN的其他单模型不确定性方法: 除了EDL相关的工作外,还有各种单模型方法用于估计预测不确定性。高效集成方法[5–8]将一组模型整合在一个模型下,在大规模数据集上表现出最先进的性能。虽然这些方法在参数上高效,但在推理过程中需要多次前向传播。贝叶斯神经网络(BNNs)[29–30]将网络参数建模为随机变量,并通过后验估计来量化不确定性,但其计算成本显著。一种广为人知的方法是蒙特卡洛Dropout[6],它将dropout层解释为服从伯努利分布的随机变量,训练包含此类dropout层的神经网络可以视为对变分推理的近似。另两个著名的单次前向传播方法,DUQ[31]和SNGP[32],通过使用径向基函数或高斯过程引入了距离感知的输出层。尽管在OOD基准测试中可与深度集成方法相媲美,但这些方法需要对训练过程进行深度修改,难以轻松地融合进现有分类器。另一组高效的不确定性方法是基于狄利克雷的不确定性(DBU)方法,EDL也属于这一类。突出的DBU方法包括KL-PN[33]、RKL-PN[34]和Posterior Network[35],它们在狄利克雷分布的参数化和训练策略上各有不同。与这些前述方法相比,我们的方法结合了表现优异、单次前向传播、参数高效和易于使用的优点。
05
- 实验 5.1 比较方法
根据 [22],我们重点与其他基于狄利克雷的不确定性方法进行比较,包括传统的EDL[10]、I-EDL [22]、KL-PN [33]、RKL-PN [34] 和 PostN [35]。此外,我们还展示了有代表性的单前向传播方法DUQ [31] 和流行的贝叶斯不确定性方法MC Dropout [6] 的结果以供参考。
5.2 经典实验
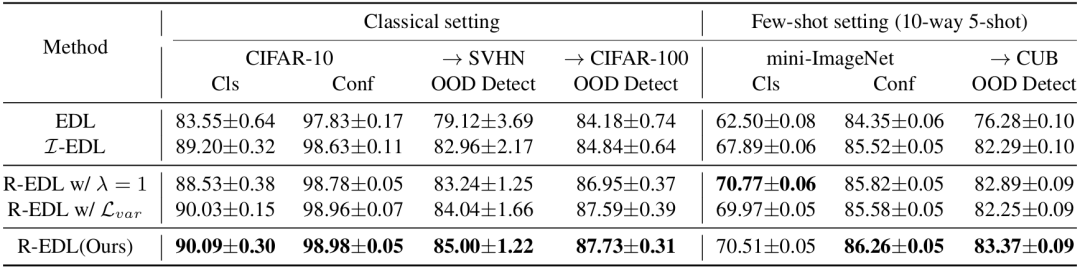
一个具有可靠不确定性估计能力的分类器应该具备以下特征:(1) 对OOD样本赋予比ID样本更高的不确定性;(2) 对误分类样本赋予比正确分类样本更高的不确定性;(3) 保持较高的分类准确性。因此,我们首先通过图像分类中的OOD检测和置信度估计来评估我们的方法,使用精确率-召回率曲线下面积 (AUPR) 作为衡量标准,其中标签为1表示ID/正确分类的数据,标签为0表示OOD/误分类的数据。对于基于狄利克雷的不确定性方法,我们使用最大概率 (MP) 和狄利克雷浓度参数的总和(即主观意见的不确定性质量的缩放倒数 (UM))作为置信度分数。对于MC Dropout和DUQ,我们仅报告它们的MP性能,因为它们不涉及狄利克雷 PDF。正如表1所示,R-EDL方法在大多数指标上都展示了一致的优异性能。特别是,与传统的EDL方法和SOTA方法I-EDL相比,我们的R-EDL在CIFAR-10 vs SVHN的OOD检测设置中,以MP为不确定性时,获得了6.13%和1.74%的性能增益。此外,我们的方法在置信度估计方面也取得了优异的表现,同时保持了令人满意的分类准确性。所有结果均来自5次运行的平均值,R-EDL相对较小的标准差展示了性能的稳定性。
表1 分类准确率、置信度估计和OOD检测的AUPR分数,平均值来自5次运行。在MNIST上,我们采用由3个卷积层和3个全连接层组成的ConvNet作为骨干网络,而在CIFAR-10上,我们采用VGG16。A → B表示将A/B作为ID/OOD数据。MP表示最大概率,UM表示不确定性质量。
5.3 少样本实验
接下来,我们在mini-ImageNet上进行了更具挑战性的少样本实验。如表2所示,我们报告了10,000个少样本实验上的分类平均top-1准确率以及置信度估计和OOD检测的AUPR分数。我们采用N-way K-shot 设置,其中 ,每个实验包含 N 个随机类别,每个类别 K 个随机样本用于训练,从每个类别取
个查询样本用于分类和置信度估计,以及等量来自CUB数据集的查询样本用于OOD检测。正如表 2所示,我们的R-EDL方法在大多数N-way K-shot设置中表现出令人满意的性能。具体来说,与EDL和I-EDL方法相比,我们的R-EDL在5-way 5-shot任务的OOD检测中,以MP为不确定性时,获得了9.19%和1.61%的性能增益。
表2 WideResNet-28-10在mini-ImageNet上的少样本实验结果,使用CUB作为OOD数据,结果为10,000次子实验的平均值。
5.4 抗噪声实验
随后,我们使用噪声数据来评估存在噪声的情况下我们方法的分类鲁棒性和 OOD 检测能力。按照 [22] 的方法,我们通过在 ID 数据集的测试集上引入均值为零的各向同性高斯噪声来生成噪声数据。图1清楚地展示了 R-EDL 在这两个关键指标上的优异表现。
图1 (a) 在不同水平的高斯噪声下,通过分类准确率的平均值和OOD检测的AUPR分数来衡量的EDL、I-EDL和R-EDL的性能趋势。(b) 超参数λ分析,分别通过CIFAR-10上的分类准确率和针对CIFAR-100的OOD检测的AUPR分数进行评估。
5.5消融研究和参数分析
我们评估了在EDL中放宽上述两个非必要设置对性能的影响,如表3所示。特别是,我们探讨了保留原始值 和重新引入被弃用的最小化方差正则化项
的效果。如果恢复这两个原始设置,R-EDL将退化为传统的EDL。正如表3的第3行和第4行所示,恢复任何一个原始设置都会导致显著的性能下降,反之,放宽这些设置则会带来性能提升。例如,在CIFAR-10 vs SVHN的OOD检测中,按AUPR分数衡量,放宽一个设置分别带来了4.12%和4.92%的提升。此外,当两个设置都放宽时,R-EDL的性能提升了5.88%。因此,我们得出结论,这两项放宽都是有效的,并且它们的联合应用可以进一步优化性能。 此外,我们进一步研究了超参数的影响。图1展示了随着超参数从0.01到1.5变化时,CIFAR-10上的分类准确率和CIFAR-100上的OOD检测的AUPR分数的变化趋势。在这种设置中,最终确定为0.1,从[0.1:0.1:1.0]范围内选择,基于验证集上最佳分类准确率进行选择。
表3 保留原始值 和重新引入被弃用的最小化方差正则化项
的消融实验。
06 06. 结论
总结:我们提出了Relaxed-EDL,这是一种EDL的泛化版本,在模型构建和优化阶段放宽了两种传统采用的非必要设置。我们的分析揭示了两个关键发现:(1) 一个常被忽略的参数称为先验权重,它调节了在推导预测分数时利用证据比例和其幅值之间的平衡;(2) 传统EDL方法采用的最小化方差正则项促使狄利克雷PDF逼近狄拉克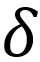
参考文献
- Choi, J., Chun, D., Kim, H., & Lee, H.-J. (2019). Gaussian yolov3: An accurate and fast object detector using localization uncertainty for autonomous driving. Proceedings of the IEEE/CVF International Conference on Computer Vision, 502–511.
- Abdar, M., Khosravi, A., Islam, S. M. S., Acharya, U. R., & Vasilakos, A. V. (2022). The need for quantification of uncertainty in artificial intelligence for clinical data analysis: Increasing the level of trust in the decision-making process. IEEE Systems, Man, and Cybernetics Magazine, 8(3), 28–40.
- Guo, C., Pleiss, G., Sun, Y., & Weinberger, K. Q. (2017). On calibration of modern neural networks. International Conference on Machine Learning, 1321–1330.
- Blundell, C., Cornebise, J., Kavukcuoglu, K., & Wierstra, D. (2015). Weight uncertainty in neural network. International Conference on Machine Learning, 1613–1622.
- Dusenberry, M., Jerfel, G., Wen, Y., Ma, Y., Snoek, J., Heller, K., Lakshminarayanan, B., & Tran, D. (2020). Efficient and scalable bayesian neural nets with rank-1 factors. International Conference on Machine Learning, 2782–2792.
- Gal, Y., & Ghahramani, Z. (2016). Dropout as a bayesian approximation: Representing model uncertainty in deep learning. International Conference on Machine Learning, 1050–1059.
- Lakshminarayanan, B., Pritzel, A., & Blundell, C. (2017). Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in Neural Information Processing Systems, 30.
- Wen, Y., Tran, D., & Ba, J. (2020). Batchensemble: An alternative approach to efficient ensemble and lifelong learning. arXiv Preprint arXiv:2002.06715.
- Egele, R., Maulik, R., Raghavan, K., Lusch, B., Guyon, I., & Balaprakash, P. (2022). Autodeuq: Automated deep ensemble with uncertainty quantification. 2022 26th International Conference on Pattern Recognition (ICPR), 1908–1914.
- Sensoy, M., Kaplan, L., & Kandemir, M. (2018). Evidential deep learning to quantify classification uncertainty. Advances in Neural Information Processing Systems, 31.
- Amini, A., Schwarting, W., Soleimany, A., & Rus, D. (2020). Deep evidential regression. Advances in Neural Information Processing Systems, 33, 14927–14937.
- Bao, W., Yu, Q., & Kong, Y. (2021). Evidential deep learning for open set action recognition. Proceedings of the IEEE/CVF International Conference on Computer Vision, 13349–13358.
- Qin, Y., Peng, D., Peng, X., Wang, X., & Hu, P. (2022). Deep evidential learning with noisy correspondence for cross-modal retrieval. Proceedings of the 30th ACM International Conference on Multimedia, 4948–4956.
- Chen, M., Gao, J., Yang, S., & Xu, C. (2022). Dual-evidential learning for weakly-supervised temporal action localization. European Conference on Computer Vision, 192–208.
- Oh, D., & Shin, B. (2022). Improving evidential deep learning via multi-task learning. Proceedings of the AAAI Conference on Artificial Intelligence, 36, 7895–7903.
- Sun, S., Zhi, S., Heikkilä, J., & Liu, L. (2022). Evidential uncertainty and diversity guided active learning for scene graph generation. The Eleventh International Conference on Learning Representations.
- Park, Y., Choi, W., Kim, S., Han, D.-J., & Moon, J. (2022). Active learning for object detection with evidential deep learning and hierarchical uncertainty aggregation. The Eleventh International Conference on Learning Representations.
- Sapkota, H., & Yu, Q. (2022). Adaptive robust evidential optimization for open set detection from imbalanced data. The Eleventh International Conference on Learning Representations.
- Gao, J., Chen, M., & Xu, C. (2023). Collecting cross-modal presence-absence evidence for weakly-supervised audio-visual event perception. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 18827–18836.
- Jøsang, A. (2001). A logic for uncertain probabilities. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 9(03), 279–311.
- Jøsang, A. (2016). Subjective logic (Vol. 3). Springer.
- Deng, D., Chen, G., Yu, Y., Liu, F., & Heng, P.-A. (2023). Uncertainty estimation by fisher information-based evidential deep learning. arXiv Preprint arXiv:2303.02045.
- Soleimany, A. P., Amini, A., Goldman, S., Rus, D., Bhatia, S. N., & Coley, C. W. (2021). Evidential deep learning for guided molecular property prediction and discovery. ACS Central Science, 7(8), 1356–1367.
- Kandemir, M., Akgül, A., Haussmann, M., & Unal, G. (2022). Evidential turing processes. International Conference on Learning Representations.
- Meinert, N., Gawlikowski, J., & Lavin, A. (2023). The unreasonable effectiveness of deep evidential regression. Proceedings of the AAAI Conference on Artificial Intelligence, 37, 9134–9142.
- Chen, M., Gao, J., & Xu, C. (2023). Cascade evidential learning for open-world weakly-supervised temporal action localization. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 14741–14750.
- Chen, M., Gao, J., & Xu, C. (2023). Uncertainty-aware dual-evidential learning for weakly-supervised temporal action localization. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Gao, J., Chen, M., & Xu, C. (2023). Vectorized evidential learning for weakly-supervised temporal action localization. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Ritter, H., Botev, A., & Barber, D. (2018). A scalable laplace approximation for neural networks. 6th International Conference on Learning Representations, ICLR 2018-Conference Track Proceedings, 6.
- Izmailov, P., Vikram, S., Hoffman, M. D., & Wilson, A. G. G. (2021). What are bayesian neural network posteriors really like? International Conference on Machine Learning, 4629–4640.
- Van Amersfoort, J., Smith, L., Teh, Y. W., & Gal, Y. (2020). Uncertainty estimation using a single deep deterministic neural network. International Conference on Machine Learning, 9690–9700.
- Liu, J., Lin, Z., Padhy, S., Tran, D., Bedrax Weiss, T., & Lakshminarayanan, B. (2020). Simple and principled uncertainty estimation with deterministic deep learning via distance awareness. Advances in Neural Information Processing Systems, 33, 7498–7512.
- Malinin, A., & Gales, M. (2018). Predictive uncertainty estimation via prior networks. Advances in Neural Information Processing Systems, 31.
- Malinin, A., & Gales, M. (2019). Reverse kl-divergence training of prior networks: Improved uncertainty and adversarial robustness. Advances in Neural Information Processing Systems, 32.
- Charpentier, B., Zügner, D., & Günnemann, S. (2020). Posterior network: Uncertainty estimation without ood samples via density-based pseudo-counts. Advances in Neural Information Processing Systems, 33, 1356–1367.
- Bendale, A., & Boult, T. E. (2016). Towards open set deep networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 1563–1572.
- Krishnan, R., Subedar, M., & Tickoo, O. (2018). BAR: Bayesian activity recognition using variational inference. arXiv Preprint arXiv:1811.03305.
- Chen, G., Qiao, L., Shi, Y., Peng, P., Li, J., Huang, T., Pu, S., & Tian, Y. (2020). Learning open set network with discriminative reciprocal points. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part III 16, 507–522.
- McAllester, D. A. (1998). Some pac-bayesian theorems. Proceedings of the Eleventh Annual Conference on Computational Learning Theory, 230–234.
- LeCun, Y. (1998). The MNIST database of handwritten digits. Http://Yann. Lecun. Com/Exdb/Mnist/.
- Xiao, H., Rasul, K., & Vollgraf, R. (2017). Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv Preprint arXiv:1708.07747.
- Clanuwat, T., Bober-Irizar, M., Kitamoto, A., Lamb, A., Yamamoto, K., & Ha, D. (2018). Deep learning for classical japanese literature. arXiv Preprint arXiv:1812.01718.
- Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple layers of features from tiny images.
- Netzer, Y., Wang, T., Coates, A., Bissacco, A., Wu, B., & Ng, A. (2018). The street view house numbers (SVHN) dataset. Technical report, Accessed 2016-08-01.[Online].
- Vinyals, O., Blundell, C., Lillicrap, T., Wierstra, D., et al. (2016). Matching networks for one shot learning. Advances in Neural Information Processing Systems, 29.
- Wah, C., Branson, S., Welinder, P., Perona, P., & Belongie, S. (2011). The caltech-ucsd birds-200-2011 dataset.
- Soomro, K., Zamir, A. R., & Shah, M. (2012). UCF101: A dataset of 101 human actions classes from videos in the wild. arXiv Preprint arXiv:1212.0402.
- Kuehne, H., Jhuang, H., Garrote, E., Poggio, T., & Serre, T. (2011). HMDB: A large video database for human motion recognition. 2011 International Conference on Computer Vision, 2556–2563.
- Monfort, M., Pan, B., Ramakrishnan, K., Andonian, A., McNamara, B. A., Lascelles, A., Fan, Q., Gutfreund, D., Feris, R. S., & Oliva, A. (2021). Multi-moments in time: Learning and interpreting models for multi-action video understanding. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44(12), 9434–9445.
- Simonyan, K., & Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv Preprint arXiv:1409.1556.
- Yang, S., Liu, L., & Xu, M. (2021). Free lunch for few-shot learning: Distribution calibration. arXiv Preprint arXiv:2101.06395.
- Gao, J., Zhang, T., & Xu, C. (2020). Learning to model relationships for zero-shot video classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(10), 3476–3491.

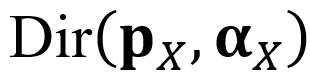 来在主观逻辑的指导下对类概率的分布进行建模,浓度参数由以下公式给出:
来在主观逻辑的指导下对类概率的分布进行建模,浓度参数由以下公式给出: