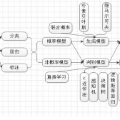
概率语言在几乎所有真实或抽象系统建模的领域中都具有广泛的应用。尽管概率模型具有许多理想特性,例如能够处理不确定性、对全局系统中的边缘变量进行推理以及进行预测,但由于推断的复杂性,这些模型在实践中常常难以使用。因此,研究界开发了多种近似推断方法,以应对越来越复杂的场景。尽管在过去30年里,概率建模和近似推断领域取得了显著进展,但大多数推断方法是以通用实用性为目标开发的,旨在解决广泛类别的概率问题。这也导致了许多针对特定应用设计的概率模型需要同样专门化的推断解决方案,而这些解决方案通常无法在现有文献中找到。本论文研究了结构化场景下的推断问题,与传统方法相比,这些问题包含更复杂的生成假设或数据中的额外信息。对数据结构的考虑通常会引入更难处理的约束,因为在建模和推断过程中必须同时考虑数据间的关系。然而,一旦克服了这些更受限制的推断难题,这些附加信息就可以被有效利用,从而对观察数据得出更精确的结论。在本论文的各章节中,我们探讨了在开发结构化数据的有效概率模型的同时,如何实现高效且有针对性的近似推断。具体而言,我们研究了几种主要的推断方法,包括 马尔可夫链蒙特卡洛(Markov Chain Monte Carlo)、消息传递(message passing)、变分推断(variational inference)以及期望最大化(expectation maximization),并将其应用于超图(hypergraphs)和变分自编码器(variational autoencoders)。在超图场景中,我们展示了如何设计能够考虑数据高阶结构的模型和推断方法;而在变分自编码器场景中,我们提出了理论上有依据的深度学习模型,用于在额外监督和详细生成假设下进行推断。总之,本论文的核心主题是如何在理论和计算上有效利用数据中的附加结构。通过将算法的归纳偏差与数据特性对齐,结构化方法在特定任务上能够超越通用方法,从而从观测中得出更优的结论。