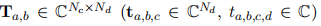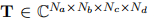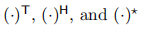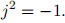摘要

传统上，通信系统物理层的创新是通过将收发器分解成一组处理块来实现的，每个处理块都是基于数学模型独立优化的。这种方法现在受到了对无线连接不断增长的需求以及日益多样化的设备和用例的挑战。相反，基于深度学习（DL）的系统能够处理日益复杂的任务，而这些任务没有可利用的模型。通过从数据中学习，这些系统可以被训练成接受实际硬件和信道的不良影响，而不是试图消除它们。本论文旨在比较不同的方法来释放物理层中DL的全部潜力。

首先，我们描述了一个基于神经网络（NN）的区块策略，其中一个NN被优化以取代通信系统中的一个或多个区块（s）。我们应用这一策略来介绍一个多用户多输入多输出（MU-MIMO）的检测器，它建立在现有的基于DL的架构之上。关键的动机是用一个超网络取代对每个新信道实现的再训练需求，该网络为底层DL检测器生成优化的参数集。其次，我们详细介绍了一个端到端的策略，其中发射器和接收器被建模为NN，被联合训练以最大化可实现的信息速率。这种方法可以进行更深层次的优化，如在满足峰均功率比（PAPR）和相邻信道泄漏比（ACLR）约束的情况下，设计实现高吞吐量的波形。最后，我们提出了一种混合策略，在这种策略中，多个DL组件被插入到一个传统的架构中，但经过训练，以优化端到端的性能。为了证明其优点，我们提出了一个DL增强的MU-MIMO接收器，与传统接收器相比，它既能实现较低的误码率（BER），又能保持对任何用户数量的扩展。

每种方法都有自己的优点和缺点。虽然第一种方法是最容易实现的，但其单独的块状优化并不能确保整体系统的优化性。另一方面，用第二种方法设计的系统在计算上很复杂，不符合目前的标准，但允许出现新的机会，如高维星座和无飞行员传输。最后，即使第三种方法的基于块的结构阻碍了更深层次的优化，但综合的灵活性和端到端的性能收益促使其用于短期的实际实现。

1 简介

1.1 当机器学习遇上信号处理

第一个神经网络（NN）模型于1943年问世[1]，但需要60年的研究和处理能力的提高，才能使机器学习（ML）被业界广泛采用[2]。特别是在2010年代，并行计算有了很大的改进，导致了深度学习（DL）的出现，并在计算机视觉[3]、语音识别[4]和许多其他领域取得了突破[5]-[7]。当手头的任务难以用数学形式化或数学模型无法实现时，DL尤其有用。通过从模型驱动的算法转向数据驱动的算法，只要有足够的数据集，DL技术就能够规避这个问题。通常情况下，由于2009年ImageNet数据集的发布[8]，在图像识别领域取得了巨大的进展，该数据集包含了超过300万张标记的图像。

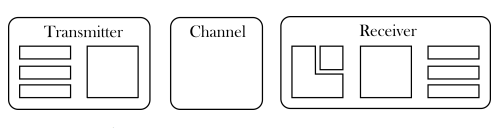
图1.1: 一个传统的基于块的通信系统。

与此同时，从1979年开始，每隔十年就会出现新一代的蜂窝通信系统[9]。每一代都会带来多种连接性的改进，比如更快和更可靠的通信，这部分归功于对无线信道的更好建模。这些数学模型允许设计能够利用信息理论和信号处理方面现有知识的算法。随着发射器和接收器变得越来越复杂，通过将发射和接收处理链分割成小的组件来实现可操作性，通常被称为处理块，如图1.1所示。这种基于块的通信系统有多种缺点。一方面，简单化的信道模型无法捕捉到基础硬件和传播现象的所有特性。另一方面，当推导出更现实的信道模型时，发射器和接收器的联合优化很快就变得难以解决，因此，每个模块的优化通常是独立进行的。这并不能确保所产生的系统的优化性，因为它可以被证明用于信道编码和调制块[10]。最后，在发射器和接收器之间通常需要信号，这引入了一个开销，降低了系统的吞吐量。

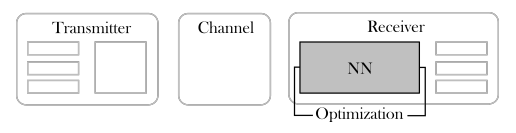
(a) 基于NN的区块优化：一个NN被优化以取代通信系统中的一个或多个区块。

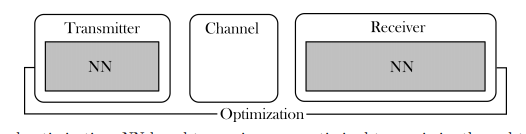
(b) 端对端优化：基于NN的收发器被优化以最大化系统的端到端性能。

图1.2: 将NN集成到通信系统的不同层次。

物理层的DL在九十年代就已经被研究过了[11]，但由于多篇有前途的论文的发表，人们在2016-1017年又开始了新的兴趣。其中一篇是Be'ery等人在2016年发表的，他们将信道解码算法表示为一个NN，以改善使用各种编码的系统的误码率（BER）[12]。这种方法对应于图1.2a所示的基于NN的块优化策略，其中一个或多个连续的处理块被一个NN取代。为了处理这种基于NN的块，下一代通信系统需要为DL设计，其方式是允许对这些组件进行实际训练和测试。虽然这个想法很有趣，但真正的DL革命是从O'Shea和Hoydis在2017年的开创性论文中介绍通信系统的端到端学习开始的[13]。这种方法通常被称为端到端优化策略，如图1.2b所示，Hoydis、Dörner、Cammerer等人用空中传输的方式迅速展示了实验收益[14]。这种策略允许系统完全根据真实世界的数据进行优化，因此能够有效地处理硬件损伤和其他信道失真，而不需要任何数学模型[15]。此外，他们可以通过消除接收器上信道估计所需的引子[16]或学习最佳的媒介访问控制（MAC）协议[17]来帮助减少信令开销。由于这些原因，端到端系统经常被看作是物理层发展的下一个重要步骤，因为发射和接收处理将由DL设计[18]。

对图1.2所示的两种策略的研究，导致发现了DL、信息论和通信系统中的信号处理领域之间的深刻联系[19]。例如，发射器-接收器对可以被建模为一个自动编码器，其中传输比特的估计成为一个二进制分类问题[20]。此外，通信系统的可实现速率可以用交叉熵来表示[21]，它是信息理论和DL中的一个著名指标。这些联系，以及在多个系统和环境上展示的性能改进，表明DL将在未来几代通信系统中发挥重要作用[22]-[24]。然而，每一种策略都有其缺点：基于块的NN（图1.2a）没有经过训练以使系统的整体性能最大化，而完全学习的收发器（图1.2b）缺乏可解释性和可扩展性。因此，本论文旨在为DL组件在无线通信系统中的最佳集成问题提供一些答案。

1.2 当前的挑战和这项工作的贡献

下一代蜂窝网络将需要支持越来越多的不同服务和设备[25]。为此，可用的资源需要在用户之间更有效地共享。一个关键技术是使用多用户多输入多输出（MU-MIMO）系统，利用空间复用来增加信道容量和可同时服务的用户数量[26]。与部署此类系统有关的主要挑战之一是符号检测算法的复杂性，它随着天线和用户数量的增加而增加。例如，最大后验（MAP）检测是最优的，但已知是NP-hard，球体解码器有指数级的最坏情况复杂度[27]。解决这个问题的传统方案是使用线性检测器，这些检测器在计算上是可行的，但在条件不良的信道上会出现性能下降。在过去的几年里，有几种方法试图通过将检测器实现为一个NN来解决这些挑战，这相当于基于NN的块优化策略。然而，它们要么在空间相关的信道上仍然取得不令人满意的性能，要么在计算上要求很高，因为它们需要对每个信道实现进行重新训练。在这项工作中，我们通过训练一个额外的NN（被称为超网络）来解决这两个问题，它将信道矩阵作为输入并生成基于NN的检测器的权重。结果表明，拟议的方法实现了接近最先进的性能，而不需要重新训练。

另一个关键的研究方向是改进正交频分复用（OFDM）波形，该波形用于大多数现代通信系统，如4G、5G和Wi-Fi。事实上，传统的OFDM存在多种缺点，如高峰均功率比（PAPR）和相邻信道泄漏比（ACLR）。为了解决这些问题，我们利用端到端的优化策略，将发射器和接收器建模为NN，分别实现高维调制方案和估计传输比特。然后，我们提出了一种基于学习的方法来设计OFDM波形，以满足选定的约束条件，同时最大限度地提高可实现的信息速率，其额外的优势是在传输过程中不需要试点。通过对ACLR和PAPR目标的评估，可训练的系统能够满足这些约束条件，同时与音调保留（TR）基线相比，能够获得显著的吞吐量。

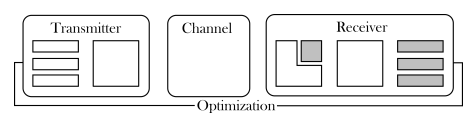
图1.3：一个混合训练策略。

如第1.1节所述，这种端到端系统缺乏可解释性，因为黑盒设计阻止了对信道估计等中间数据的捕获。它们还缺乏可扩展性，这在MU-MIMO传输中尤其重要，因为接收算法必须允许轻松适应不同数量的用户。因此，目前还不清楚这种策略在现实场景中和实际限制下是否比传统的MU-MIMO接收机有竞争力。为此，我们提出了一种DL增强型MU-MIMO接收机，它建立在传统架构的基础上，以保持其可解释性和可扩展性，但被训练成最大化可实现的传输速率。这种方法可以被看作是一种混合策略，即在传统的基于块的架构中插入多个基于DL的组件，但经过优化以最大化端到端的系统性能（图1.3）。由此产生的系统可用于上行和下行链路，并且在训练期间不需要难以获得的完美信道状态信息（CSI），这与现有的工作形成鲜明对比。仿真结果表明，与线性最小均方误差（LMMSE）基线相比，性能有了持续的提高，这在高移动性的情况下尤为明显。

1.3 论文大纲

本论文的其余部分组织如下。第二章介绍了DL、物理层以及这两个领域之间的相互联系的背景。首先介绍了OFDM，并推导了与单输入单输出（SISO）和MU-MIMO传输相应的信道模型。然后，我们详细介绍了反向传播、NN和随机梯度下降（SGD）的概念，并描述了DL增强系统的优化。第三章介绍了基于超网络的MIMO检测器，它是图1.2a中描述的基于块的优化策略的一个例子。介绍了传统的迭代检测框架和超网络的概念，然后描述了HyperMIMO系统和对空间相关信道的评估。第四章讨论了图1.2b的完全基于NN的收发策略，我们设计的OFDM波形既能最大化可实现的速率，又能满足PAPR和ACLR约束。我们描述了系统模型和基线，并详细介绍了用于波形设计的NN架构和基于学习的方法。最后，提供了仿真结果和见解。第五章专门介绍了用于DL增强型MU-MIMO接收机的混合策略（图1.3）。首先，我们开发了对应于上行链路和下行链路传输的传统架构。第二，我们强调了这些架构的两个局限性，并详细说明了我们如何使用卷积神经网络（CNN）来解决这些问题。第三，我们提供了仿真结果，将DL增强的接收器与基线进行比较。最后，第六章是本稿的结论。

1.4 符号

R（C）表示实数（复数）的集合。张量和矩阵用粗体大写字母表示，向量用粗体小写字母表示。我们分别用ma和ma,b表示将矩阵M沿其第一和第二维度切开形成的向量和标量。注意，为了清楚起见，第2.2.2节中也使用了[M]a和[M]a,b的符号。同样，我们用表示将张量沿前两个（三个、四个）维度切片形成的矩阵（向量、标量）。符号T(k)表示手头的数量只考虑第k个用户，而v-a对应的是去除第a个元素的向量v。||M||F表示M的Frobenius规范。Card(S)表示一个集合S中的元素数，vec(-)是矢量化操作符，和分别是元素的乘积和除法。分别表示转置、共轭转置和元素间共轭算子。I(x; y)和P(x, y)分别代表x和y的相互信息和联合条件概率。IN是N×N的身份矩阵，1N×M是N×M的矩阵，其中所有元素都设置为1。最后，虚数单位为j，这样。