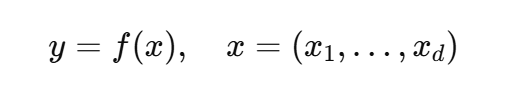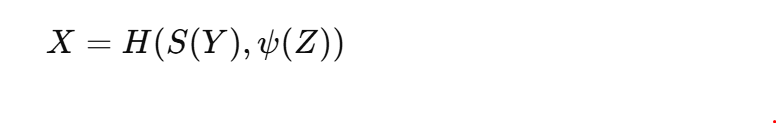生成式建模：综述

生成方法（生成式人工智能，Gen-AI）在解决机器学习和贝叶斯推断任务中的应用进行了综述。生成模型需要模拟一个大规模的训练数据集，并使用深度神经网络来解决监督学习问题。为了实现这一目标，我们需要高维回归方法和用于降维的工具（即特征选择）。生成式人工智能方法的主要优势在于它们能够不依赖具体模型，并利用深度神经网络来估计条件密度或感兴趣的后验分位数。为了说明生成方法的应用，我们分析了著名的埃博拉数据集。最后，我们总结了未来研究的方向。

关键词：生成式人工智能，神经网络，深度学习，ABC，INN，归一化流，扩散模型，分位贝叶斯，拟似推断，埃博拉

1 引言

机器学习中的一个重要任务是：给定输入-输出对，其中输入是高维的，构建一个“查找”表（即字典）来存储输入-输出示例。这是一个编码（即数据压缩问题），用于快速搜索和检索。另一个常见问题是找到一个简单的预测规则（即算法），即：我们能否找到一个好的预测函数f(x)f(x)f(x)，用来在给定xxx 的情况下预测输出yyy？给定一个训练数据集(yi,xi)i=1N(y_i, x_i)_{i=1}^{N}(yi,xi)i=1N 的输入-输出对，我们能否训练一个模型，即找到函数fff？从计算角度来看，我们有一个高维的多变量函数f(x)f(x)f(x)，其中x=(x1,…,xd)x = (x_1, \dots, x_d)x=(x1,…,xd)。 给定(y,x)(y, x)(y,x)-输入-输出对，我们有一个模式匹配（即监督学习）非参数回归形式：

为了实现良好的泛化能力，我们需要能够进行非线性降维，并找到一组合适的特征/因素。关键问题是：我们如何表示一个多变量函数，以便使训练过程高效？许多高维统计模型需要数据降维方法。根据 Breiman（2001），我们将数据表示为由一个黑箱生成，其中输入向量xxx 被黑箱转化为输出yyy，或生成一个描述从xxx 预测yyy 的不确定性的预测分布p(Y∣X)p(Y | X)p(Y∣X)。Fisher（1922）和Cook（2007）清楚地描述了降维问题。虽然通过筛选和将预测值与输出变量绘制来寻找预测器是典型的做法。 统计推断中的一个核心问题是计算一个感兴趣的后验分布。给定似然函数p(y∣θ)p(y | \theta)p(y∣θ) 或前向模型y=f(θ)y = f(\theta)y=f(θ)，以及先验分布π(θ)\pi(\theta)π(θ)，目标是进行逆概率计算，即计算后验分布p(θ∣y)p(\theta | y)p(θ∣y)。对于高维模型来说，这一任务非常困难。马尔科夫链蒙特卡罗（MCMC）方法通过生成后验样本来解决这个问题，使用密度评估。 另一方面，生成式人工智能技术直接学习从均匀分布到目标分布的映射。生成式人工智能的主要优势是它是无模型的，并且不需要使用迭代密度方法。逆贝叶斯映射被通过深度学习的输入输出映射的模式识别所替代。深度分位神经网络（Deep Quantile NNs）提供了一个用于推断决策的通用框架。分位神经网络提供了一种替代不可逆神经网络（如归一化流）的方式。 生成方法通过以下方式解决这两个问题。设Z∼PZZ \sim P_ZZ∼PZ 是潜变量ZZZ 的基础度量，通常是标准多变量正态分布或均匀分布的向量。生成方法的目标是从训练数据(Xi,Yi)i=1N∼PX,Y(X_i, Y_i){i=1}^{N} \sim P{X,Y}(Xi,Yi)i=1N∼PX,Y 中表征后验度量PX∣YP_{X|Y}PX∣Y，其中NNN 被选择为适当的大值。使用深度学习器来估计f^\hat{f}f^，通过非参数回归X=f(Y,Z)X = f(Y, Z)X=f(Y,Z)。深度学习器通过从三元组(Xi,Yi,Zi)i=1N∼PX,Y×PZ(X_i, Y_i, Z_i){i=1}^{N} \sim P{X,Y} \times P_Z(Xi,Yi,Zi)i=1N∼PX,Y×PZ 中学习来估计。随后的估计器H^N\hat{H}NH^N 可以看作是从基础分布到所需后验分布的传输映射。在ZZZ 为均匀分布的情况下，这相当于逆累积分布函数（CDF）采样，即X=FX∣Y−1(U)X = F{X|Y}^{-1}(U)X=FX∣Y−1(U)。 设(X,Y)∼PX,Y(X, Y) \sim P_{X,Y}(X,Y)∼PX,Y 是输入-输出对，且PX,YP_{X,Y}PX,Y 是联合度量，我们可以从中模拟一个训练数据集(Xi,Yi)i=1N∼PX,Y(X_i, Y_i){i=1}^{N} \sim P{X,Y}(Xi,Yi)i=1N∼PX,Y。标准的预测技术是条件后验均值X^(Y)=E(X∣Y)=f(Y)\hat{X}(Y) = E(X|Y) = f(Y)X^(Y)=E(X∣Y)=f(Y)，即给定输出YYY 时预测输入XXX。为此，考虑多变量非参数回归X=f(Y)+ϵX = f(Y) + \epsilonX=f(Y)+ϵ，并提供估计条件均值的方法。通常的估计器f^\hat{f}f^ 包括 KNN 和核方法。最近，提出了深度学习器，并提供了关于仿射函数叠加（即岭函数）的理论属性（见 Montanelli 和 Yang（2020），Schmidt-Hieber（2020），Polson 和 Rockova（2018））。一般来说，我们可以为任何输出YYY 表征后验映射。只需通过使用传输映射：

从新的基础抽样ZZZ 中评估网络。这里，ψ\psiψ 表示余弦嵌入，因此潜变量的架构对应于离散傅里叶近似。另一方面，生成方法通过构建训练数据的“查找”表，并将深度神经网络拟合到该表上，来解决监督学习问题。这提供了一种传输映射到基础分布，基础分布由潜变量zzz 的已知分布p(z)p(z)p(z) 给出。由于我们可以选择样本大小NNN，因此理解这些深度学习估计器的贝叶斯风险属性及其插值属性（称为双重下降）非常重要。 本文的其余部分安排如下：第 1.1 节描述了降维技术；第 2 节介绍了架构设计的多种选择。例如，自动编码器（Albert et al. 2022；Akesson et al. 2021）或隐式模型（参见 Diggle 和 Gratton 1984；Baker et al. 2022；Schultz et al. 2022）；它还与间接推断方法相关（参见 Pastorello et al. 2003；Stroud et al. 2003；Drovandi et al. 2011, 2015）。常用的生成方法包括：变分自动编码器（VAE）、独立成分分析（ICA）、非线性独立成分估计（NICE）、归一化流（NF）、可逆神经网络（INN）、生成对抗网络（GAN）、条件生成对抗网络、近似贝叶斯计算（ABC）和深度拟似推断（DFI）。第 3 节回顾了使用无密度深度分位 ReLU 网络的生成贝叶斯计算（GBC）；第 4 节提供了经典埃博拉数据集的应用。最后，第 5 节总结了未来研究的方向。 深度学习的民间传说：浅层深度学习器能够很好地表示多变量函数，并且在外推时表现良好。因此，我们可以在任何新的输入上评估网络并预测输出，同时我们仍然可以学习感兴趣的后验映射。 双重下降：关于深度神经网络的逼近和插值属性的问题依然存在。最近关于分位神经网络插值属性的研究，参见 Padilla 等（2022）和 Shen 等（2021），Schmidt-Hieber（2020）。另见 Bach（2024）；Belkin 等（2019）。 **

**