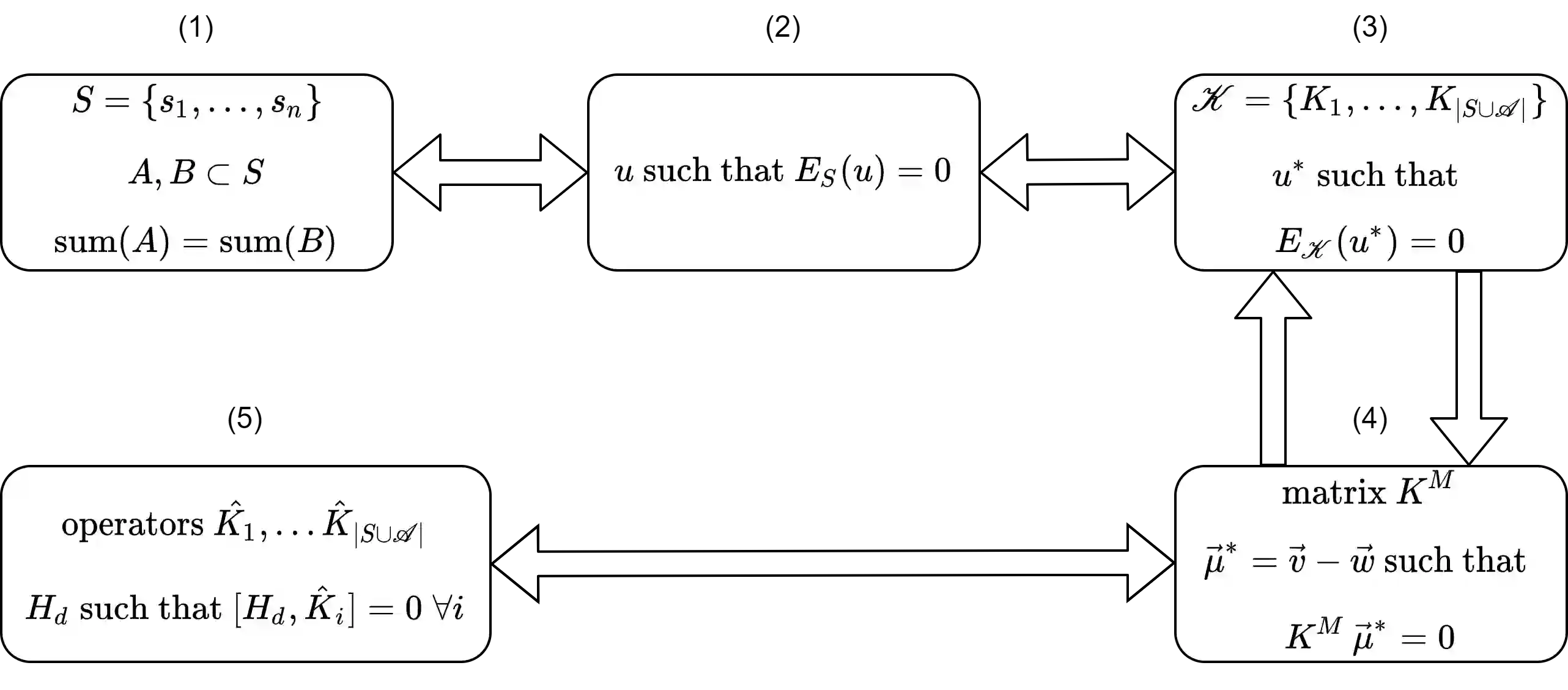
Recent advances in the field of adiabatic quantum computing and the closely related field of quantum annealers has centered around using more advanced and novel Hamiltonian representations to solve optimization problems. One of these advances has centered around the development of driver Hamiltonians that commute with the constraints of an optimization problem - allowing for another avenue to satisfying those constraints instead of imposing penalty terms for each of them. In particular, the approach is able to use sparser connectivity to embed several practical problems on quantum devices than other common practices. However, designing the driver Hamiltonians that successfully commute with several constraints has largely been based on strong intuition for specific problems and with no simple general algorithm to generate them for arbitrary constraints. In this work, we develop a simple and intuitive algebraic framework for reasoning about the commutation of Hamiltonians with linear constraints - one that allows us to classify the complexity of finding a driver Hamiltonian for an arbitrary set of constraints as NP-Complete. Because unitary operators are exponentials of Hermitian operators, these results can also be applied to the construction of mixers in the Quantum Alternating Operator Ansatz (QAOA) framework.
翻译:诊断性量子计算领域的最新进展和量子anners领域密切相关的量子计算领域最近的进展集中在利用更先进和新颖的汉密尔顿式代表来解决优化问题,其中一项进展集中在发展驾驶汉密尔顿人,他们随着优化问题的限制通勤,这为满足这些限制提供了另一条途径,而不是对每一种限制强加惩罚条件;特别是,这种方法能够利用较稀疏的连通性在量子装置上嵌入若干实际问题,而不像其他常见做法那样。然而,设计驾驶员汉密尔顿人成功地通勤,主要基于对具体问题的强烈直觉,没有简单的通用算法来产生任意限制。在这项工作中,我们开发了一个简单和不直观的关于对具有线性限制的汉密尔密尔顿人进行减刑的推理学框架,使我们能够将寻找驾驶员汉密尔顿人作为任意制约的复杂程度归类为NP-Complete。由于统一操作员是赫米蒂安操作员的指数,这些结果也可以应用于Qaant Alterantalatatatatz(QAOAAA)框架的混编。