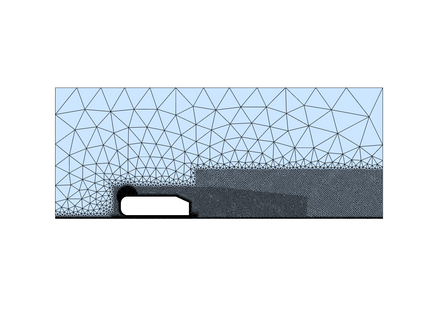
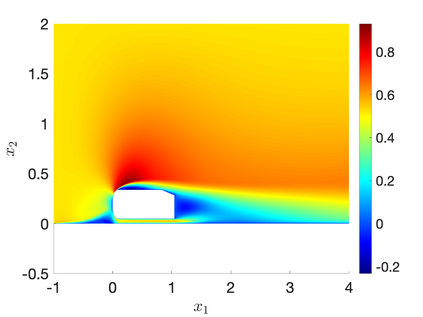
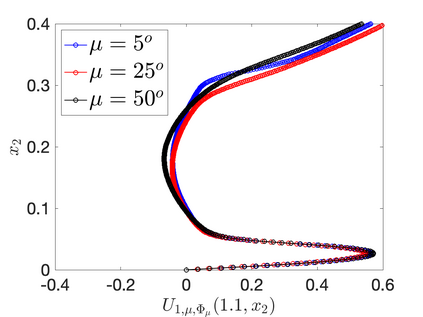
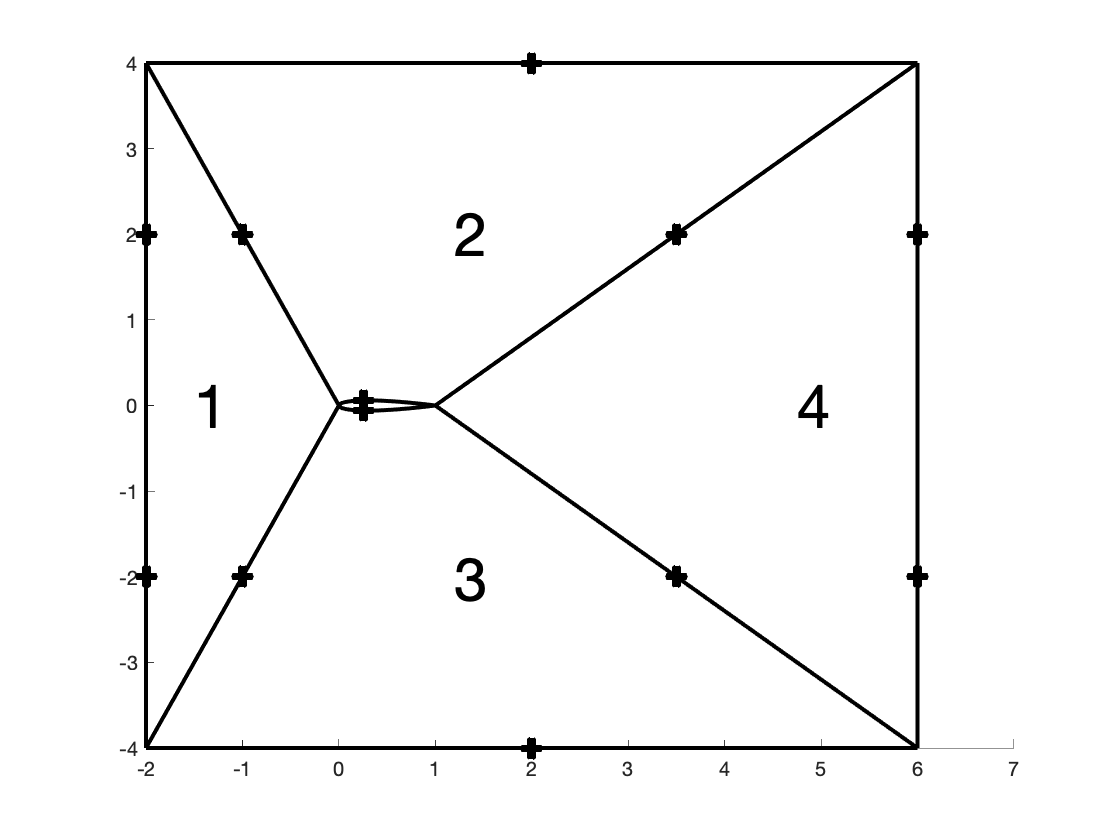
We present a general approach for the treatment of parameterized geometries in projection-based model order reduction. During the offline stage, given (i) a family of parameterized domains $\{ \Omega_{\mu}: \mu \in \mathcal{P} \} \subset \mathbb{R}^D$ where $\mu \in \mathcal{P} \subset \mathbb{R}^P$ denotes a vector of parameters, (ii) a parameterized mapping ${\Phi}_{\mu}$ between a reference domain $\Omega$ and the parameter-dependent domain $\Omega_{\mu}$, and (iii) a finite element triangulation of $\Omega$, we resort to an empirical quadrature procedure to select a subset of the elements of the grid. During the online stage, we first use the mapping to "move" the nodes of the selected elements and then we use standard element-wise residual evaluation routines to evaluate the residual and possibly its Jacobian. We discuss how to devise an online-efficient reduced-order model and we discuss the differences with the more standard "map-then-discretize" approach (e.g., Rozza, Huynh, Patera, ACME, 2007); in particular, we show how the discretize-then-map framework greatly simplifies the implementation of the reduced-order model. We apply our approach to a two-dimensional potential flow problem past a parameterized airfoil, and to the two-dimensional RANS simulations of the flow past the Ahmed body.
翻译:在基于投影的模型排序中,我们提出了一个处理参数化地貌的通用方法。 在离线阶段, 给( 一) 参数化域的组合 $\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \