Gradient Preserving Operator Inference: Data-Driven Reduced-Order Models for Equations with Gradient Structure

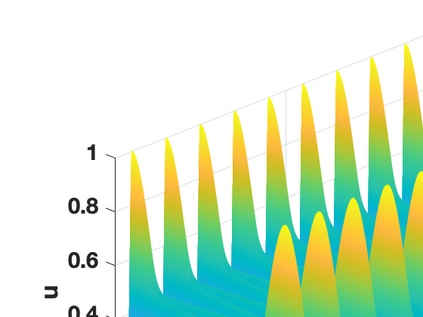
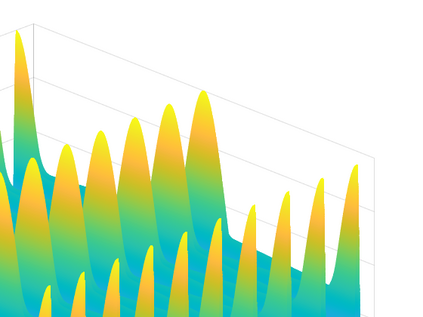
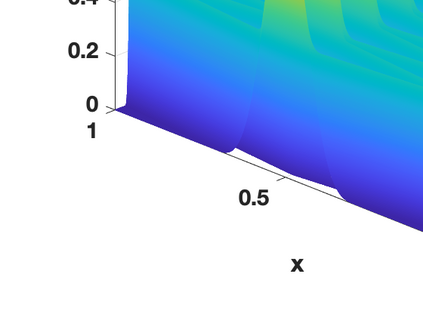
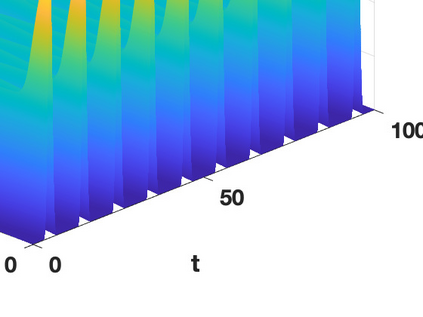
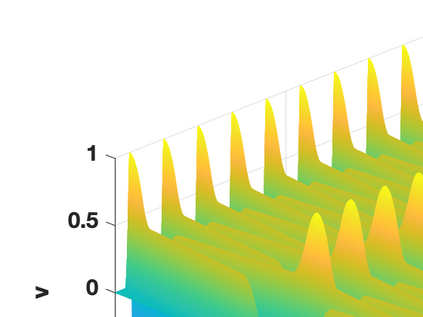
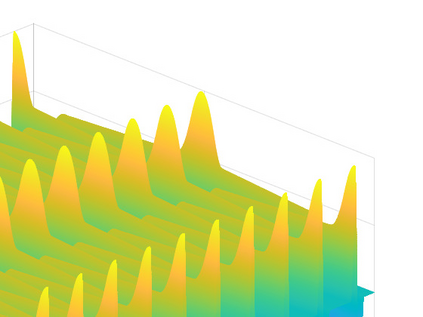
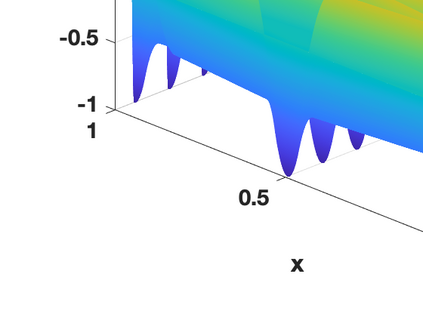
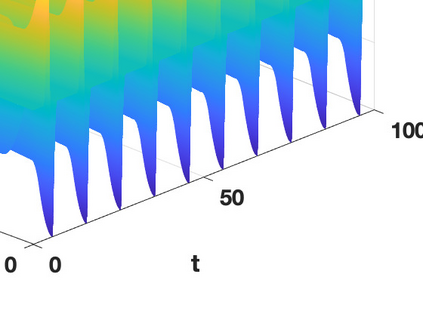
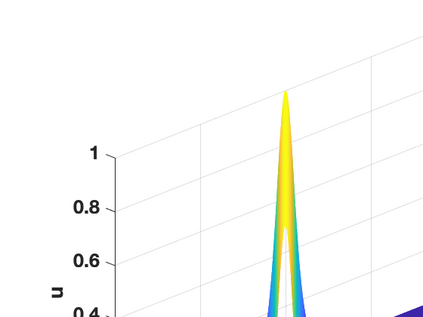
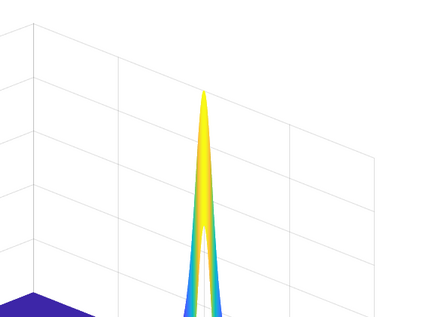
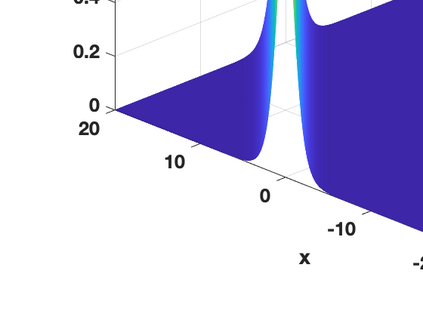
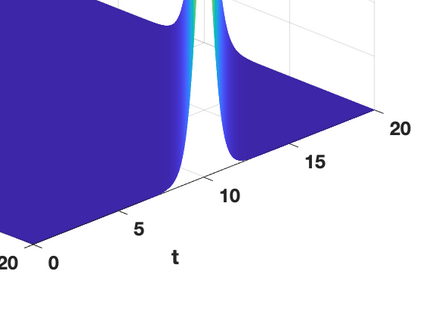
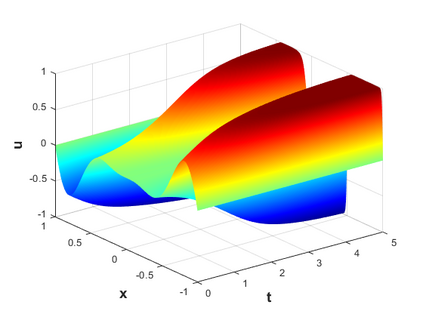
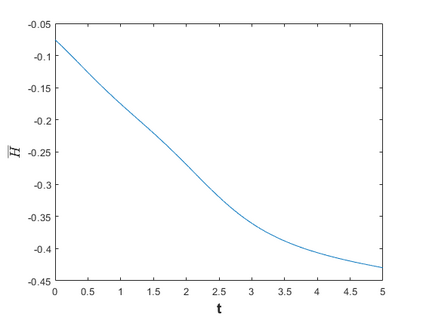
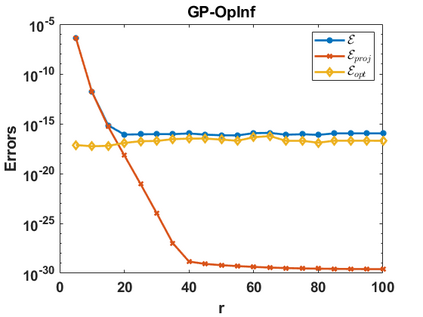
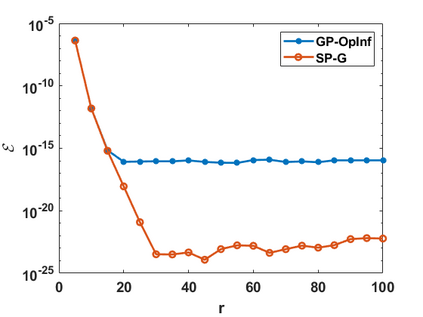
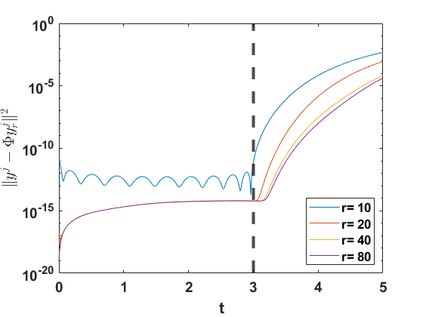
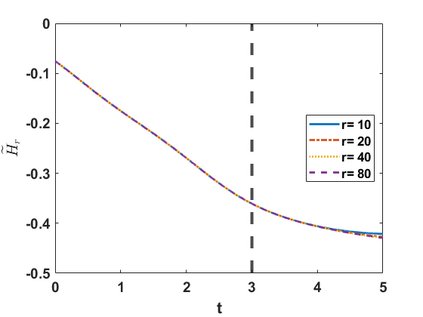
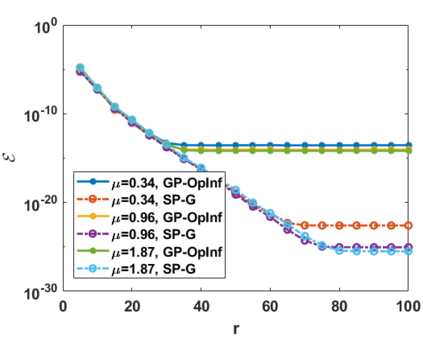
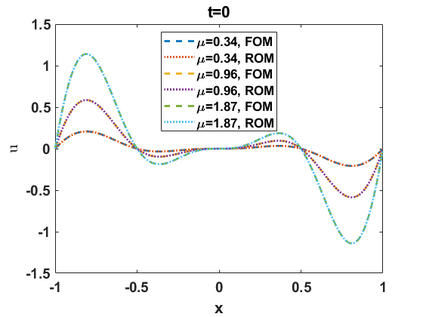
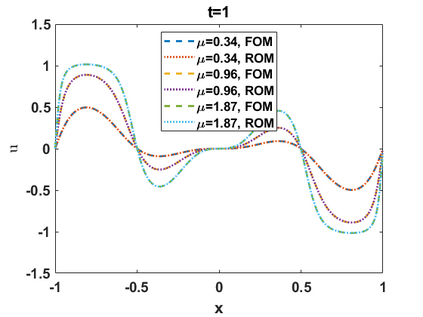
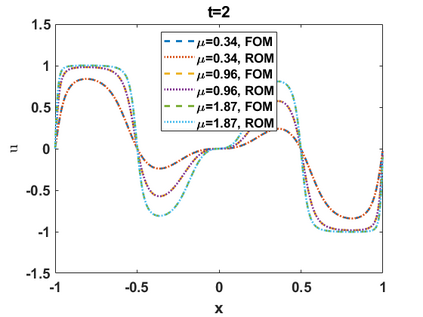
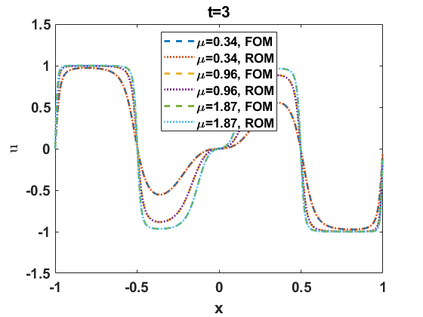
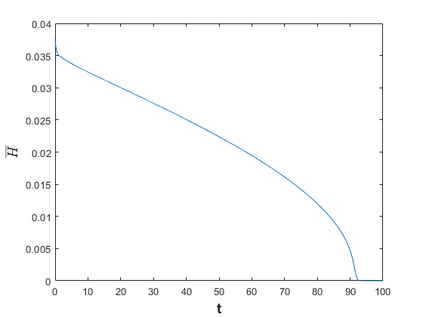
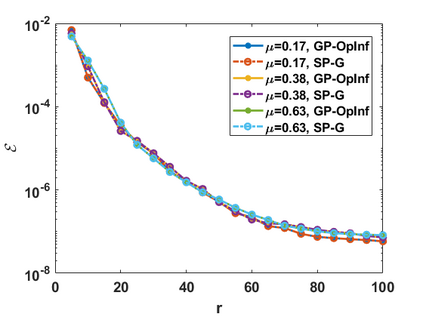
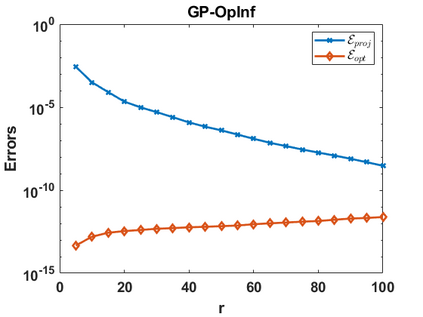
Hamiltonian Operator Inference has been introduced in [Sharma, H., Wang, Z., Kramer, B., Physica D: Nonlinear Phenomena, 431, p.133122, 2022] to learn structure-preserving reduced-order models (ROMs) for Hamiltonian systems. This approach constructs a low-dimensional model using only data and knowledge of the Hamiltonian function. Such ROMs can keep the intrinsic structure of the system, allowing them to capture the physics described by the governing equations. In this work, we extend this approach to more general systems that are either conservative or dissipative in energy, and which possess a gradient structure. We derive the optimization problems for inferring structure-preserving ROMs that preserve the gradient structure. We further derive an {\em a priori} error estimate for the reduced-order approximation. To test the algorithms, we consider semi-discretized partial differential equations with gradient structure, such as the parameterized wave and Korteweg-de-Vries equations in the conservative case and the one- and two-dimensional Allen-Cahn equations in the dissipative case. The numerical results illustrate the accuracy, structure-preservation properties, and predictive capabilities of the gradient-preserving Operator Inference ROMs.