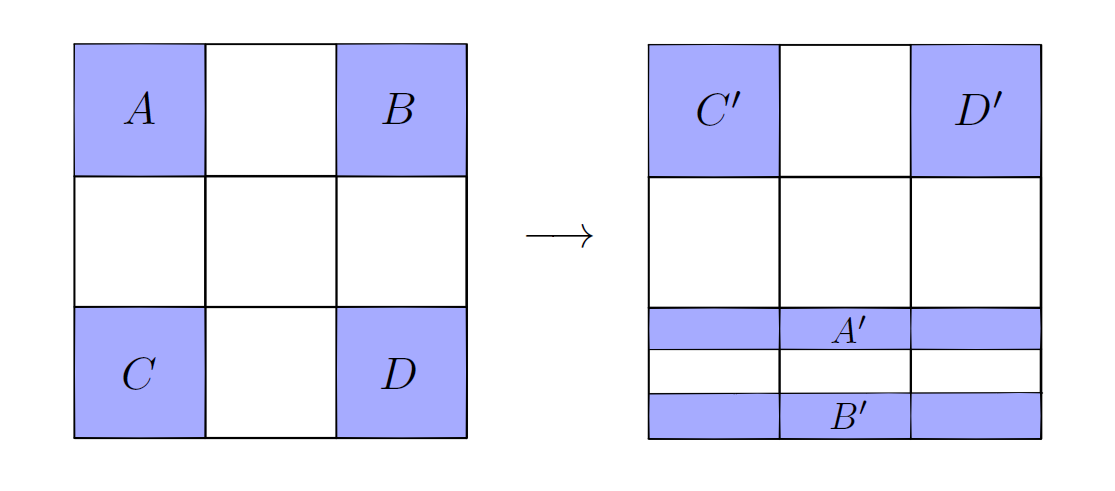
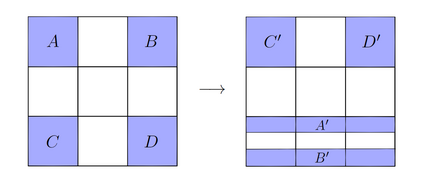
The dynamics of an inviscid and incompressible fluid flow on a Riemannian manifold is governed by the Euler equations. In recent papers [5, 6, 7, 8] several unknown facets of the Euler flows have been discovered, including universality properties of the stationary solutions to the Euler equations. The study of these universality features was suggested by Tao as a novel way to address the problem of global existence for Euler and Navier-Stokes [28]. Universality of the Euler equations was proved in [7] for stationary solutions using a contact mirror which reflects a Beltrami flow as a Reeb vector field. This contact mirror permits the use of advanced geometric techniques in fluid dynamics. On the other hand, motivated by Tao's approach relating Turing machines to Navier-Stokes equations, a Turing complete stationary Euler solution on a Riemannian $3$-dimensional sphere was constructed in [8]. Since the Turing completeness of a vector field can be characterized in terms of the halting problem, which is known to be undecidable [30], a striking consequence of this fact is that a Turing complete Euler flow exhibits undecidable particle paths [8]. In this article, we give a panoramic overview of this fascinating subject, and go one step further in investigating the undecidability of different dynamical properties of Turing complete flows. In particular, we show that variations of [8] allow us to construct a stationary Euler flow of Beltrami type (and, via the contact mirror, a Reeb vector field) for which it is undecidable to determine whether its orbits through an explicit set of points are periodic.
翻译:里格曼方形上隐形和不可压缩流体动态的动态由 Euler 方程式调节。 在最近的论文中, 已经发现了Euler 流的若干未知方面, 包括Euler 方程式的固定解决方案的普遍性属性。 陶先生认为,对这些普遍性特征的研究是解决Euler 和 Navier- Stokes [28] 全球存在问题的一种新颖方法。 在 [7] 中, Euler 方程式的普遍性被证明是用于使用反映 reeb 向量流作为 Reeb 矢量字段的接触镜的固定解决方案。 这个接触镜允许在流中使用先进的几何技术。 另一方面, 由Taor 将图灵机与Navier- Stokes 方程式联系起来的方法所驱动, 在Rietermann 3美元方位上构建了一个完整固定的 Euler 方程式解决方案 [8] 。 由于矢量场的完整性变异性, 可以从一个无法确定的断断裂性问题的角度, 以我们所知道的平流流为无法确定 方向 方向的直径流 直径直径 直径 直径 。 直图的直路的直径直路路的直路的直路的直为直路的直路的直线的直线的直线的直线。 。 。 。 直线的直路的直图的直路的直路的直路的直路的直路的直路的直路的直路的直 直 。 。 直图是否的直的直的直路的直向的直向的直 。 。