Several fitness functions and entanglement gates in quantum kernel generation

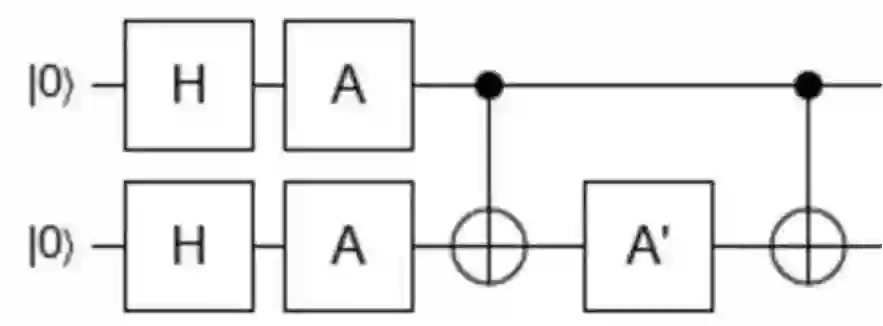
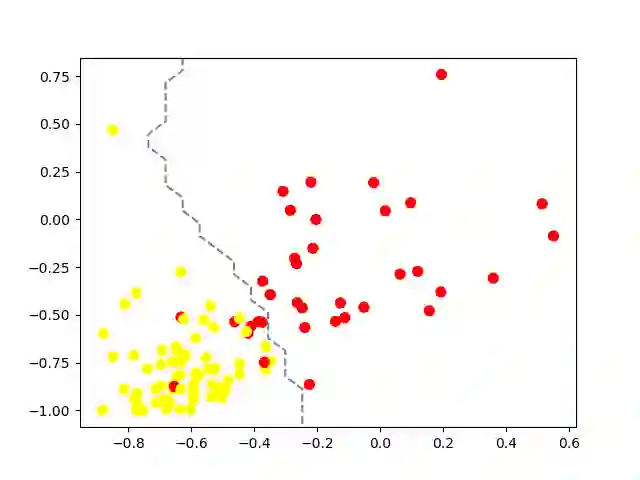
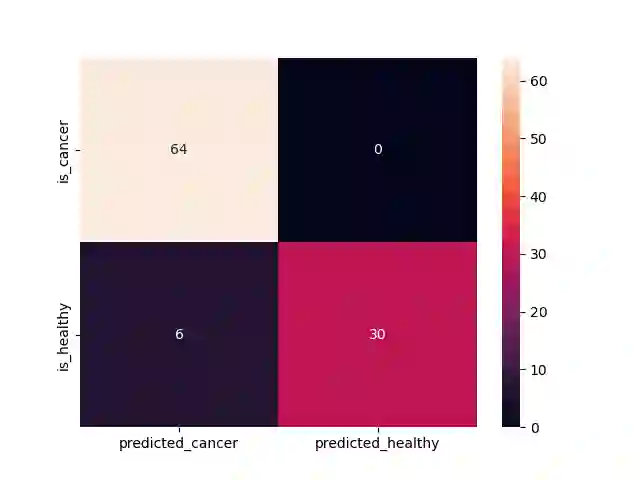
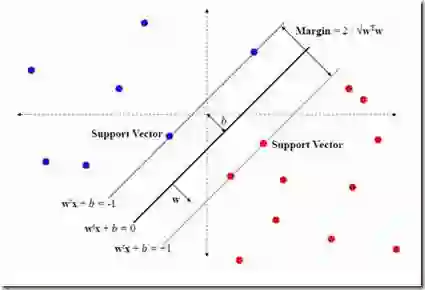
Quantum machine learning (QML) represents a promising frontier in the realm of quantum technologies. In this pursuit of quantum advantage, the quantum kernel method for support vector machine has emerged as a powerful approach. Entanglement, a fundamental concept in quantum mechanics, assumes a central role in quantum computing. In this paper, we study the necessities of entanglement gates in the quantum kernel methods. We present several fitness functions for a multi-objective genetic algorithm that simultaneously maximizes classification accuracy while minimizing both the local and non-local gate costs of the quantum feature map's circuit. We conduct comparisons with classical classifiers to gain insights into the benefits of employing entanglement gates. Surprisingly, our experiments reveal that the optimal configuration of quantum circuits for the quantum kernel method incorporates a proportional number of non-local gates for entanglement, contrary to previous literature where non-local gates were largely suppressed. Furthermore, we demonstrate that the separability indexes of data can be effectively leveraged to determine the number of non-local gates required for the quantum support vector machine's feature maps. This insight can significantly aid in selecting appropriate parameters, such as the entanglement parameter, in various quantum programming packages like https://qiskit.org/ based on data analysis. Our findings offer valuable guidance for enhancing the efficiency and accuracy of quantum machine learning algorithm