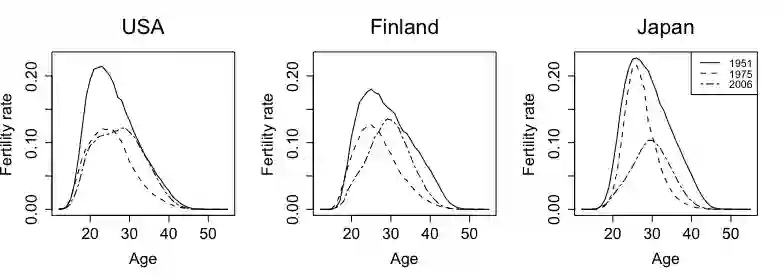
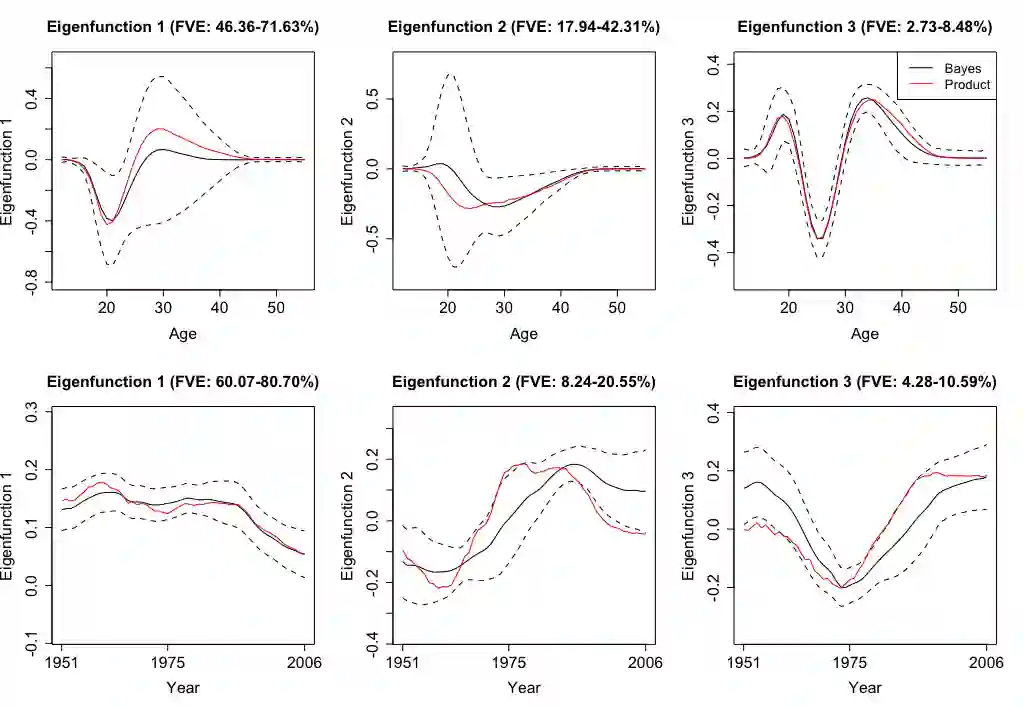
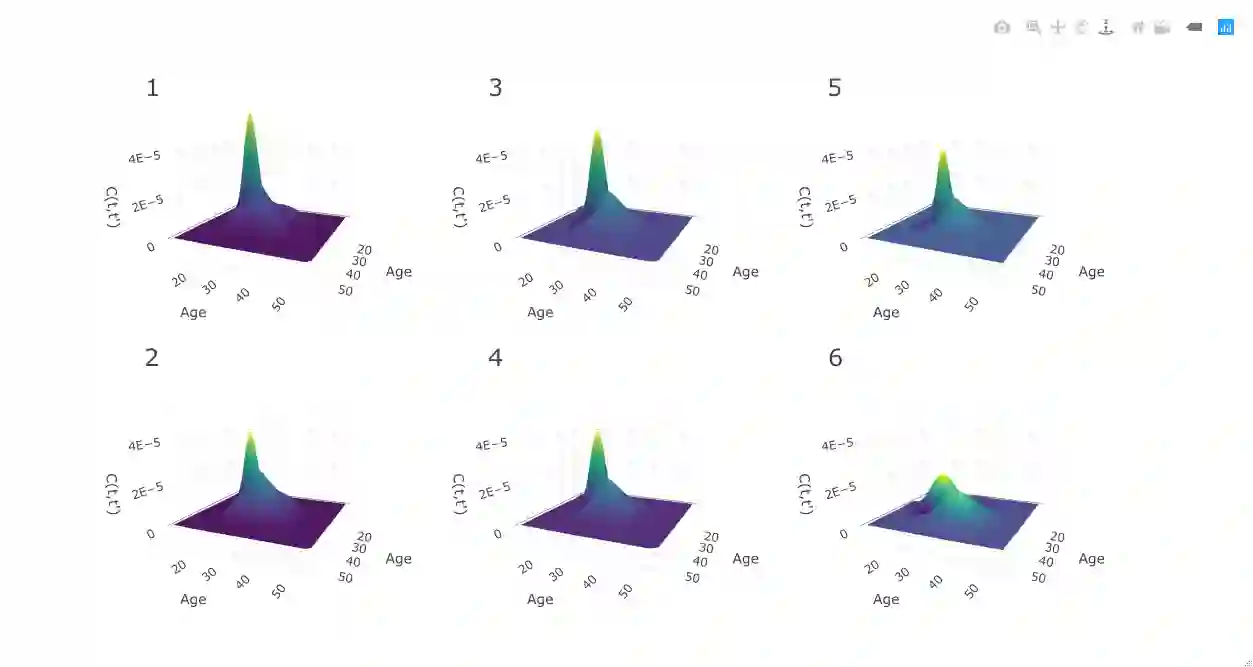
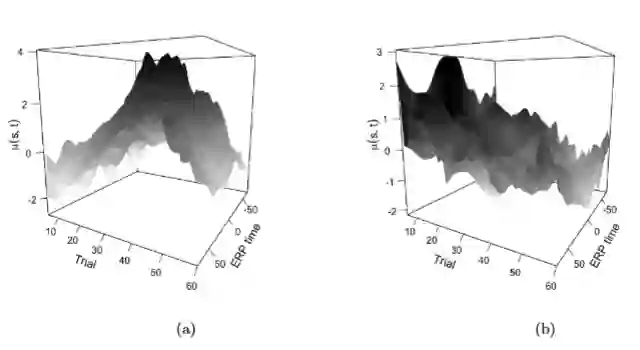
Multi-dimensional functional data arises in numerous modern scientific experimental and observational studies. In this paper we focus on longitudinal functional data, a structured form of multidimensional functional data. Operating within a longitudinal functional framework we aim to capture low dimensional interpretable features. We propose a computationally efficient nonparametric Bayesian method to simultaneously smooth observed data, estimate conditional functional means and functional covariance surfaces. Statistical inference is based on Monte Carlo samples from the posterior measure through adaptive blocked Gibbs sampling. Several operative characteristics associated with the proposed modeling framework are assessed comparatively in a simulated environment. We illustrate the application of our work in two case studies. The first case study involves age-specific fertility collected over time for various countries. The second case study is an implicit learning experiment in children with Autism Spectrum Disorder (ASD).
翻译:在许多现代科学实验和观测研究中产生了多维功能数据。在本文中,我们侧重于纵向功能数据,这是一种结构化的多层面功能数据形式。在纵向功能框架内运作,我们的目标是捕捉低维可解释的特征。我们建议采用一种计算效率的非对称贝叶斯法,以同时平滑观测数据,估计有条件功能手段和功能共差表面。统计推理依据是蒙特卡洛通过适应性阻断的Gibbs抽样从事后测量中采集的样本。在模拟环境中比较评估了与拟议建模框架有关的若干实际特征。我们用两个案例研究来说明我们的工作应用情况。第一个案例研究涉及为不同国家长期收集的按年龄分列的生育率。第二个案例研究是在患有自闭谱障碍的儿童中进行的隐性学习实验。