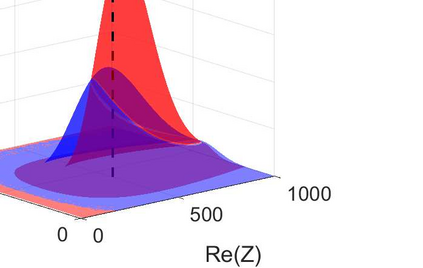
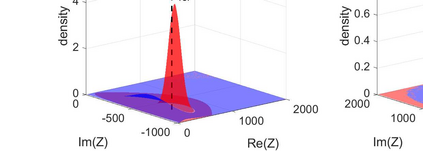
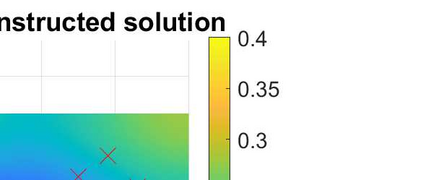
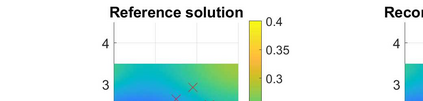
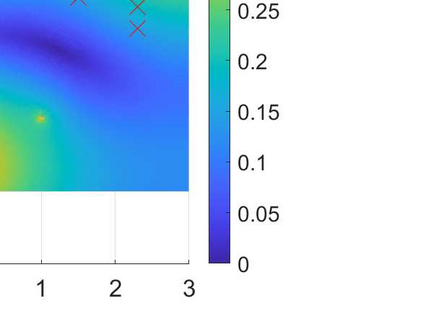
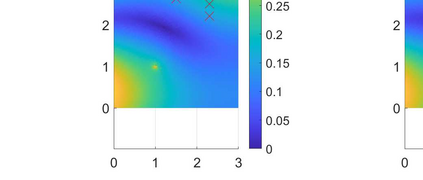
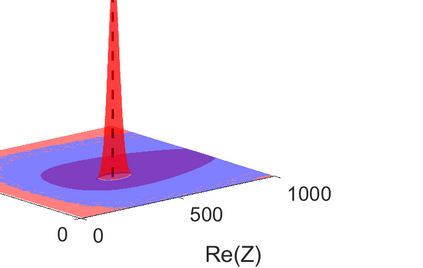
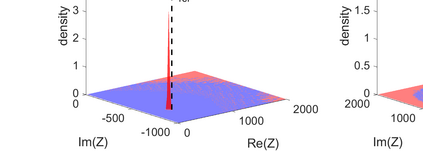
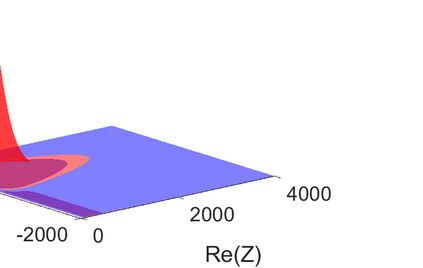
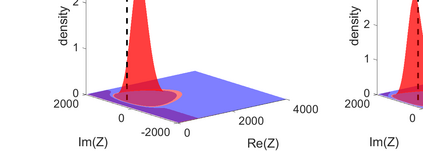
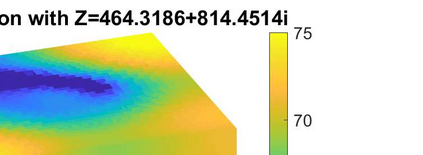
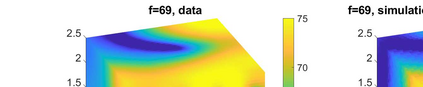
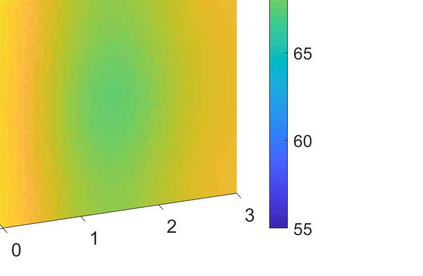
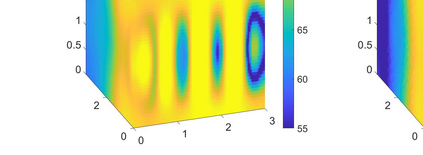
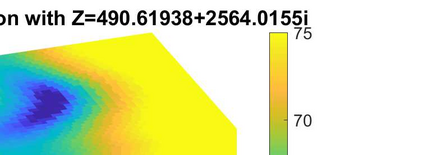
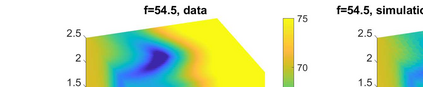
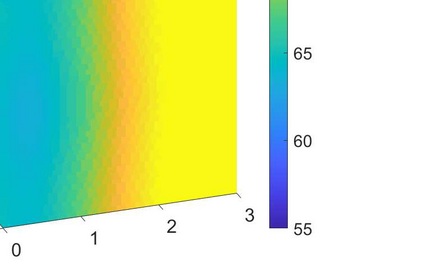
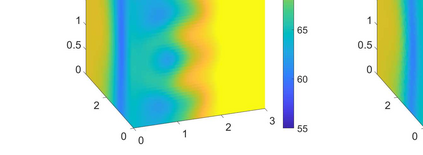
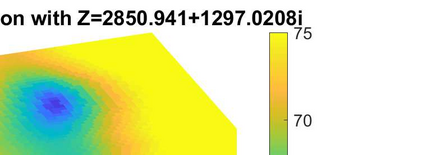
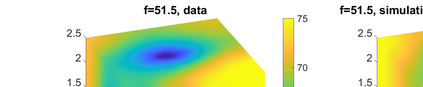
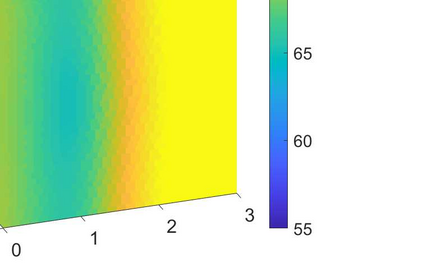
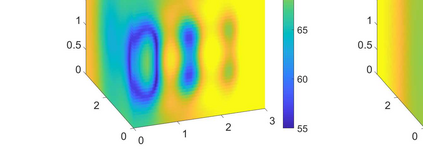
We consider the problem of identifying the acoustic impedance of a wall surface from noisy pressure measurements in a closed room using a Bayesian approach. The room acoustics is modeled by the interior Helmholtz equation with impedance boundary conditions. The aim is to compute moments of the acoustic impedance to estimate a suitable density function of the impedance coefficient. For the computation of moments we use ratio estimators and Monte-Carlo sampling. We consider two different experimental scenarios. In the first scenario, the noisy measurements correspond to a wall modeled by impedance boundary conditions. In this case, the Bayesian algorithm uses a model that is (up to the noise) consistent with the measurements and our algorithm is able to identify acoustic impedance with high accuracy. In the second scenario, the noisy measurements come from a coupled acoustic-structural problem, modeling a wall made of glass, whereas the Bayesian algorithm still uses a model with impedance boundary conditions. In this case, the parameter identification model is inconsistent with the measurements and therefore is not capable to represent them well. Nonetheless, for particular frequency bands the Bayesian algorithm identifies estimates with high likelihood. Outside these frequency bands the algorithm fails. We discuss the results of both examples and possible reasons for the failure of the latter case for particular frequency values.
翻译:暂无翻译