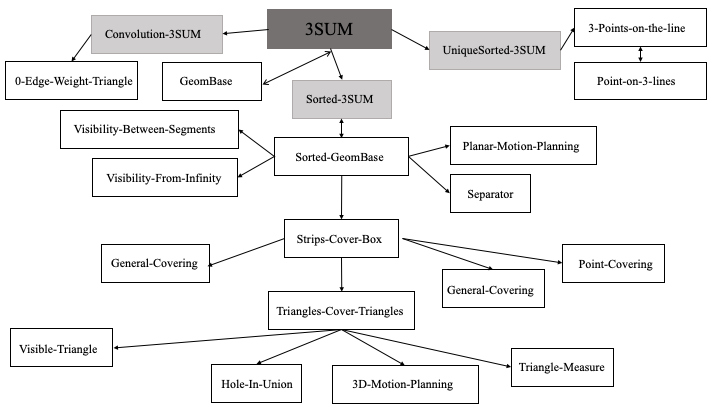
Many computational problems are subject to a quantum speed-up: one might find that a problem having an O(n^3)-time or O(n^2)-time classic algorithm can be solved by a known O(n^1.5)-time or O(n)-time quantum algorithm. The question naturally arises: how much quantum speed-up is possible? The area of fine-grained complexity allows us to prove optimal lower-bounds on the complexity of various computational problems, based on the conjectured hardness of certain natural, well-studied problems. This theory has recently been extended to the quantum setting, in two independent papers by Buhrman, Patro, and Speelman (arXiv:1911.05686), and by Aaronson, Chia, Lin, Wang, and Zhang (arXiv:1911.01973). In this paper, we further extend the theory of fine-grained complexity to the quantum setting. A fundamental conjecture in the classical setting states that the 3SUM problem cannot be solved by (classical) algorithms in time O(n^{2-a}), for any a>0. We formulate an analogous conjecture, the Quantum-3SUM-Conjecture, which states that there exist no sublinear O(n^{1-b})-time quantum algorithms for the 3SUM problem. Based on the Quantum-3SUM-Conjecture, we show new lower-bounds on the time complexity of quantum algorithms for several computational problems. Most of our lower-bounds are optimal, in that they match known upper-bounds, and hence they imply tight limits on the quantum speedup that is possible for these problems.
翻译:许多计算问题都受制于量子加速:人们可能会发现,一个有O(n)3-时间或O(n)2-时间的经典算法的问题可以通过已知的O(n)1.5-时间或O(n)-时间量子算法来解决。 问题自然会产生: 量子加速的可能性有多大? 细微的复杂程度使我们能够根据某些自然和研究周密问题的推测性硬度来证明各种计算问题的复杂性的最佳较低范围。 这个理论最近被扩展至量子设置,由布尔曼、帕特罗和斯佩尔曼(arXiv:1911.05686)编写的两份独立论文和亚伦森、千亚、林、王和张(arXiv:191.01973)编写的两个问题。 在本文中,我们进一步将微量复杂程度理论扩展至量子设置。 古典背景的一个基本猜想指出, 3SUM问题无法通过(cal- listal-ral-ral) 的量法来解决。 在O(n)-n- 3-maryal-ral) 底的调的调调的直径上, 直径上, 直径的直径的直径, 直径是任何的硬质子的硬质问题都显示的硬度的硬度的硬度的硬度, 向。