A heavy-tailed and overdispersed collective risk model

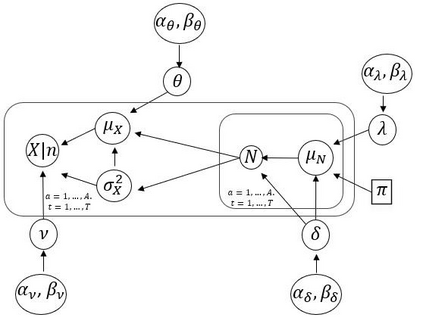
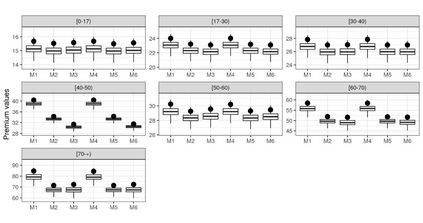
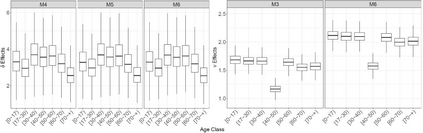
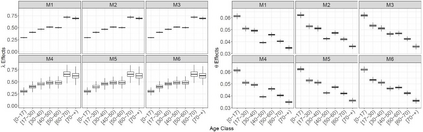
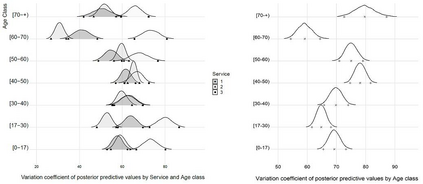
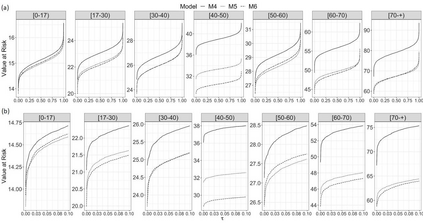
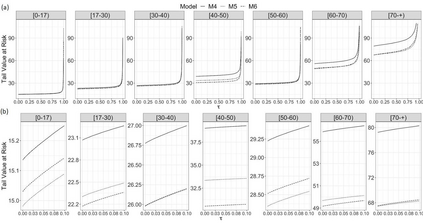
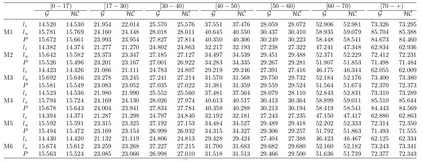
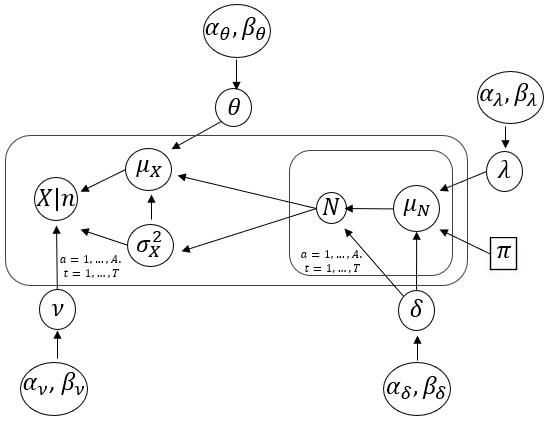
Insurance data can be asymmetric with heavy tails, causing inadequate adjustments of the usually applied models. To deal with this issue, hierarchical models for collective risk with heavy-tails of the claims distributions that take also into account overdispersion of the number of claims are proposed. In particular, the distribution of the logarithm of the aggregate value of claims is assumed to follow a Student-t distribution. Additionally, to incorporate possible overdispersion, the number of claims is modeled as having a negative binomial distribution. Bayesian decision theory is invoked to calculate the fair premium based on the modified absolute deviation utility. An application to a health insurance dataset is presented together with some diagnostic measures to identify excess variability. The variability measures are analyzed using the marginal posterior predictive distribution of the premiums according to some competitive models. Finally, a simulation study is carried out to assess the predictive capability of the model and the adequacy of the Bayesian estimation procedure. Keywords: Continuous ranked probability score (CRPS); decision theory; insurance data; marginal posterior predictive; tail value at risk; value at risk.