Generating synthetic data for neural operators

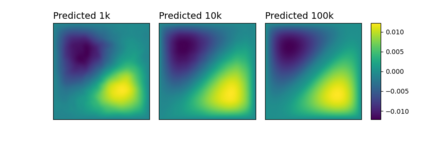
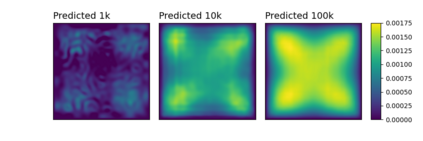
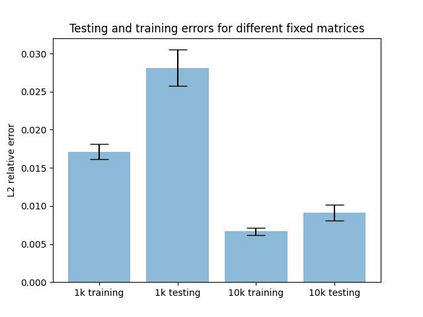
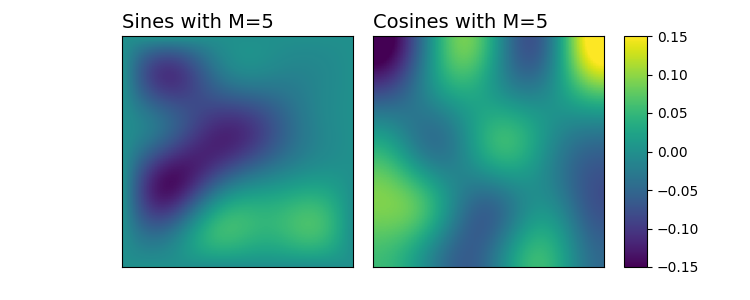
Numerous developments in the recent literature show the promising potential of deep learning in obtaining numerical solutions to partial differential equations (PDEs) beyond the reach of current numerical solvers. However, data-driven neural operators all suffer from the same problem: the data needed to train a network depends on classical numerical solvers such as finite difference or finite element, among others. In this paper, we propose a new approach to generating synthetic functional training data that does not require solving a PDE numerically. The way we do this is simple: we draw a large number $N$ of independent and identically distributed `random functions' $u_j$ from the underlying solution space (e.g., $H_0^1(\Omega)$) in which we know the solution lies according to classical theory. We then plug each such random candidate solution into the equation and get a corresponding right-hand side function $f_j$ for the equation, and consider $(f_j, u_j)_{j=1}^N$ as supervised training data for learning the underlying inverse problem $f \rightarrow u$. This `backwards' approach to generating training data only requires derivative computations, in contrast to standard `forward' approaches, which require a numerical PDE solver, enabling us to generate a large number of such data points quickly and efficiently. While the idea is simple, we hope that this method will expand the potential for developing neural PDE solvers that do not depend on classical numerical solvers.