Quantifying Model Predictive Uncertainty with Perturbation Theory

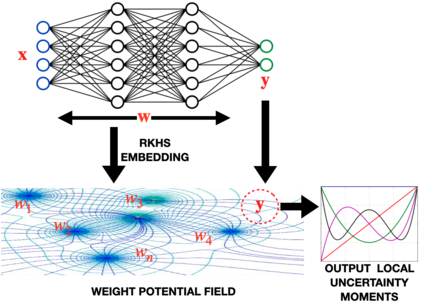
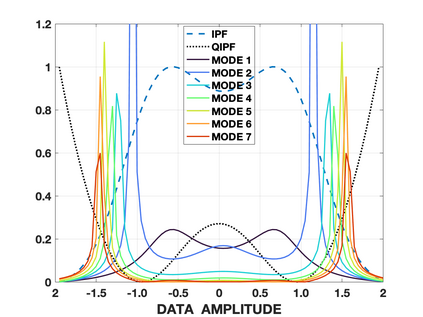
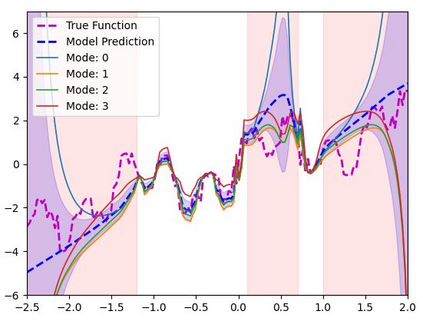
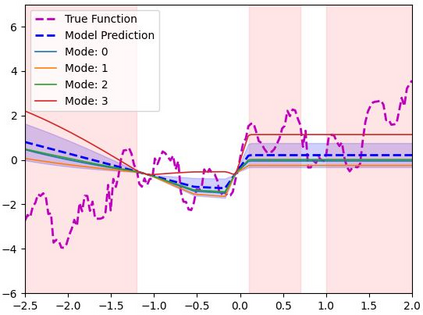
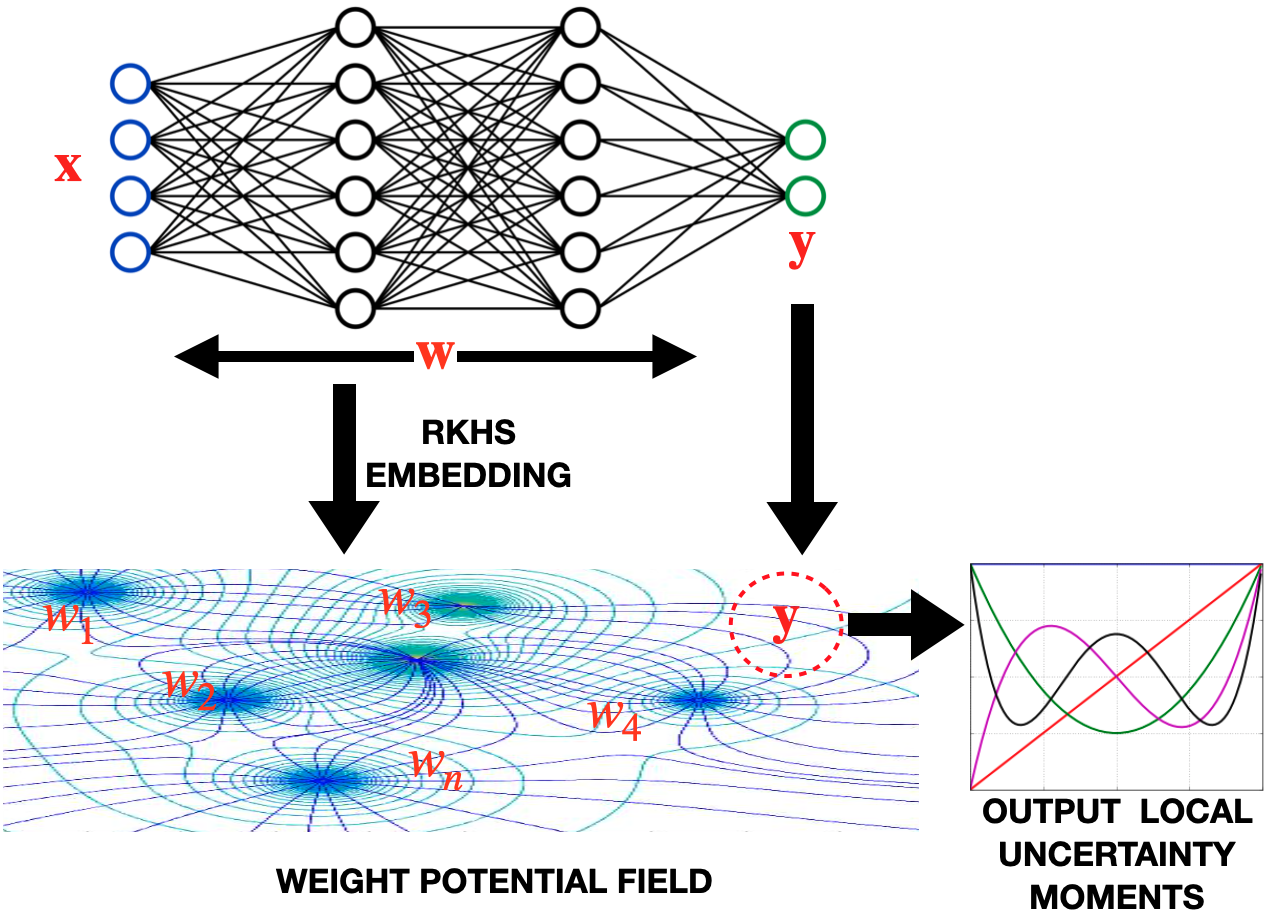
We propose a framework for predictive uncertainty quantification of a neural network that replaces the conventional Bayesian notion of weight probability density function (PDF) with a physics based potential field representation of the model weights in a Gaussian reproducing kernel Hilbert space (RKHS) embedding. This allows us to use perturbation theory from quantum physics to formulate a moment decomposition problem over the model weight-output relationship. The extracted moments reveal successive degrees of regularization of the weight potential field around the local neighborhood of the model output. Such localized moments represent well the PDF tails and provide significantly greater accuracy of the model's predictive uncertainty than the central moments characterized by Bayesian and ensemble methods or their variants. We show that this consequently leads to a better ability to detect false model predictions of test data that has undergone a covariate shift away from the training PDF learned by the model. We evaluate our approach against baseline uncertainty quantification methods on several benchmark datasets that are corrupted using common distortion techniques. Our approach provides fast model predictive uncertainty estimates with much greater precision and calibration.