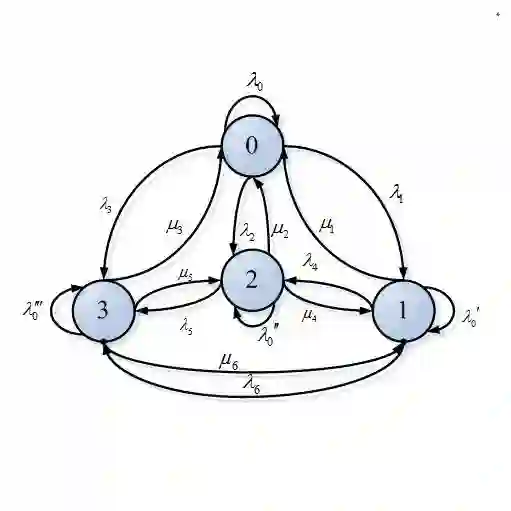
Product-form stationary distributions in Markov chains have been a foundational advance and driving force in our understanding of stochastic systems. In this paper, we introduce a new product-form relationship that we call "graph-based product form". As our first main contribution, we prove that two states of the Markov chain are in graph-based product form if and only if the following two equivalent conditions are satisfied: (i) a cut-based condition, reminiscent of classical results on product-form queueing systems, and (ii) a novel characterization that we call joint-ancestor freeness. The latter characterization allows us in particular to introduce a graph-traversal algorithm that checks product-form relationships for all pairs of states, with time complexity $O(|V|^2 |E|)$, if the Markov chain has a finite transition graph $G = (V, E)$. We then generalize graph-based product form to encompass more complex relationships, which we call "higher-level product form", and we again show these can be identified via a graph-traversal algorithm when the Markov chain has a finite state space. Lastly, we identify several examples from queueing theory that satisfy this product-form relationship.
翻译:马尔可夫链中的乘积形式平稳分布一直是随机系统理解中的基础性进展和驱动力。本文引入一种新的乘积形式关系,我们称之为“基于图的乘积形式”。作为我们的第一个主要贡献,我们证明马尔可夫链的两个状态满足基于图的乘积形式当且仅当以下两个等价条件成立:(i) 基于割的条件,令人联想到乘积形式排队系统中的经典结果;(ii) 我们称为联合祖先自由性的新表征。后一种表征尤其使我们能够引入一种图遍历算法,用于检查所有状态对之间的乘积形式关系,若马尔可夫链具有有限转移图 $G = (V, E)$,其时间复杂度为 $O(|V|^2 |E|)$。随后,我们将基于图的乘积形式推广至更复杂的关系,称之为“高层级乘积形式”,并再次证明当马尔可夫链具有有限状态空间时,这些关系可通过图遍历算法识别。最后,我们从排队论中识别出若干满足此乘积形式关系的实例。